🤵‍♂️ 个人主页: @AI_magician
📡主页地址： 作者简介：CSDN内容合伙人，全栈领域优质创作者。
👨‍💻景愿：旨在于能和更多的热爱计算机的伙伴一起成长！！🐱‍🏍

【深度学习 | 核心概念】那些深度学习路上必经的核心概念，确定不来看看？ （一） 作者： 计算机魔术师 版本： 1.0 （ 2023.8.27 ）

---

摘要： 本系列旨在普及那些深度学习路上必经的核心概念，文章内容都是博主用心学习收集所写，欢迎大家三联支持！本系列会一直更新，核心概念系列会一直更新！欢迎大家订阅

该文章收录专栏
[✨— 《深入解析机器学习：从原理到应用的全面指南》 —✨]

Jaccard相似系数（Jaccard Coefficient）

Jaccard相似系数（Jaccard Coefficient）主要用于计算符号度量或布尔值度量的个体间的相似度（一般用于解决非对称二元的相关性问题），无法衡量差异具体值的大小，只能获得“是否相同”这个结果，所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。Jaccard系数等于样本集交集与样本集合集的比值，可以用于计算两个集合的相似性，无论这些集合是文档、用户的兴趣爱好或任何其他类型的集合。（Tanimoto系数（广义Jaccard相似系数）则可以计算实值）

Jaccard相似系数的定义是，两个集合的交集的大小除以它们的并集的大小。如果记两个集合分别为A和B，交集为A∩B， 并集为A∪B，那么Jaccard相似系数J(A, B)可以表示为：

$$J(A,B)=\frac{|A\cap B|}{|A\cup B|}$$

其中，|A|表示集合A的大小（元素个数）。Jaccard相似系数的取值范围在0到1之间，值越接近1表示两个集合越相似，值越接近0表示两个集合越不相似。

下面我们将详细推导Jaccard相似系数的数学公式：

假设集合A有n个元素，集合B有m个元素，交集A∩B有k个元素。

1. 计算交集的大小 |A∩B|：
   该步骤不需要推导，直接使用给定的数据即可。

2. 计算并集的大小 |A∪B|：
   根据集合的定义，可以得到并集的大小为两个集合的元素个数之和减去交集的大小：
   $$|A\cup B|=|A|+|B|-|A\cap B|=n+m-k$$

3. 计算Jaccard相似系数 J(A, B)：
   将步骤1和步骤2的结果代入公式得到：
   $$J(A,B)=\frac{|A\cap B|}{|A\cup B|}=\frac{k}{n+m-k}$$

我们以二进制数据的列联表举例

计算：假设样本A和样本B是两个n维向量，而且所有维度的取值都是0或1。例如，A（0,1,1,0）和B（1,0,1,1）。我们将样本看成一个集合，1表示集合包含该元素，0表示集合不包含该元素。

q：样本A与B都是1的维度的个数

s：样本A是1而B是0的维度的个数

r：样本A是0而B是1的维度的个数

t：样本A与B都是0的维度的个数

对称二元变量的距离测度:

非对称二元变量的距离测度:

Jaccard系数(非对称二元变量的相似性度量):

即：


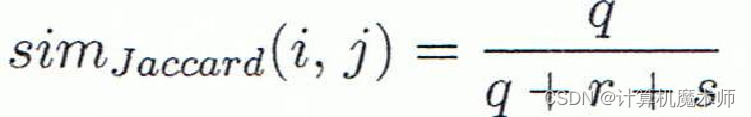
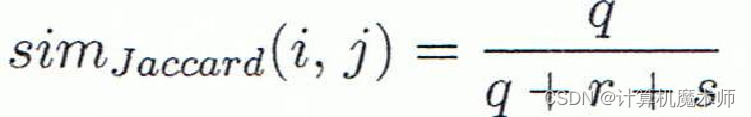
其中我们可以发现$d(i,j)$为相异性 ，$sim(i,j)$为相似性, 符合公式

$1-d（i,j)=sim(i,j)$

以下是一个具体的例子，可以动手算算

接下来，我将给出一个使用Python库（sklearn）加载数据并计算Jaccard相似系数的示例代码：

from sklearn.metrics import jaccard_score

# 定义两个集合的列表表示
A = [1, 2, 3, 4, 5]
B = [4, 5, 6, 7, 8]

# 使用sklearn中的jaccard_score函数计算Jaccard相似系数
jaccard_coefficient = jaccard_score(A, B)

print("Jaccard相似系数:", jaccard_coefficient)

这里使用了sklearn.metrics模块中的jaccard_score函数来计算Jaccard相似系数。输入参数A和B是两个集合的列表表示，函数会返回计算得到的Jaccard相似系数。

此外，如果你想手动实现Jaccard相似系数的计算，以下是一个不使用库的示例代码：

def jaccard_similarity(A, B):
    intersection = len(set(A) & set(B))
    union = len(set(A) | set(B))
    jaccard_coefficient = intersection / union
    return jaccard_coefficient

# 定义两个集合的列表表示
A = [1, 2, 3, 4, 5]
B = [4, 5, 6, 7, 8]

# 计算Jaccard相似系数
jaccard_coefficient = jaccard_similarity(A, B)

print("Jaccard相似系数:", jaccard_coefficient)

这段代码定义了一个名为jaccard_similarity的函数，接受两个集合的列表表示作为参数，并返回Jaccard相似系数的计算结果。

关于Jaccard相似系数的学习资源，你可以参考以下链接-

• Jaccard index - Wikipedia

• Jaccard Similarity and Jaccard Distance

• Measuring Similarity or Dissimilarity Between Sets

						  🤞到这里，如果还有什么疑问🤞
					🎩欢迎私信博主问题哦，博主会尽自己能力为你解答疑惑的！🎩
					 	 🥳如果对你有帮助，你的赞是对博主最大的支持！！🥳