一、点积

        点积的名称源于这个运算符： a•b  在书写点积是的时候中间得原点符合不可省略。计算点积的公式有两种：

点积公式一：对应坐标值相乘相加

        a • b = (aх, ay, az) • (bx, by, bz) = ax * bx + ay * by + az * bz;

点积公式二：矢量模相乘在乘cosθ（θ 为矢量得夹角）

        a • b = |a| |b| cosθ;

点积得几何意义：

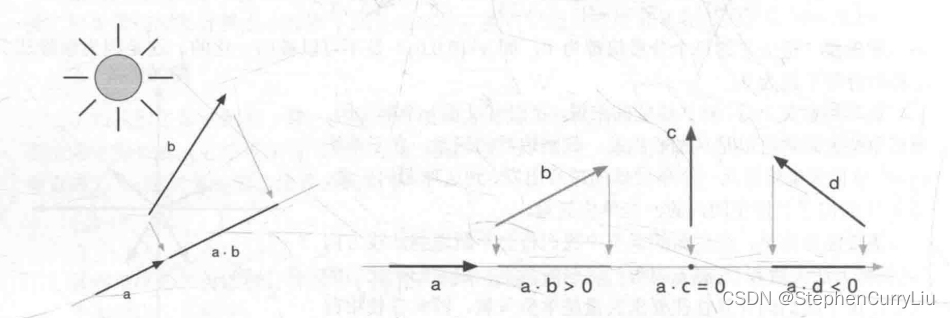
        判断夹角大小：由公式二我们可以分析出，因为矢量的模为矢量的长度肯定大于等于零，所以点积的正负由cosθ决定。

        0⁰ <= θ < 90⁰ : cosθ > 0

        θ  =  90⁰ : cosθ = 0

        90⁰ < θ <= 180⁰ : cosθ < 0

        由此我们可以根据点积的正负值判断夹角的大小：点积为正夹角小于90°、点积等于零夹角等于90°、点积小于零夹角大于90°。

        投影：b 在 a 上面的投影就是 b 头顶点画一条垂直于 a 的线并且相交的点记为 i ，b 尾顶点画一条垂直于a 的线并且相交的点记为 j ，然后求得 i 与 j 之间的距离就为 b 在 a 上面的投影；

由图左一我们可以看出 求b在a的投影就是求b 与  a 夹角的临边 ：

         投影 = |b| cosθ ;

        结合点积公式可得出：

         投影 = |b| cosθ =  a • b / |a| ;

点积的数学性质：

        性质一：点积可结合标量乘法（k 为标量）

        （k * a）• b = a • (k * b) = k * (a • b);

        性质二：点积可以结合矢量加减法

        a • (b + c) = a • b + a • c;

        性质三：矢量和本身进行点积的结果，是该矢量模的平方

        a • a = |a| * |a| * cos0⁰ = |a|⁰

二、叉积

        和点积相同的命名规则，叉积的名称也来源与它的符号：a x b.

        叉积公式：

 a • b = (aх, ay, az) • (bx, by, bz) = (ay * bz - az * by，az * bx -  aх * bz , aх * by - ay * bx )；

 记忆叉积公式非常的困难 我自己发现了一个小规律就是：

        异轴交叉相乘相减  x 在 y 前，y 在 z 前 ，z 在 x 前（相当于x y z 形成了一个圈）。

结合公式看出就是 x 轴的值为其他轴（异轴）的值交叉相乘相减，然后y 在 z 前 所以 x = ay * bz - az * by，同理y轴，z轴也是。

在记忆公式的时候往往理解其中的意思或者自己发现公式的规律自己才会更容易的记忆住。

叉积的几何意义：

        a x b 得到的矢量 c 垂直于 a 与 b 构成的平面。

        而 c 的方向在不同的坐标系下方向也是不同的

        确定一个坐标系如：使用右手坐标系，想象用右手把手心放在a b 尾部交点处，然后展开手掌手掌方向与a的方向重合，在弯曲你的四指指向b，最后伸出你的大拇指，大拇指指的方向就是c的方向。

             

                       

        叉积的主要应用：

        在图像学中判断一个三角面片的朝向

        当确定坐标系是左手还是右手坐标系后 ，a x b = c ，c 的方向就是三角面片在坐标系中的朝向。

        判断一个向量在另一个向量的左侧还是右侧：

        当确定坐标系是左手还是右手坐标系后 ，a x b = c，根据c的方向就可以判断一个向量在另一个向量的左侧还是右侧。当c的方向为正时 b 在 a 的左边，当c的方向为负时 b 在 a 的左边