1. 最小二乘法的基本概念

最小二乘法（又称最小平方法）是一种数学优化技术，它通过最小化误差的平方和来寻找数据的最佳函数匹配。这种方法可以用于求得目标函数的最优值，也可以用于曲线拟合，解决回归问题。利用最小二乘法，可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

最小二乘法的作用主要体现在以下几个方面：

1. 拟合曲线：最小二乘法是解决曲线拟合问题最常用的方法。在已知一组数据点的情况下，可以利用最小二乘法求得一条最能代表这些数据的曲线。
2. 求解未知量：最小二乘法可以用于求解未知量，使得误差值最小。例如，在回归分析中，可以利用最小二乘法求得回归直线的斜率和截距，使得预测值与实际值之间的误差平方和最小。

最小二乘法成立的前提条件是假设系统中无系统误差，误差均为偶然误差，并且假设误差符合正态分布，即整个系统最后的误差均值为零。

2. 最小二乘法的数学公式

最小二乘法的数学公式通常用于线性回归问题，其中目标是找到一条直线（或更高维度的超平面），使得这条直线与给定数据点的误差平方和最小。

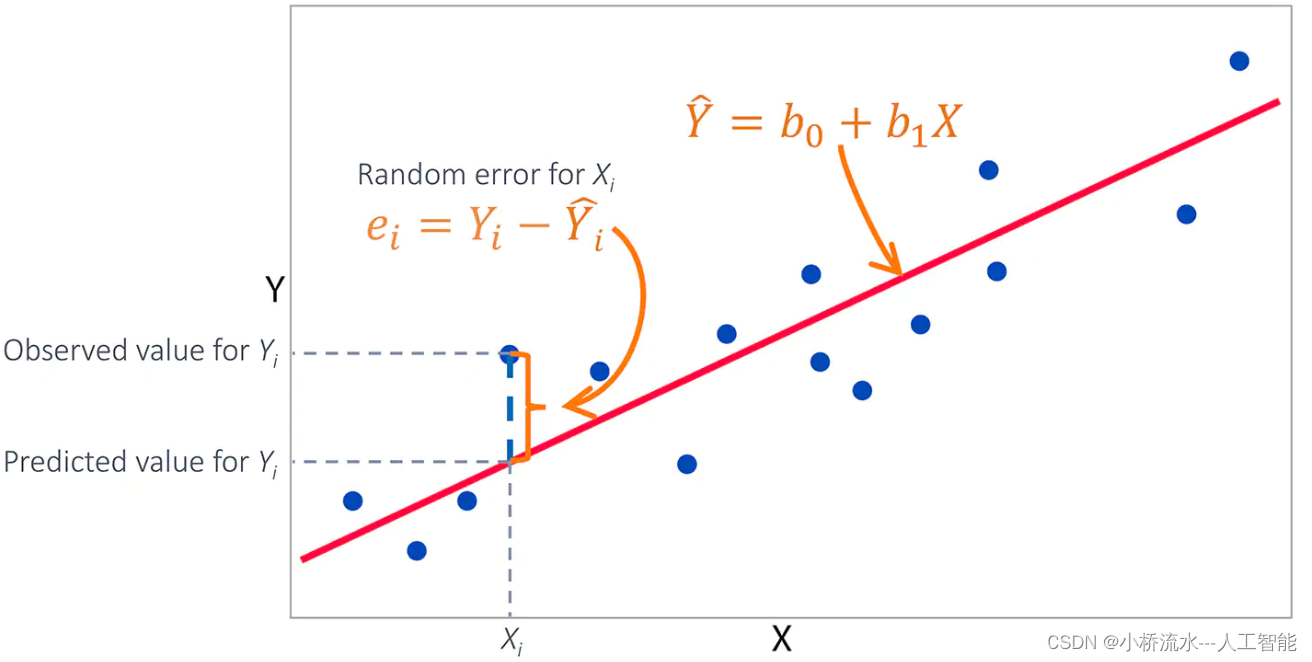
对于一元线性回归，假设有n个数据点 (x_i, y_i)，其中i从1到n。我们的目标是找到一条直线 y = ax + b，其中a是斜率，b是截距。最小二乘法的目标是最小化以下误差平方和：

$$S=\sum _{i=1}^n(y_i-(a{x}_i+b){)}^2$$

为了找到使S最小的a和b的值，我们需要对S求关于a和b的偏导数，并令它们等于零。这样可以得到一个线性方程组，解这个方程组就可以找到最优的a和b。

对于多元线性回归，假设有m个自变量x_1, x_2, …, x_m和一个因变量y。我们的目标是找到一个超平面 y = b_0 + b_1x_1 + b_2x_2 + … + b_m*x_m，其中b_0是截距，b_1到b_m是各个自变量的系数。最小二乘法的目标是最小化以下误差平方和：

$$S=\sum _{i=1}^n(y_i-(b_0+b_1\ast x_{i1}+b_2\ast x_{i2}+...+b_m\ast x_{im}){)}^2$$

同样地，通过求偏导数和令偏导数等于零，我们可以得到一个线性方程组，解这个方程组可以找到最优的b_0, b_1, …, b_m的值。

在实际应用中，我们通常使用线性代数的方法（如矩阵运算）来解这个问题，而不是手动求解偏导数。对于多元线性回归，最小二乘法的解可以通过以下公式得到：

$$\beta =(X^T\ast X{)}^{-1}\ast X^T\ast Y$$

其中，X是数据矩阵，每一行是一个数据点，每一列是一个自变量（包括截距项），Y是观测值向量，β是待求的系数向量。这个公式给出了使误差平方和最小的系数向量β的解析解。

3. 最小二乘法的python例子——使用NumPy

下面是一个使用Python和NumPy库实现简单线性回归的最小二乘法的例子：

import numpy as np

# 假设我们有一组数据点
x_data = np.array([0, 1, 2, 3, 4, 5])
y_data = np.array([0, 0.8, 2.1, 2.9, 4.1, 5.1])

# 为了使用最小二乘法，我们需要构建设计矩阵X
# 在这个例子中，我们有一个截距项和一个斜率项
X = np.vstack([np.ones(len(x_data)), x_data]).T

# 使用NumPy的linalg.lstsq函数来执行最小二乘法
# 这个函数返回四个值：系数、残差、秩和s
coefficients, residuals, rank, s = np.linalg.lstsq(X, y_data, rcond=None)

# 系数数组中的第一个元素是截距，第二个元素是斜率
intercept = coefficients[0]
slope = coefficients[1]

print("Intercept:", intercept)
print("Slope:", slope)

# 使用求得的斜率和截距来生成拟合直线
y_fit = intercept + slope * x_data

# 打印拟合结果
print("Fitted values:", y_fit)

# 可视化原始数据点和拟合直线
import matplotlib.pyplot as plt

plt.scatter(x_data, y_data, label='Original data')
plt.plot(x_data, y_fit, color='red', label='Fitted line')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

在这个例子中，我们首先定义了数据点x_data和y_data，然后构建了一个设计矩阵X，其中包含了一个全为1的列（对应截距项）和x_data本身（对应斜率项）。接着，我们使用np.linalg.lstsq函数执行最小二乘法，得到系数数组coefficients，其中包含了截距和斜率。最后，我们使用这些系数来计算拟合的y值，并将结果可视化。

注意：np.linalg.lstsq函数在NumPy中用于解决最小二乘问题。rcond=None参数用于确定矩阵的秩，通常设置为None让函数自动选择合适的值。这个函数返回的结果中，coefficients是我们需要的系数数组，residuals是残差数组，rank是矩阵的秩，s是奇异值的数组。

4. 最小二乘法的python例子——使用sklearn

使用scikit-learn库可以更方便地执行最小二乘法，因为它提供了高级的接口来处理回归问题。以下是一个使用scikit-learn的LinearRegression类来进行简单线性回归的例子：

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# 假设我们有一组数据点
x_data = np.array([0, 1, 2, 3, 4, 5]).reshape(-1, 1)
y_data = np.array([0, 0.8, 2.1, 2.9, 4.1, 5.1])

# 划分训练集和测试集（在这个简单例子中，我们实际上不需要测试集）
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.2, random_state=42)

# 创建线性回归模型对象
model = LinearRegression()

# 使用训练数据拟合模型
model.fit(x_train, y_train)

# 获取拟合的系数
coefficients = model.coef_
intercept = model.intercept_

print("Coefficients:", coefficients)
print("Intercept:", intercept)

# 使用模型进行预测
y_pred = model.predict(x_data)

# 可视化原始数据点和拟合直线
plt.scatter(x_data, y_data, label='Original data')
plt.plot(x_data, y_pred, color='red', label='Fitted line')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

在这个例子中，我们首先导入了必要的库，然后创建了x_data和y_data数组。我们使用train_test_split函数将数据集划分为训练集和测试集（尽管在这个简单的线性回归例子中，我们实际上不需要测试集来评估模型）。然后，我们创建了一个LinearRegression对象，并使用训练数据调用了fit方法来拟合模型。拟合完成后，我们可以通过coef_和intercept_属性来获取模型的系数和截距。最后，我们使用模型来预测y值，并将原始数据点和拟合的直线可视化。

scikit-learn的LinearRegression类使用了最小二乘法来拟合线性模型，因此你不需要手动实现最小二乘法的数学公式。这使得使用scikit-learn进行回归分析更加简单和高效。