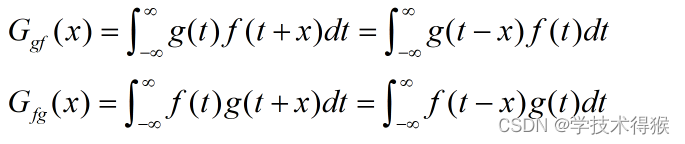
信号与系统——卷积、相关运算与FFT关系以及工程应用(三)
卷积运算、相关运算
一、信号的卷积和相关运算
1.卷积的定义
设有f(x)和g(x)两个函数,如下积分

则称F(x)是f(x)和g(x)的卷积。表示为F(x)=f(x)*g(x)。
2.相关的定义
设有f(x)和g(x)两个函数,如下积分

则称G(x)是f(x)和g(x)相关。
3.卷积与相关的比较
注意观察相关和卷积的定义,则可知:
①卷积运算是某个信号时间反褶后平移到 x点时两个函数重合部分之点积与横坐标轴所包围的面积作为卷积的值,该值是两个函数在x点处重合部分的总体效应,从而将两个函数在 x点处的轮廓平滑或模糊掉
②相关运算中不对信号进行时间反褶,直接对某个信号平移到 x点,然后对另一函数从头到尾进行扫描。反应的是寻求两个函数的相似程度。当f(t )=g(t )时,反映的是自己与自己的相似程度,此时又称为自相关运算。当自相关运算扫描到完全重合时,相似程度达到最大,产生一个峰值。这种相关运算广泛应用于系统的特征识别。
二、卷积与FFT运算
1.线性卷积、循环卷积和周期卷积
1.1 线性卷积
一个长为M的信号x和长为N的系统h进行卷积,相当于在x的前后做N-1个点的padding,然后再与h进行卷积运算,结果的长度为M+N-1,例如fir滤波器,卷积的计算公式也非常简单,对于系统h和输入信号x,卷积的计算公式如下:

与之相关的卷积定理就是DTFT的时域和频域卷积定理

计算方法
被卷积序列x [ n ] 与h [ n ] 的序列长度分别为M 和N,则卷积得到的y [ n ] 序列长为L = M + N − 1 ,计算线性卷积的简单方法为进位保留法

1.2 循环卷积
循环卷积相较于线性卷积区别在于卷积结果的序列长度与被卷积序列长度(输入信号)相同。设序列h ( n )和x ( n )的长度分别为N 和M ,h ( n ) 与x ( n ) 的L 点循环卷积定义为

式中,L 称为循环卷积区间长度,L ≥ m a x [ N , M ],x ( ( n − m ) ) 是以L 为周期的周期信号,N和M的变化区间均是[ 0 , L − 1 ] 。与之相关的卷积定理就是DFT的

由上面公式可知,直接计算比较复杂,通常采用线性卷积或FFT的方法计算循环卷积。最后,如果当循环卷积长度L≥N+M-1时,循环卷积和线性卷积结果一致,因此线性卷积选取合适长度可以利用FFT求解。
1.2.1利用线性卷积计算循环卷积

1.2.2 利用DFT(FFT)计算循环卷积

1.3 周期卷积
周期序列的傅里叶级数(DFS)中提到的,参与运算的是两个周期序列,而且周期都是N

定义式中明显可以看出卷积过程仅限于一个周期内,所以称为周期卷积,卷积的结果也仍然是周期为N的周期序列。周期卷积的结果就是循环卷积结果的周期延拓。与之相关的卷积定理就是DFS的周期卷积定理

2 总结
设卷积序列x [ n ]与h [ n ]的序列长度分别为M 和N,则卷积得到的y [ n ]序列长为L
- 线性卷积和循环卷积的关系
1)当L<N+M-1时,循环卷积是线性卷积长度为L的混叠;
2)当L=N+M-1时,循环卷积=线性卷积;
3)当L>N+M-1时,循环卷积是线性卷积末尾补L-(N+M-1)个零; - 三者之间的关系
1)周期卷积是线性卷积以一定序列长度(设为L)为周期的周期延拓。
2)对周期卷积取主值序列得到循环卷积。
三、相关与FFT运算
从相关运算与卷积的区别与联系可知,相关是不对信号进行时间反褶。如何用FFT计算相关。证明如下。
首先对于一个实信号x(t),那么傅里叶变换具有共轭对称性。也即

所以相关与FFT关系证明如下

因此

只需要利用FFT分别求出G(jw)和F(jw),对G(jw)取共轭G※(jw),再利用FFT反变换即可计算g(t)和f(t)的相关运算。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)