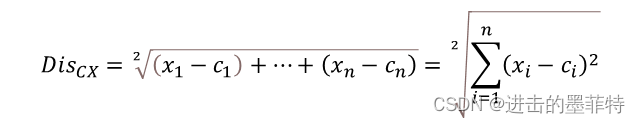
K-Means聚类算法JAVA实现
使用java实现K-Means聚类算法
文章目录
前言
善始者繁多,克终者盖寡。
K-Means是用途极为广泛的聚类算法,因为其操作简单、易于实现的特点,它也是应用最多的算法之一,今天从K-Means算法的原理入手,使用JAVA实现K-Means聚类算法。
一、聚类与分类的区别
聚类算法属于无监督算法,目标类别未知,常见的聚类算法有K-Means、DBSCAN等;
分类算法属于有监督算法,目标类别已知,常见的分类算法有决策树、朴素贝叶斯、支持向量机等。
二、K-Means聚类过程
K-Mean实现步骤如下:
①设定类别数K和聚类迭代次数,在所有样本构成的样本空间中选择K个初始点作为初始聚类中心,初始聚类中心可以是某个样本,也可以为样本空间中的任意点。
②计算所有样本到K个聚类中心的距离,根据距离最小原则将所有样本划分到不同的类别中,样本到聚类中心的距离通常使用欧式距离表示。给定聚类中心C=(c_1, c_2,…, c_n)和样本X=(x_1, x_2,…, x_n),n为样本的属性个数,样本到聚类中心的距离Dis(cx)表示为:

③将初始聚类中所有样本到聚类中心距离的均值作为新的聚类中心,给定某个聚类中样本的集合X=(x_1, x_2,…, x_m),m表示样本个数,其中x_i=(x_i1, x_i2,…, x_in),i表示样本集合中的第i个样本,n表示样本的属性个数,新的聚类中心C可用向量表示为:

④重复步骤②和③,直至各聚类中心不再改变或者达到最大迭代次数。
上述操作看起来很复杂,其实很简单,就是依次计算各样本到聚类中心的距离,把距离小的样本都放在一个类别中,在根据这个类别中的样本计算出新的聚类中心,使用的方法就是求“均值”。
三、JAVA实现
3.1 变量说明
private int k; //聚类数目
private int m; //最大迭代次数
private int dataLength; //数据集中数据的个数
private ArrayList<double[]> data; //数据集
private ArrayList<double[]> center; //聚类中心,结构与各数据点相同
private ArrayList<ArrayList<double[]>> cluster; //聚类形成的簇
private ArrayList<Double> SEE; //聚类中系统整体误差平方和
private int temp; //用于记录最终迭代次数
private ArrayList<double[]> center_copy; //记录初始聚类中心
private int DIMENSION; //记录此次数据点的维度
3.2 构造器与GET/SET方法
根据需要,仅为前6个变量设置GET/SET方法。
//空参构造函数
public MyKmeans(){
}
//包含K值的构造函数
public MyKmeans(int k){
this.k = k;
}
public MyKmeans(int k,int m){
this.k = k;
this.m = m;
}
public int getM() {
return m;
}
public void setM(int m) {
this.m = m;
}
public int getDataLength() {
return dataLength;
}
public void setDataLength(int dataLength) {
this.dataLength = dataLength;
}
public ArrayList<double[]> getData() {
return data;
}
public void setData(ArrayList<double[]> data) {
this.data = data;
}
public ArrayList<double[]> getCenter() {
return center;
}
public void setCenter(ArrayList<double[]> center) {
this.center = center;
}
public ArrayList<ArrayList<double[]>> getCluster() {
return cluster;
}
public void setCluster(ArrayList<ArrayList<double[]>> cluster) {
this.cluster = cluster;
}
3.3 初始化
在系统运行前需对数据集、初始聚类中心、簇等进行初始化,同时还需要对聚类数k和迭代次数m进行检测,聚类数最大不超过数据总个数,最小不低于1。
//初始化聚类,保证程序能够正常运行
public void init(){
// //默认情况下迭代次数为10,参考SPSS,暂未实装
// m=10;
//读取数据文件
readData();
if (data==null || data.size()==0){
//使用系统自带的初始数据集
initData();
}
dataLength = data.size();
//判断K的取值,如果聚类数小于0则设为1类,如果大于数据集中元素个数,则设为dataLength个类
if (k<=0){
k=1;
}
if(k>dataLength){
k=dataLength;
}
//初始化聚类中心,使用随机数实现
initCenter();
//初始化聚类结果,此时聚类结果为K个空的簇
initCluster();
//初始化聚类中的误差平方和
initSEE();
}
3.3.1 初始化数据集
如果为提供数据集,为保证程序正常运行,使用程序默认提供的数据集。
//读取数据文件
public void readData(){
data = new ArrayList<double[]>();
FileInputStream fileInputStream = null;
InputStreamReader inputStreamReader = null;
BufferedReader bufferedReader = null;
try {
fileInputStream = new FileInputStream(new File("./src/data.txt"));
inputStreamReader = new InputStreamReader(fileInputStream);
bufferedReader = new BufferedReader(inputStreamReader);
String str = null;
while ((str = bufferedReader.readLine()) != null){
//获取每一行数据,创建一个一维数组暂时存储这些数据
int len = str.split(",").length;
double[] temp_data = new double[len];
for (int i = 0; i < temp_data.length; i++) {
temp_data[i] = Double.parseDouble(str.split(",")[i]);
}
data.add(temp_data);
DIMENSION = len;
}
} catch (FileNotFoundException e) {
e.printStackTrace();
System.out.println("未找到指定文件!");
} catch (IOException e) {
e.printStackTrace();
System.out.println("打开文件出错!");
}finally {
try {
bufferedReader.close();
} catch (IOException e) {
e.printStackTrace();
}
try {
inputStreamReader.close();
} catch (IOException e) {
e.printStackTrace();
}
try {
fileInputStream.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
//当没有读取本地文件时,使用系统自动的初始数据集,初始数据集为10个二维平面中的点
public void initData(){
DIMENSION = 2;
data = new ArrayList<double[]>();
double[][] default_data = new double[][]{
{0,0},
{1,1},
{2,2},
{3,3},
{4,4},
{5,5},
{6,6},
{7,7},
{8,8},
{9,9}
};
for (int i = 0; i < default_data.length; i++) {
data.add(default_data[i]);
}
}
3.3.2 初始化聚类中心
本人选择从原始数据集中选择初始聚类中心,此方法可能导致初始聚类中心重复!!!
//显示聚类中心
public void show_Cneter(ArrayList<double[]> center){
for (int i = 0; i < center.size(); i++) {
System.out.print("[");
for (int j = 0; j < DIMENSION; j++) {
System.out.print(center.get(i)[j]);
if (j!= DIMENSION-1)
System.out.print(",");
}
System.out.print("]\t");
}
}
//初始化聚类中心,使用随机数生成
public void initCenter(){
center = new ArrayList<double[]>();
for (int i = 0; i <k; i++) {
Random random = new Random();
double[] randoms_center;
//随机指定数据点作为初始中心,可换用其他方法生成随机初始中心
int index = random.nextInt(dataLength);
randoms_center = data.get(index);
center.add(randoms_center);
}
//保存初始聚类中心的副本
//center_copy = center; 此种方法万万不可写
center_copy = new ArrayList<>();
center_copy.addAll(center);
System.out.print("初始聚类中心是:");
show_Cneter(center_copy);
System.out.println();
System.out.println();
}
3.3.3 初始化簇
//初始化聚类结果,此时聚类中包含K个孔的簇
public void initCluster(){
cluster = new ArrayList<>();
for (int i = 0; i < k; i++) {
cluster.add(new ArrayList<>());
}
}
//显示每个簇中的元素
public void show_ClusterData(ArrayList<ArrayList<double[]>> cluster){
for (int i = 0; i < cluster.size(); i++) {
System.out.print("类别"+(i+1)+"包含元素:");
for (int j = 0; j < cluster.get(i).size(); j++) {
System.out.print("[");
for (int index = 0;index < DIMENSION; index++){
System.out.print(cluster.get(i).get(j)[index]);
if (index!= DIMENSION-1)
System.out.print(",");
}
System.out.print("]\t");
}
System.out.println();
}
}
3.3.4 初始化SEE
SEE就是系统的误差,程序停止运行的条件是:
①达到最大迭代次数;
②程序误差不再改变,即SEE的值不再改变。
//初始化聚类中的误差平方和
public void initSEE(){
SEE = new ArrayList<>();
}
3.4 计算两点间距离
/**
* 计算两个点之间的距离
* @param p1 第一个点
* @param p2 第二个点
* @return 两个点见的欧式距离
*/
private double distance(double[] p1,double[] p2){
double result;
double temp_sum = 0.0;
for (int i = 0; i < p1.length; i++) {
temp_sum += (p1[i]-p2[i])*(p1[i]-p2[i]);
}
result = Math.sqrt(temp_sum);
return result;
}
3.5 找到距离最小的聚类中心
//找到当前数据距离聚类中心最小的类别位置
private int minDistance(double[] disstance){
double min_distance = disstance[0];
int min_index = 0;
for (int i = 1; i < disstance.length; i++) {
if (disstance[i]<=min_distance){
min_distance = disstance[i];
min_index = i;
}
}
return min_index;
}
3.6 将数据添加到对应的簇中
根据数据与聚类中心的距离,找到距离最小的聚类中心,将数据加入到该簇中。
//将当前数据元素放到聚类最近的簇中
private void clusterSet(){
double[] dis = new double[k];
System.out.print("此时聚类中心:");
show_Cneter(center);
for (int i = 0; i < data.size(); i++) {
System.out.println();
for (int j = 0; j < k; j++) {
dis[j] = distance(data.get(i),center.get(j));
}
System.out.print("第"+i+"个元素到中心的距离是:");
for (int j = 0; j < dis.length; j++) {
System.out.print(dis[j] + "\t");
}
int location = minDistance(dis);
cluster.get(location).add(data.get(i));
}
System.out.println();
//显示此时簇中包含的元素
show_ClusterData(cluster);
System.out.println();
}
3.7 计算系统SEE
将所有数据放入对应簇后,计算当前系统的SEE值,若此时SEE值与前一次聚类所得SEE值相同,则应结束聚类。
/**
* 求两点之间的误差平方
* @param p1 第一个点
* @param p2 第二个点
* @return 两点之间的误差平方(距离)
*/
private double errorSquare(double[] p1,double[] p2){
double temp_sum = 0.0;
for (int i = 0; i < p1.length; i++) {
temp_sum += (p1[i]-p2[i])*(p1[i]-p2[i]);
}
return temp_sum;
}
//计算当前分类中所有簇中误差平方和
private void countSEE(){
double temp = 0;
for (int i = 0; i < cluster.size(); i++) {
for (int j = 0; j < cluster.get(i).size(); j++) {
//计算当前簇中的所有数据到该簇聚类中心的距离
temp += errorSquare(cluster.get(i).get(j),center.get(i));
}
}
SEE.add(temp);
}
3.8 设置新的聚类中心(最重要操作)
当未达到最大迭代次数或者未收敛时需更新系统聚类中心,以进行下一次聚类。
//设置新的聚类中心,依照以聚类好的各簇中数据求出新的聚类中心
private void setNewCenter(){
// System.out.println("新的聚类中心是:");
for (int i = 0; i < cluster.size(); i++) {
double[] temp_center = new double[DIMENSION];
int n = cluster.get(i).size();
if (n != 0){
for (int j = 0; j < n; j++) {
for (int index = 0; index < DIMENSION; index++) {
temp_center[index] += cluster.get(i).get(j)[index];
}
}
for (int j = 0; j < DIMENSION; j++) {
temp_center[j] = temp_center[j]/n;
}
//将新的聚类中心放入动态数组
center.set(i,temp_center);
}
// System.out.print("["+center.get(i)[0]+","+center.get(i)[1]+"]\t");
}
System.out.println();
}
3.9 迭代
让程序重复执行,直至SEE收敛或达到最大迭代次数
/**
* kmeans算法具体实施步骤
*/
public void kmeans(){
//第一步,初始化各参数
init();
//第二步,执行聚类操作,直到收敛或者到达迭代次数
temp = 1; //用来记录迭代次数
while (true){
//将各数据放入对应簇中
clusterSet();
//计算对应的误差平方好
countSEE();
if (temp > m){
break;
}
if (SEE.size()!=1){
if (SEE.get(temp-1) - SEE.get(temp-2) == 0)
break;
}
//第三步,设置新的聚类中心,重新开始聚类
setNewCenter();
cluster.clear();
initCluster();
//让迭代次数增加
temp++;
}
}
3.10 显示聚类结果
/**
* 显示聚类最终信息
*/
public void show(){
System.out.print("初始聚类中心是:");
show_Cneter(center_copy);
System.out.println();
System.out.print("最终聚类中心:");
show_Cneter(center);
System.out.println();
System.out.println("迭代执行的次数为:"+(temp));
System.out.print("各阶段系统误差平方和");
for (int i = 0; i < SEE.size(); i++) {
System.out.print(SEE.get(i)+"\t");
}
System.out.println();
//显示最后系统中各簇中的元素
show_ClusterData(cluster);
}
四、程序测试
4.1 测试程序
现将聚类数设为4,最大迭代次数为10。
public class MyTest {
public static void main(String[] args) {
MyKmeans myKmeans = new MyKmeans(4, 10);
myKmeans.kmeans();
myKmeans.show();
}
}
4.2 默认数据集
程序第一次操作运行结果为:
 程序最终运行结果为:
程序最终运行结果为:

4.3 其他数据集
程序第一次操作结果为:
 程序最终运行结果为:
程序最终运行结果为:

五、完整代码
整个程序三百多行代码,编写途中可能存在纰漏,还请大家指教!!!
import java.io.*;
import java.util.ArrayList;
import java.util.Random;
public class MyKmeans {
private int k; //聚类数目
private int m; //最大迭代次数
private int dataLength; //数据集中数据的个数
private ArrayList<double[]> data; //数据集
private ArrayList<double[]> center; //聚类中心,结构与各数据点相同
private ArrayList<ArrayList<double[]>> cluster; //聚类形成的簇
private ArrayList<Double> SEE; //聚类中系统整体误差平方和
private int temp; //用于记录最终迭代次数
private ArrayList<double[]> center_copy; //记录初始聚类中心
private int DIMENSION; //记录此次数据点的维度
//空参构造函数
public MyKmeans(){
}
//包含K值的构造函数
public MyKmeans(int k){
this.k = k;
}
public MyKmeans(int k,int m){
this.k = k;
this.m = m;
}
public int getM() {
return m;
}
public void setM(int m) {
this.m = m;
}
public int getDataLength() {
return dataLength;
}
public void setDataLength(int dataLength) {
this.dataLength = dataLength;
}
public ArrayList<double[]> getData() {
return data;
}
public void setData(ArrayList<double[]> data) {
this.data = data;
}
public ArrayList<double[]> getCenter() {
return center;
}
public void setCenter(ArrayList<double[]> center) {
this.center = center;
}
public ArrayList<ArrayList<double[]>> getCluster() {
return cluster;
}
public void setCluster(ArrayList<ArrayList<double[]>> cluster) {
this.cluster = cluster;
}
//初始化聚类,保证程序能够正常运行
public void init(){
// //默认情况下迭代次数为10,参考SPSS,暂未实装
// m=10;
//读取数据文件
readData();
if (data==null || data.size()==0){
//使用系统自带的初始数据集
initData();
}
dataLength = data.size();
//判断K的取值,如果聚类数小于0则设为1类,如果大于数据集中元素个数,则设为dataLength个类
if (k<=0){
k=1;
}
if(k>dataLength){
k=dataLength;
}
//初始化聚类中心,使用随机数实现
initCenter();
//初始化聚类结果,此时聚类结果为K个空的簇
initCluster();
//初始化聚类中的误差平方和
initSEE();
}
//读取数据文件
public void readData(){
data = new ArrayList<double[]>();
FileInputStream fileInputStream = null;
InputStreamReader inputStreamReader = null;
BufferedReader bufferedReader = null;
try {
fileInputStream = new FileInputStream(new File("./src/data.txt"));
inputStreamReader = new InputStreamReader(fileInputStream);
bufferedReader = new BufferedReader(inputStreamReader);
String str = null;
while ((str = bufferedReader.readLine()) != null){
//获取每一行数据,创建一个一维数组暂时存储这些数据
int len = str.split(",").length;
double[] temp_data = new double[len];
for (int i = 0; i < temp_data.length; i++) {
temp_data[i] = Double.parseDouble(str.split(",")[i]);
}
data.add(temp_data);
DIMENSION = len;
}
} catch (FileNotFoundException e) {
e.printStackTrace();
System.out.println("未找到指定文件!");
} catch (IOException e) {
e.printStackTrace();
System.out.println("打开文件出错!");
}finally {
try {
bufferedReader.close();
} catch (IOException e) {
e.printStackTrace();
}
try {
inputStreamReader.close();
} catch (IOException e) {
e.printStackTrace();
}
try {
fileInputStream.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
//当没有读取本地文件时,使用系统自动的初始数据集,初始数据集为10个二维平面中的点
public void initData(){
DIMENSION = 2;
data = new ArrayList<double[]>();
double[][] default_data = new double[][]{
{0,0},
{1,1},
{2,2},
{3,3},
{4,4},
{5,5},
{6,6},
{7,7},
{8,8},
{9,9}
};
for (int i = 0; i < default_data.length; i++) {
data.add(default_data[i]);
}
}
//显示聚类中心
public void show_Cneter(ArrayList<double[]> center){
for (int i = 0; i < center.size(); i++) {
System.out.print("[");
for (int j = 0; j < DIMENSION; j++) {
System.out.print(center.get(i)[j]);
if (j!= DIMENSION-1)
System.out.print(",");
}
System.out.print("]\t");
}
}
//初始化聚类中心,使用随机数生成
public void initCenter(){
center = new ArrayList<double[]>();
for (int i = 0; i <k; i++) {
Random random = new Random();
double[] randoms_center;
//随机指定数据点作为初始中心,可换用其他方法生成随机初始中心
int index = random.nextInt(dataLength);
randoms_center = data.get(index);
center.add(randoms_center);
}
//保存初始聚类中心的副本
//center_copy = center; 此种方法万万不可写
center_copy = new ArrayList<>();
center_copy.addAll(center);
System.out.print("初始聚类中心是:");
show_Cneter(center_copy);
System.out.println();
System.out.println();
}
//初始化聚类结果,此时聚类中包含K个孔的簇
public void initCluster(){
cluster = new ArrayList<>();
for (int i = 0; i < k; i++) {
cluster.add(new ArrayList<>());
}
}
//显示每个簇中的元素
public void show_ClusterData(ArrayList<ArrayList<double[]>> cluster){
for (int i = 0; i < cluster.size(); i++) {
System.out.print("类别"+(i+1)+"包含元素:");
for (int j = 0; j < cluster.get(i).size(); j++) {
System.out.print("[");
for (int index = 0;index < DIMENSION; index++){
System.out.print(cluster.get(i).get(j)[index]);
if (index!= DIMENSION-1)
System.out.print(",");
}
System.out.print("]\t");
}
System.out.println();
}
}
//初始化聚类中的误差平方和
public void initSEE(){
SEE = new ArrayList<>();
}
/**
* 计算两个点之间的距离
* @param p1 第一个点
* @param p2 第二个点
* @return 两个点见的欧式距离
*/
private double distance(double[] p1,double[] p2){
double result;
double temp_sum = 0.0;
for (int i = 0; i < p1.length; i++) {
temp_sum += (p1[i]-p2[i])*(p1[i]-p2[i]);
}
result = Math.sqrt(temp_sum);
return result;
}
//找到当前数据距离聚类中心最小的类别位置
private int minDistance(double[] disstance){
double min_distance = disstance[0];
int min_index = 0;
for (int i = 1; i < disstance.length; i++) {
if (disstance[i]<=min_distance){
min_distance = disstance[i];
min_index = i;
}
}
return min_index;
}
//将当前数据元素放到聚类最近的簇中
private void clusterSet(){
double[] dis = new double[k];
System.out.print("此时聚类中心:");
show_Cneter(center);
for (int i = 0; i < data.size(); i++) {
System.out.println();
for (int j = 0; j < k; j++) {
dis[j] = distance(data.get(i),center.get(j));
}
System.out.print("第"+i+"个元素到中心的距离是:");
for (int j = 0; j < dis.length; j++) {
System.out.print(dis[j] + "\t");
}
int location = minDistance(dis);
cluster.get(location).add(data.get(i));
}
System.out.println();
//显示此时簇中包含的元素
show_ClusterData(cluster);
System.out.println();
}
/**
* 求两点之间的误差平方
* @param p1 第一个点
* @param p2 第二个点
* @return 两点之间的误差平方(距离)
*/
private double errorSquare(double[] p1,double[] p2){
double temp_sum = 0.0;
for (int i = 0; i < p1.length; i++) {
temp_sum += (p1[i]-p2[i])*(p1[i]-p2[i]);
}
return temp_sum;
}
//计算当前分类中所有簇中误差平方和
private void countSEE(){
double temp = 0;
for (int i = 0; i < cluster.size(); i++) {
for (int j = 0; j < cluster.get(i).size(); j++) {
//计算当前簇中的所有数据到该簇聚类中心的距离
temp += errorSquare(cluster.get(i).get(j),center.get(i));
}
}
SEE.add(temp);
}
//设置新的聚类中心,依照以聚类好的各簇中数据求出新的聚类中心
private void setNewCenter(){
// System.out.println("新的聚类中心是:");
for (int i = 0; i < cluster.size(); i++) {
double[] temp_center = new double[DIMENSION];
int n = cluster.get(i).size();
if (n != 0){
for (int j = 0; j < n; j++) {
for (int index = 0; index < DIMENSION; index++) {
temp_center[index] += cluster.get(i).get(j)[index];
}
}
for (int j = 0; j < DIMENSION; j++) {
temp_center[j] = temp_center[j]/n;
}
//将新的聚类中心放入动态数组
center.set(i,temp_center);
}
// System.out.print("["+center.get(i)[0]+","+center.get(i)[1]+"]\t");
}
System.out.println();
}
/**
* 显示聚类最终信息
*/
public void show(){
System.out.print("初始聚类中心是:");
show_Cneter(center_copy);
System.out.println();
System.out.print("最终聚类中心:");
show_Cneter(center);
System.out.println();
System.out.println("迭代执行的次数为:"+(temp));
System.out.print("各阶段系统误差平方和");
for (int i = 0; i < SEE.size(); i++) {
System.out.print(SEE.get(i)+"\t");
}
System.out.println();
//显示最后系统中各簇中的元素
show_ClusterData(cluster);
}
/**
* kmeans算法具体实施步骤
*/
public void kmeans(){
//第一步,初始化各参数
init();
//第二步,执行聚类操作,直到收敛或者到达迭代次数
temp = 1; //用来记录迭代次数
while (true){
//将各数据放入对应簇中
clusterSet();
//计算对应的误差平方好
countSEE();
if (temp > m){
break;
}
if (SEE.size()!=1){
if (SEE.get(temp-1) - SEE.get(temp-2) == 0)
break;
}
//第三步,设置新的聚类中心,重新开始聚类
setNewCenter();
cluster.clear();
initCluster();
//让迭代次数增加
temp++;
}
}
}

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容





所有评论(0)