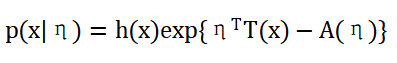
广义线性回归(GLM)
广义线性回归与指数分布族
文章目录
一、前言
我们在学习逻辑回归的时候,通常会看到一句话:“逻辑回归是一种广义线性模型”。有些同学可能不太了解这句话的含义,那么本文的主要目的就是通俗的解读一下什么是广义线性模型以及求解相应激活函数、损失函数?
二、什么是广义线性模型(GLM)
大家都知道,线性回归模型就是通过数据去拟合出一条直线,其公式可以写成如下形式:

其中,Z为回归值,即输出;W为参数矩阵(即我们所估计的参数);X为输入数据;b为截距(偏置)。
二分类逻辑回归就是在线性回归的基础上,通过sigmoid函数对线性回归的输出Z进行映射,使映射后的数据符合伯努利分布,即输出值从连续值z,变为g(z),其值仅为0和1。

说到这里,大家可能已经大致明白了,广义线性回归,其实就是通过某个激活函数,将线性回归的输出值映射成不同的分布,比如说伯努利分布、泊松分布、伽马分布等。不同的分布对应不同的激活函数,并且通过不同的损失函数进行迭代训练,从而得到不同应用场景下的广义线性回归模型(可以根据目标值的分布情况选择不同的模型)。
三、指数分布族
上面提到的激活函数和损失函数都可以通过指数分布族来描述,对于广义线性回归模型来说,指数分布族就是其内核,其公式如下(各种资料书写形式可能不一样,可自行进行相关变换):

其中:
η:参数,一般为向量;
A(η):log配分函数,与x无关;
h(x):关于x的函数,与η无关,也可以为常数;
T(x):充分统计量,代表样本的分布情况(均值,方差等),包含样本的所有信息。
对于指数分布族,存在如下性质,具体证明可参考本视频:


接下来我们将高斯分布、伯努利分布等概率公式转换成指数分布族的形式,从而得出上面提到各种概率分布的激活函数。
3.1 高斯分布(Gaussian)
高斯分布,即正态分布,其概率密度函数如下:

其指数分布族形式为:

参照指数分布族形式,可以得出:

注:高斯分布有两个参数,因此自然参数以及充分统计量都有两个。此时A(η)对η1求一阶、二阶导,即为x的均值和方差。
3.2 伯努利分布(Bernoulli)
伯努利分布,其概率密度函数如下:

其指数分布族形式为:

参照指数分布族形式,可以得出:

3.3 泊松分布(Poisson)
泊松分布,其概率密度函数如下:

其指数分布族形式为:

参照指数分布族形式,可以得出:

3.4 伽马分布(gamma)
伽马分布,其概率密度函数如下:

其中,分母部分为伽马函数,即:

伽马分布也可以写成如下形式:

其指数分布族形式为:

参照指数分布族形式,可以得出:

四、激活函数求解
第三节中我们已经知道,在广义线性模型中,为了提高可操作性,概率密度函数必须符合指数分布族的形式,即:

其中η即为回归模型输出的连续值,即:

η也是激活函数的输入,即:

其求解步骤如下:
1、将概率密度函数写成指数分布族的形式,得出各部分表达式;
2、从指数分布族中获取T(x)的函数形式和η的值(一般为矩阵),通常情况下取T(x)的矩阵中包含X的参数,即η1;
3、通过:
算出E(T(x))和η的关系,并将:

带入公式即可求得激活函数。
注:此为通用的一种解法,实际上当参数η只有一个时,η的反函数即为激活函数
4.1 高斯分布激活函数求解示例
通过第三节我们可以知道:

从而得到:

c代表常数,则高斯分布的激活函数可表示为:

即为线性回归。
4.2 伯努利分布激活函数求解示例
通过第三节我们可以知道:

从而得到:

c代表常数,则高斯分布的激活函数为:

即为sigmoid函数。
五、损失函数求解
对于指数分布族,我们使用极大似然估计求其通用的损失函数。从上面我们知道其表达式为:

其中:

由于训练样本之间是相互独立的,可以看成离散型随机变量,训练样本集的似然函数可以写成:

其对数似然函数为(对函数取对数,不改变原函数的极值和单调性,简化计算):

此时我们需要注意的是,η如果是一个矩阵,即多个值的时候,我们一般取与x相乘的η作为参数计算,其他视为常数,这个和计算激活函数是一样的。
其损失函数J也就是负的最大似然函数。对最大似然函数求梯度可得参考链接1、参考链接2:

从式子中我们可以发现:

所以,梯度公式为:

其海赛矩阵为:

其中:

六、模型训练方式
6.1 牛顿-拉弗迭代法

6.2 梯度下降


开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)