并行矩阵乘法(C++ mpi 并行实现)
矩阵乘法(C++ mpi 并行实现)
矩阵乘法有2种思路,我最先想到的是第一种思路,但是时间、空间复杂度都比较高。后面参考了一些资料,实现了第二种思路。
一、思路1:按行、列分块
矩阵乘法有一个很好的性质,就是结果矩阵的每个元素是不互相依赖的,因此我们可以很好地实现并行。
假如想要计算的矩阵如下:

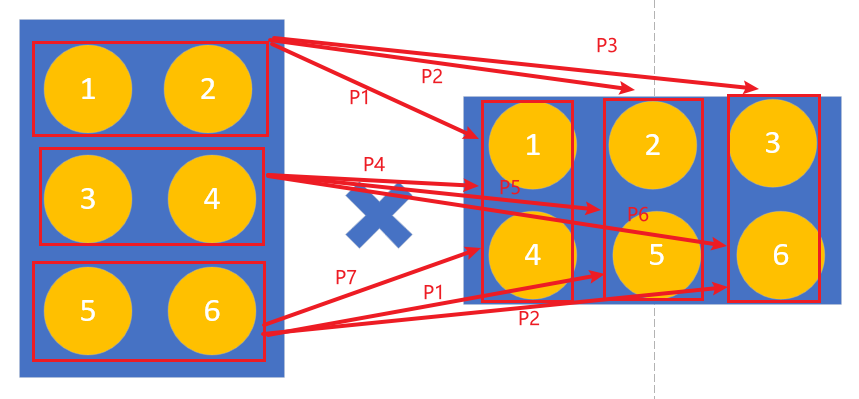
如果有8个进程,0号进程用于数据分发,其它进程用于计算,具体的分块如下图所示:

但是这种思路实现后会报错 Out of memory,具体原因后面分析。

思路1因为只传递了单行的数组,而二维vector单行数组是连续的,因此这里直接用二维vector表示矩阵就可以,代码如下:
#include <stdio.h>
#include <mpi.h>
#include<iostream>
#include<vector>
#include <cstdlib>
using namespace std;
int main(int argc, char* argv[])
{
int myrank, processNum; // myrank: 进程号; processNum: 进程总数
char processor_name[MPI_MAX_PROCESSOR_NAME];
int namelen;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &myrank);
MPI_Comm_size(MPI_COMM_WORLD, &processNum);
MPI_Get_processor_name(processor_name, &namelen); // 获取处理器名称
double startTime, endTime; // 开始时间和结束时间
// 如果是 0 号进程,随机初始化矩阵数据
int row = 3000, middleColumn = 200, column = 300; // 矩阵 A 的行数、矩阵 A 的列数和 B 的行数、矩阵 B 的行数
if (myrank == 0) { // 地主进程
vector<vector<int>> A(row, vector<int>(middleColumn));
vector<vector<int>> B(middleColumn, vector<int>(column));
// 随机初始化矩阵 A 和 B
for (int i = 0; i < row; i++) {
for (int j = 0; j < middleColumn; j++) {
A[i][j] = rand() % 10;
}
}
for (int i = 0; i < middleColumn; i++) {
for (int j = 0; j < column; j++) {
B[i][j] = rand() % 10;
}
}
// 打印矩阵 A 和 B
// cout << "A:" << endl;
// for (int i = 0; i < row; i++) {
// cout << " ";
// for (int j = 0; j < middleColumn; j++) {
// cout << A[i][j] << " ";
// }
// cout << endl;
//}
// cout << "B:" << endl;
// for (int i = 0; i < middleColumn; i++) {
// cout << " ";
// for (int j = 0; j < column; j++) {
// cout << B[i][j] << " ";
// }
// cout << endl;
// }
startTime = MPI_Wtime(); // 开始计时
int farmersProcessNum = processNum - 1; // 农民进程数
// 分发矩阵 A 和 B
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
int destProcess = (i * row + j) % farmersProcessNum + 1; // 目标进程号
MPI_Send(A[i].data(), middleColumn, MPI_INT, destProcess, 0, MPI_COMM_WORLD);
vector<int> BColumn(middleColumn);
for (int k = 0; k < middleColumn; k++) {
BColumn[k] = B[k][j];
}
MPI_Send(BColumn.data(), middleColumn, MPI_INT, destProcess, 0, MPI_COMM_WORLD);
}
}
}
else { // 农民进程 (进程号 > 0 的进程)
int count = (row * column) / (processNum - 1); // 每个进程计算的数量
int remainder = (row * column) % (processNum - 1); // 均分后多出来的待计算数
if (myrank <= remainder) {
count++;
}
for (int i = 0; i < count; i++) {
// 接收矩阵 ARow 和 BColumn
vector<int> ARow(middleColumn);
vector<int> BColumn(middleColumn);
MPI_Recv(ARow.data(), middleColumn, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
MPI_Recv(BColumn.data(), middleColumn, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
// 计算矩阵乘法
int result = 0;
for (int j = 0; j < middleColumn; j++) {
result += ARow[j] * BColumn[j];
}
// 发送计算结果
MPI_Send(&result, 1, MPI_INT, 0, 0, MPI_COMM_WORLD);
}
}
// 收集计算结果
if (myrank == 0) {
vector<vector<int>> C(row, vector<int>(column));
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
// 计算农民进程的数量
int farmersProcessNum = processNum - 1;
// 计算接收的进程号
int sourceProcess = (i * row + j) % farmersProcessNum + 1;
MPI_Recv(&C[i][j], 1, MPI_INT, sourceProcess, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
}
endTime = MPI_Wtime(); // 结束计时
// 打印矩阵 C
//cout << "C:" << endl;
//for (int i = 0; i < row; i++) {
// cout << " ";
// for (int j = 0; j < column; j++) {
// cout << C[i][j] << " ";
// }
// cout << endl;
//}
// 打印计算时间
cout << "Time: " << endTime - startTime << "s" << endl;
}
MPI_Finalize();
return 0;
}
二、思路2:矩阵分块乘法
如果我们想要计算的矩阵如下:

同时,如果我们采用4个进程来计算这个矩阵乘法,0号进程用于数据分发,其它进程用于计算,如图:

1维数组表示2维数组
思路2的算法实现,由于我们进行MPI_Send发送数组的时候,必须提供一个连续地址的数组的首地址,而思路2不同于思路1只发送1行数据,它是要发送多行的。
这就要求我们不可以使用二维数组来实现,因为二维数组不同行的首尾地址并不是连续的。具体见这篇文章:https://blog.csdn.net/weixin_44560698/article/details/120566680.
所以,这里我们使用1维数组,表示2维数组,代码如下:
#include<iostream>
#include<vector>
#include<mpi.h>
using namespace std;
// 输入:两个一维vector,表示矩阵,输出矩阵的row,middleColumn,column
// 输出:一维vector,表示两个输入vector的乘积
vector<int> matrixMultiplication(vector<int> A, vector<int> B, int row, int middleColumn, int column) {
vector<int> res(row * column);
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
int tmp = 0;
for (int k = 0; k < middleColumn; k++) {
// A[i][k] * B[k][j]
tmp += A[i * middleColumn + k] * B[k * column + j];
}
// res[i][j] = tmp
res[i * column + j] = tmp;
}
}
return res;
}
int main(int argc, char* argv[])
{
int myrank, processNum;
char processor_name[MPI_MAX_PROCESSOR_NAME];
int namelen;
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &myrank);
MPI_Comm_size(MPI_COMM_WORLD, &processNum);
MPI_Get_processor_name(processor_name, &namelen);
// 如果是 0 号进程,随机初始化矩阵数据
int row = 3000, middleColumn = 2000, column = 3000;
int farmerProcessNum = processNum - 1; // farmer 进程的数量
int chunkSize = row / farmerProcessNum; // 每个 farmer 进程处理的行数
int chunkSizeRemainder = row % farmerProcessNum; // 均分后的余数
double startTime, endTime; // 记录开始和结束时间
if (myrank == 0) { // 地主进程
vector<int> A(row * middleColumn);
vector<int> B(middleColumn * column);
// 随机初始化矩阵 A 和 B
for (int i = 0; i < row * middleColumn; i++) {
A[i] = rand() % 10;
}
for (int i = 0; i < middleColumn * column; i++) {
B[i] = rand() % 10;
}
// 打印矩阵 A 和 B
//cout << "A:" << endl;
//for (int i = 0; i < row; i++) {
// cout << " ";
// for (int j = 0; j < middleColumn; j++) {
// cout << A[i * middleColumn + j] << " ";
// }
// cout << endl;
//}
//cout << "B:" << endl;
//for (int i = 0; i < middleColumn; i++) {
// cout << " ";
// for (int j = 0; j < column; j++) {
// cout << B[i * column + j] << " ";
// }
// cout << endl;
//}
// 记录程序开始时间
startTime = MPI_Wtime();
int startRow = 0, endRow = 0; // 每个 farmer 进程处理的起始行和结束行
// 将矩阵 A 和 B 分发给其他进程
for (int i = 1; i < processNum; i++) {
// 计算下一个进程处理的结束行
endRow = startRow + chunkSize - 1;
if (i <= chunkSizeRemainder) {
endRow++;
}
int tmpRow = endRow - startRow + 1;
// 将矩阵 A 部分的数据分发给其他进程
MPI_Send(A.data() + startRow * middleColumn, tmpRow * middleColumn, MPI_INT, i, 0, MPI_COMM_WORLD);
// 将矩阵 B 所有的数据分发给其他进程
MPI_Send(B.data(), middleColumn * column, MPI_INT, i, 0, MPI_COMM_WORLD);
// 更新下一个进程处理的起始行
startRow = endRow + 1;
}
}
else { // 农民进程 (进程号 >= 1)
// 计算行数
int tmpRow = chunkSize;
if (myrank <= chunkSizeRemainder) {
tmpRow++;
}
// 计算列数
int tmpColumn = column;
// 计算中间列数
int tmpMiddleColumn = middleColumn;
// 接收矩阵 A 的数据
vector<int> A(tmpRow * tmpMiddleColumn);
MPI_Recv(A.data(), tmpRow * tmpMiddleColumn, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
// 接收矩阵 B 的数据
vector<int> B(tmpMiddleColumn * tmpColumn);
MPI_Recv(B.data(), tmpMiddleColumn * tmpColumn, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
// 计算矩阵乘法
vector<int> res = matrixMultiplication(A, B, tmpRow, tmpMiddleColumn, tmpColumn);
// 将计算结果返回给 0 号进程
MPI_Send(res.data(), tmpRow * tmpColumn, MPI_INT, 0, 0, MPI_COMM_WORLD);
}
// 0 号进程接收其他进程的计算结果
if (myrank == 0) {
vector<int> res(row * column);
int startRow = 0, endRow = 0; // 每个 farmer 进程处理的起始行和结束行
for (int i = 1; i < processNum; i++) {
// 计算下一个进程处理的结束行
endRow = startRow + chunkSize - 1;
if (i <= chunkSizeRemainder) {
endRow++;
}
int tmpRow = endRow - startRow + 1;
// 将矩阵 A 部分的数据分发给其他进程
MPI_Recv(res.data() + startRow * column, tmpRow * column, MPI_INT, i, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
// 更新下一个进程处理的起始行
startRow = endRow + 1;
}
// 记录程序结束时间
endTime = MPI_Wtime();
// 打印计算结果
//cout << "res:" << endl;
//for (int i = 0; i < row; i++) {
// cout << " ";
// for (int j = 0; j < column; j++) {
// cout << res[i * column + j] << " ";
// }
// cout << endl;
//}
// 打印计算时间
cout << "Time: " << endTime - startTime << "s" << endl;
}
MPI_Finalize();
return 0;
}
三、算法性能对比
1. 时间复杂度
思路一 300 × 200 300\times 200 300×200 和 200 × 300 200 \times 300 200×300 相乘所耗费的时间为8.83s。

相同规模的矩阵相乘,思路2的时间是0.07s。

可以看到差距还是很大的。
我们再来看一下串行程序的运行时间:

串行程序的运行时间是0.321s,看来如果我们采用思路一的并行方法就真有点得不偿失了。
这里给出我写的串行代码:
#include<iostream>
#include<vector>
using namespace std;
// 输入:两个一维vector,表示矩阵,输出矩阵的row,middleColumn,column
// 输出:一维vector,表示两个输入vector的乘积
vector<int> matrixMultiplication(vector<int> A, vector<int> B, int row, int middleColumn, int column) {
vector<int> res(row * column);
for (int i = 0; i < row; i++) {
for (int j = 0; j < column; j++) {
int tmp = 0;
for (int k = 0; k < middleColumn; k++) {
// A[i][k] * B[k][j]
tmp += A[i * middleColumn + k] * B[k * column + j];
}
// res[i][j] = tmp
res[i * column + j] = tmp;
}
}
return res;
}
int main() {
// 矩阵 A 的行数、矩阵 A 的列数和 B 的行数、矩阵 B 的行数
int row = 300, middleColumn = 200, column = 300;
vector<int> A(row * middleColumn);
vector<int> B(middleColumn * column);
// 随机初始化矩阵 A 和 B
for (int i = 0; i < row * middleColumn; i++) {
A[i] = rand() % 10;
}
for (int i = 0; i < middleColumn * column; i++) {
B[i] = rand() % 10;
}
// 记录开始和结束时间
double startTime, endTime;
startTime = clock();
vector<int> res = matrixMultiplication(A, B, row, middleColumn, column);
endTime = clock();
cout << "Time: " << (endTime - startTime) / CLOCKS_PER_SEC << "s" << endl;
// 输出 res
//for (int i = 0; i < row; i++) {
// for (int j = 0; j < column; j++) {
// cout << res[i * column + j] << " ";
// }
// cout << endl;
//}
//cout << endl;
}
我们将矩阵的大小扩大10倍,再来看:
思路1运行时间:

可以看到思路1直接out of memory了,其实是在意料之中的,具体原因可以看文章最后一部分 四、复杂度分析 。
思路2运行时间:

串行运行时间:

2. 空间复杂度
四、复杂度分析
首先,我们设:
r o w : 矩阵 A 行数 row:矩阵A行数 row:矩阵A行数
m i d d l e C o l u m n : 矩阵 A 列数和矩阵 B 行数 middleColumn:矩阵A列数和矩阵B行数 middleColumn:矩阵A列数和矩阵B行数
c o l u m n : 矩阵 B 列数 column:矩阵B列数 column:矩阵B列数
f a r m e r P r o c e s s N u m : 农民进程数 farmerProcessNum:农民进程数 farmerProcessNum:农民进程数
由于mpi主要是在并行程序之间进行通信。
对于思路1,是每次计算结果矩阵的一个元素,因此,它的总发送的数据量如下:
r o w × c o l u m n × m i d d l e C o l u m n 2 ( i n t ) row\times column \times middleColumn^2\quad (int) row×column×middleColumn2(int)
对于思路2,总发送的是A矩阵的所有+B矩阵的全部乘以进程数(因为每次都要发送B矩阵),如下:
r o w × m i d d l e C o l u m n + f a r m e r P r o c e s s N u m × m i d d l e C o l u m n × c o l u m n row\times middleColumn+farmerProcessNum\times middleColumn\times column row×middleColumn+farmerProcessNum×middleColumn×column
我们带入
r
o
w
=
3000
,
m
i
d
d
l
e
C
o
l
u
m
n
=
2000
,
c
o
l
u
m
n
=
3000
row=3000,middleColumn=2000,column=3000
row=3000,middleColumn=2000,column=3000来计算一下上述思路1需要传输的内存:
r
o
w
×
c
o
l
u
m
n
×
m
i
d
d
l
e
C
o
l
u
m
n
2
(
i
n
t
)
=
3000
×
3000
×
2000
×
2000
(
i
n
t
)
=
36
0000
0000
0000
(
i
n
t
)
=
4
×
36
0000
0000
0000
(
B
y
t
e
)
≈
131
(
T
B
)
\begin{aligned} &row\times column \times middleColumn^2\quad (int) \\ =&3000\times 3000 \times 2000\times 2000\quad (int) \\ =&36\quad 0000\quad 0000\quad 0000\quad (int) \\ =&4\times 36 \quad 0000\quad 0000\quad 0000\quad (Byte)\\ \approx&131 \quad (TB) \end{aligned}
===≈row×column×middleColumn2(int)3000×3000×2000×2000(int)36000000000000(int)4×36000000000000(Byte)131(TB)
具体转化结果如下:

传输的数据不管是传给哪个进程都是要放在内存里的,因此这种方式的空间数量级根本不可取= =。
再来看下思路2:
r o w × m i d d l e C o l u m n + f a r m e r P r o c e s s N u m × m i d d l e C o l u m n × c o l u m n ( i n t ) = 3000 × 2000 + 7 × 2000 × 3000 ( i n t ) = 4800 0000 ( i n t ) = 19200 0000 ( B y t e ) \begin{aligned} &row\times middleColumn+farmerProcessNum\times middleColumn\times column \quad (int) \\ =&3000\times 2000+7 \times 2000 \times 3000 \quad (int) \\ =&4800\quad 0000 \quad (int) \\ =&19200 \quad 0000 \quad (Byte) \end{aligned} ===row×middleColumn+farmerProcessNum×middleColumn×column(int)3000×2000+7×2000×3000(int)48000000(int)192000000(Byte)

可以看到 思路2 消耗的内存仅有 183MB ,与 思路1 的 131TB 的空间复杂度完全不在一个数量级。
结论:所以对于矩阵并行乘法,思路1是不可行的,至少也是应该是采用思路2来进行实现的。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容





所有评论(0)