Pure Pursuit 纯追踪法
介绍了几何自行车模型、纯追踪法的理论推导以及预瞄距离的确定
Pure Pursuit 纯追踪法
适用场景:低速场景(速度过高易产生转弯内切以及超调)
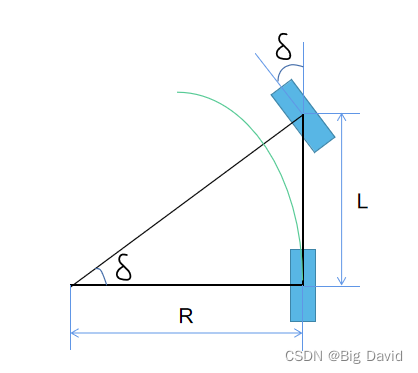
1. 几何学自行车模型

此模型在于简化前轮转向角和后轴将遵循的曲率之间的关系。
t
a
n
δ
=
L
R
\Large tan\delta =\frac{L}{R}
tanδ=RL
该公式能在较低速度的场景下对车辆运动做估计。
2. 纯追踪算法理论分析
从自行车模型出发,纯追踪算法以车后轴为切点,车辆纵向车身为切线。通过控制前轮转角,使车辆可以沿着一条经过目标路点(Gx,Gy)圆弧行驶。

(Gx,Gy)是下一个需要追踪的路点,位于已经规划好的全局路径上,现在需要控制车辆的后轴经过该路点。
- L d L_{d} Ld: 车辆后轴中心(Cx,Cy)到目标路点(Gx,Gy)的距离,即预瞄距离
- α \alpha α: 目前车身姿态和目标路点的夹角
- R R R: 跟踪的曲率半径
-
δ
δ
δ: 前轮转角
由正弦定理得:
L d s i n 2 α = R s i n ( π 2 − α ) \Large\frac{L_{d}}{sin2\alpha } =\frac{R}{sin(\frac{\pi }{2} -\alpha ){\large }} sin2αLd=sin(2π−α)R
继续往下推得 L d 2 s i n α c o s α = R c o s α \large\frac{L_{d}}{2sin\alpha cos\alpha } =\frac{R}{cos\alpha } 2sinαcosαLd=cosαR => 2 R = L d s i n α \large2R=\frac{L_{d}}{sin\alpha } 2R=sinαLd
圆弧的曲率: k a p p a = 1 R = 2 s i n α L d \large kappa =\frac{1}{R} =\frac{2sin\alpha}{Ld } kappa=R1=Ld2sinα
前轮转角 δ = a r c t a n ( L R ) = a r c t a n ( k a p p a ∗ L ) {\large \delta =arctan(\frac{L}{R} )=arctan(kappa*L){\large } } δ=arctan(RL)=arctan(kappa∗L)
纯追踪算法的最终表达式: δ ( t ) = a r c t a n ( 2 L s i n α ( t ) L d ) {\Large {\delta (t)=arctan(\frac{2Lsin\alpha (t)}{Ld} )} } δ(t)=arctan(Ld2Lsinα(t))
3. 纯追踪控制器
定义一个新的量e — 车辆当前姿态和目标路点在横向上的误差

s
i
n
α
=
e
L
d
{\large sin\alpha = \frac{e}{L_{d}}{\large }}
sinα=Lde
k a p p a = 1 R = 2 s i n α L d = 2 e L d 2 \large kappa =\frac{1}{R} =\frac{2sin\alpha}{L_{d}}=\frac{2e}{L_{d} ^2} kappa=R1=Ld2sinα=Ld22e
=>纯追踪控制器其实是一个横向误差的P控制器
K
p
=
2
L
d
2
K_{p} = \frac{2}{Ld ^2}
Kp=Ld22
这个P控制器受
L
d
L_{d}
Ld影响很大,调节预瞄距离成为纯追踪算法的关键。
4. 调节预瞄距离 L d L_{d} Ld
预瞄距离类似驾驶员开车时的视觉跟踪点。直道行驶,驾驶员会选择相对快的速度,视觉跟踪点一般也比较远;弯道行驶时,驾驶员会选择相对慢的速度,视觉跟踪点习惯选择近的位置作为跟踪参考点。
预瞄距离
L
d
L_{d}
Ld的计算与当前车辆速度v,曲率kappa存在下面的函数关系:
L d = f ( v , k a p p a ) L_{d} =f(v,kappa) Ld=f(v,kappa)
- 速度越快,预瞄距离越远,可以认为,预瞄距离与速度成正比。
- 如果前方跟踪曲率较大说明为弯道,需要减少预瞄距离满足弯道行驶的跟踪精度;曲率较小,可以增加预瞄距离保证行驶的平稳性。
所以预瞄距离 L d L_{d} Ld与速度 v v v和曲率 k a p p a kappa kappa的关系: L d ∝ v k a p p a L_{d}\propto \frac{v}{kappa} Ld∝kappav
4.1 预瞄距离 L d L_{d} Ld的确定
参考文章:基于Pure Pursuit算法的智能车路径跟踪
对于下一时刻将要跟踪的路径中,轨迹曲率K需要进行量化计算。选择一段距离内的轨迹离散化成关键点,进行评估。考虑选择合适长度的距离D内进行计算估计曲折程度。D的计算与车速成正相关。
预瞄距离
L
d
L_{d}
Ld与车速
V
V
V的数学关系:

V
V
V:车辆行驶速度
第一项: 车辆制动距离
A
=
1
2
a
m
a
x
A = \frac{1}{2a_{max}}
A=2amax1
第二项: 车辆遇到异常情况进行反应的车辆行驶距离
第三项: 车辆最小转弯半径
预瞄距离与车速的函数关系图

上述
L
d
L_{d}
Ld的计算规则,作为D的计算公式。通过计算轨迹D距离内,描述kappa。kappa的计算可以由离散路径点的曲率均值或者方差来表示。
确定预瞄距离
L
d
L_{d}
Ld后,根据Pure Pursuit算法继续计算出控制参数(
V
,
W
V,W
V,W)。
前轮转角
δ
\delta
δ对应角速度
W
W
W:
W
=
V
/
R
=
k
∗
V
W = V/R=k*V
W=V/R=k∗V
为了保证车辆在转弯时能过平稳跟踪,需要防止车辆侧翻,根据车辆自身参数对车辆运动过程中的侧向加速度进行限制。
车辆所能承受的最大侧向加速度:
A
c
c
m
a
x
=
V
m
a
x
2
R
m
i
n
Acc_{max}=\frac{V_{max}^2}{R_{min}}
Accmax=RminVmax2
当前控制参数的侧向加速度为:
A
c
c
=
W
∗
V
Acc = W*V
Acc=W∗V
如果当前控制参数的侧向加速度大于设置的阈值,那么此时的侧向加速度为阈值,并根据侧向加速度和角速度计算出此时的线速度 V V V,以保证车辆在转弯过程中的平稳性和舒适性。通常情况下, A c c m a x Acc_{max} Accmax的阈值可以设置较小一点,这样在弯道时速度较低,跟踪的精度会更好一些。
同时,为了保证控制参数平稳,Autoware还加入了低通滤波,防止控制参数突变造成车辆状态变化过快。
4.2 计算流程
纯追踪法的计算流程如下

设置固定的前视距离和路径曲率肯定无法适应不同的路径,因此就需要对于前视距离的计算方法进行研究改进。
本文详细阐述了几何自行车模型、纯追踪算法的理论推导、以及预瞄距离(有些地方叫前视距离)的确定,希望各位读者批评指正,共同学习进步。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容





所有评论(0)