卡尔曼滤波原理公式详细推导过程[包括引出]
将从最初的递归算法,利用数据融合,协方差矩阵,状态空间方程等基础推导,最终分析卡尔曼滤波5个方程全部的推导过程,其过程有很多晦涩难懂的公式,我会尽量的表达清楚和加入一些个人理解,从而使得较为便于理解
卡尔曼滤波在很多项目中都有用到,但是对于原理却很少有详细分析,而只是直接应用,在看完b站up主DR_CAN视频推导后自行推导一遍和查看其他资料后进行总结,将从最初的递归算法,利用数据融合,协方差矩阵,状态空间方程等基础推导,最终分析卡尔曼滤波5个方程全部的推导过程,其过程有很多晦涩难懂的公式,我会尽量的表达清楚和加入一些个人理解,从而使得较为便于理解,所以整个篇幅较长,大家可以在目录中寻找想查看的内容,如有其他意见,大家可以提出!
目录
一、递归算法
问题:大家在平时为了知道一个凹凸不平的苹果尺寸时,为了更加精确那便是多次测量取平均值,这时候便可以使用递归算法,通过结合估计值和测量值去更加逼近实际值。

这里可以看到主要有几个数据,一个是第k次的预测值,k-1的预测值,Kk以及第k的测量值。
当前估计值=上次估计值+系数*(当前测量值-上次估计值)
这里优点便是不需要追溯很久之前的数据,只需要知道上次的预测值和z次的测量值即可。

就像是苹果实际大小尺寸为20.1cm(实际大小) ,我估计大小为20.3cm(估计值)
用尺子量大小为19.9cm(测量大小,尺子存在测量误差),那么我根据估计的和测量的结合寻找一个比例从而最近的逼近这个实际大小。
那么我们应该怎么样去得到这个比例关系Kk从而更好的去结合呢?
我们估计苹果尺寸是20.3cm那么存在估计误差设为,每次估计都会变化,同样我们使用工具也是有误差的设为
这个是恒定的
这里我们给出定义
[为什么是这个定义后续会推导]
那么我们递归算法的步骤可以分为三步:

还是预测苹果,我们第一次预测尺寸是20.3cm,那我认为我估计误差是1cm(
),尺子固定误差在0.5cm(
),那么只需要我们不断执行上面三个公式,不断利用尺子测量Zk,并且不断更新估计误差,那我们就可以不断逼近实际尺寸。

这里我们利用一个例子:假设一个物体实际长度50,尺子测量误差为3,我人眼第一眼估计大小为40,我认为我和实际存在误差5,那么便可以多次测量(数据是随机的,只要在误差范围内即可),并且使用公式的步骤和流程来使用第k预测的结果不断逼近实际值,可以看到曲线,是收敛的,其收敛结果便是实际值。

递归算法主要是针对一个物体的某个状态,给出初始的估计值和估计误差,通过多次测量便可以使用递归算法来逼近实际状态,而并不是简单的求平均数。
二、数据融合(Data Fusion)
数据融合主要目的是通过俩个独立的不准确的状态得到一个较为准确的状态。
这里的数据融合和下列的协方差矩阵和状态方程都是为了引出卡尔曼滤波,要和上列的递归算法有个区分,递归算法是相当于是一个称去称苹果,是一个独立的事情去预测其某个状态,是可以从递归算法去引出卡尔曼滤波算法,其卡尔曼滤波可以是多个状态,较为复杂。
这里我们会用到正态分布的知识,其中方差E(X)代表均值也是数据的平分点,其方差S^2为数据波动的大小。
这里方差的定义为:
这里我们假设利用俩个称去称一个苹果的重量,这俩个称是相互独立的,他们称的数据和图形如下

那我们数据融合的目的就是使得俩个数据进行融合变成一个方差最小,数据较为集中的图形分布
这里我们用到了之前递归算法的公式:
但是之前是预测值和测量值作为俩个状态,这里我们将俩个称的数据Z1,Z2作为俩个状态
其数据融合主要使用公式:
我们要使数据最准确,那我们就需要其方差最小
Z1和Z2是相互独立的:

我们目的是求得方差最小,便是对k求导=0时候的极点k‘便是最小值所在的点。

这里可以得到k的表达式,这里推导也相当于解决了递推算法其Kk的公式,当已知Z1,Z2的方差代入并且使用 便可以进行数据融合得到一个更加准确的数据。
通过计算:


所以通过数据融合,我们能够得到一个更高更瘦,相当于样本波动小,数据更加集中的分布,使得我们的数据更加精确。
三、协方差矩阵
协方差矩阵可以将一个变量的方差或者俩变量的协方差
在一个矩阵中表现出来
能够快速的了解变量间的联动关系
这时候就有疑惑了,我们之前也没用矩阵也能解决问题阿,为什么现在要用矩阵了呢?
这时候我们就得想到矩阵的优越性,矩阵可以代替方程,可以将较多数据用一个矩阵便能表示,在面对较多数据或者复杂问题的时候班需要引入矩阵来分析和解决。
这里我们举个例子,将三位球员的身高,体重,年龄进行分析,分别设为x,y,z
| x | y | z | |
| 球员 | 身高 | 体重 | 年龄 |
| 尼尔迪 | 179 | 74 | 33 |
| 奥巴梅扬 | 187 | 80 | 31 |
| 萨拉赫 | 175 | 71 | 28 |
| 平均值 | 180.3 | 75 | 30.7 |
根据方差的定义去求,
,
,
,
,
这里协方差定义为: 其他同理分析
于是我们算出来:
、
、
、
.
这里我们定义:协方差矩阵
我们将上列算出来的方差以及协方差代入,这里还存在一个性质便是,在之后会用到
通过查看协方差矩阵可以快速的分析其变量之间的关系,例如很大说明xy的正相关性很强
这里我们需要将平均数以及变量的方差和协方差计算出来,运算量较大,这时候引入过渡矩阵,利用过渡矩阵a只需要初始数据便可以求出协方差矩阵。
假设三个变量并且三个数据:
对于协方差矩阵主要是引出p的定义及公式计算,说明在较多变量和数据时候使用协方差可以方便的看出变量之间的关系。
四、状态空间方程
这里我们利用弹簧的状态方程来分析和推导

我们写出状态方程:

1、通过公式可以由初始的x1和x2的状态变量可以得到进一步的俩个状态[计算出来的数据]
这里有了多个状态并且拥有多个系数,我们便可以使用矩阵来优化,一定要特别注意这里变量都是矩阵,而不是简单的一个数据,A、B分别代表其系数矩阵,X代表变量矩阵。
2、通过测量出来的 ,其Z1代表位置,Z2代表速度。
所以我们得到俩个公式,X(t)代表计算出来的数据,Z(t)代表测量出来的数据:

这里我们设定其数据是连续的,但是实际我们读取数据的时候并不需要那么多数据,所以我们需要将其离散化并且由于整个系统过程中,计算和测量都存在误差,我们把其认为是噪音,过程噪音Wk-1在计算过程中,测量噪音Vk在测量中,则可以得到非常重要的俩个公式。
这里需要注意的点是Xk-1和Uk-1和Wk-1,因为由上列推导,我们能够看到是由当前状态去推下一状态,所以其X和U都是上一次的数据,而测量是依据当前的数据实际记录的。
这里噪音前提是满足正态分布:
方差我们还需要利用一个知识点:Var(x)=
=
其0代表期望E(w)=0,由于w也是矩阵,并不是简单的方差表示Q,而Q表示为协方差矩阵
我们在协方差矩阵已经推导:
由于已知E(w)=0,所以=0,所以
=
所以:
假设俩个状态: 我们可以推导出Q的表达式如下:

所以我们知道了俩个公式: 、
五、 卡尔曼滤波核心公式推导
通过之前的递归算法、数据融合、协方差矩阵以及状态方程的铺垫,大家还是觉得挺复杂的吧,但是你如果把思想了解了对于后续的帮助很大,你若是将全部过程和公式推导一遍,那么你会对整个公式有很深的了解,所以不要放弃,接下来看核心公式的推导吧!
先直接给出五个核心的公式,下面便是进行部分公式的说明和推导:并不是按顺序的!
5.1 第一个公式(预测)
在状态空间方程那部分我们已经推导了:
卡尔曼滤波就是将测量数据和预测数据进行融合得到一个更加精确的数据, 这里我们首先分析理想的状态,即没有带入噪音,并将其计算值改为估计值,没有加入噪声的估计值为先验估计值。
这里第一个数值便是估计值,第二个Zk便是测量值,但是需要注意的是若有多个状态其中变量表示的是矩阵而不是简单的一个数据。
5.2 第四个公式(后验估计)
我们已经得到俩个数据,先验估计数据和测量数据,那么我们利用数据融合思想
当G=0的时候,=
完全信任估计值,当G=1时候
=
完全相信测量值
为了解决H不可逆的问题,将其替换并出现最重要的kalman gain
得到公式:
这时候,当Kk=0的时候=
,信任估计值,当Kk=
时,
=
5.3 第三个公式 (卡尔曼增益)
在5.2我们通过后验估计结合数据融合将其公式写出来了,但是这时候便是寻找一个Kk使得估计值最逼近实际值Xk,结合数据融合,便是求得
方差最小,结合协方差矩阵,方差
最小
由于估计值和实际值一定有个误差:
这里定义俩个状态,则方差便是迹tr(P)=
最小。


所以我们得到了kalman gain的表达式,并且在这里R是测量噪声,当R很大的时候,Kk=0,表示完全信任估计值,当R=0,则=
完全信任测量值。
5.4 第2个公式 (先验误差协方差)
这里我们得到了三个公式,但是我们在Kk中存在一个未知的
,即先验误差协方差,只有知道这个Kk才能知道。

我们已经得到了的表达式,但是
每次都会变化于是需要不断更新,并引出了第五个公式
5.5 第5个公式(更新误差协方差)
在推导Kk的时候有公式:
所以5个公式已经全部推导完毕了,最好给出这5个公式之间的联系:

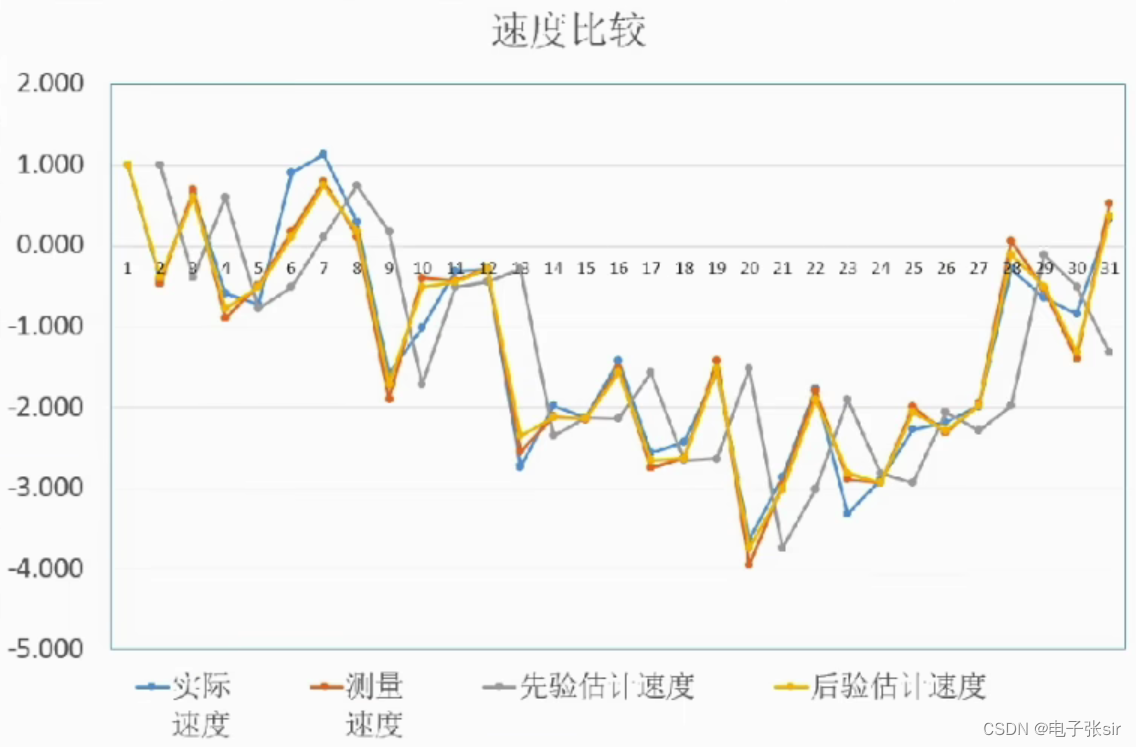
可以利用二维的例子去更加熟悉卡尔曼滤波的过程的结果,通过分析其图形从而更好的了解原理
EXCEL程序下载链接:https://pan.baidu.com/s/1GdJe2eWIlaQrk2nrjemRCQ
提取码:txn3
密码:6.66


要看详细这个实例的分析可以看这篇博文也讲了: http://t.csdn.cn/oAI5E
以下是手动推导过程,在piad上记录了但是没有这种大界面清晰,有时间也是建议大家可以推推



好了整个过程就结束了,整个篇幅较长,若是搞懂需要较长的时间去仔细的推导和演算,希望对大家有帮助,有问题需要改进的地方也欢迎大家提出!
参考资料:
B站up主:DR_CAN: 【卡尔曼滤波器】_Kalman Filter_全网最详细数学推导

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容






所有评论(0)