(十六) 基于cadence 617 手算参数 μnCox,λ ,VTH仿真
大多数人都知道——即使是大量随机排列字符的猴子也写不出一本有趣的书,一些人往往会忘记的是——即使是大量的 ”Spice Monkeys” 随机调整电路也永远无法设计出稳健、优化的电路,简单地说 Spice 只是一个 “计算器”,让你评估和测试你的想法,去验证你设计的电路。现在通过仿真 MOS 管的 I-V 曲线去估算工艺参数,以方便在以后的电路设计中提供估算参数。
一、前言
大多数人都知道——即使是大量随机排列字符的猴子也写不出一本有趣的书,一些人往往会忘记的是——即使是大量的 ”Spice Monkeys” 随机调整电路也永远无法设计出稳健、优化的电路, 简单地说 Spice 只是一个 “计算器” ,让你评估和测试你的想法,去验证你设计的电路。现在通过仿真 MOS 管的 I-V 曲线去估算工艺参数,以方便在以后的电路设计中提供估算参数。
二、I-V曲线扫描
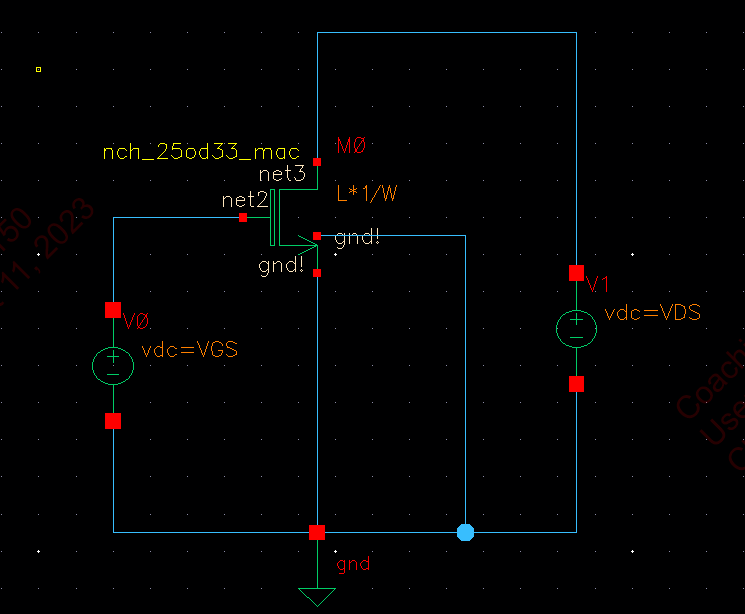
NMOS
1. 电路图
2. ADE


3. 参数扫描

4. 仿真结果

PMOS
1. 电路图

2. ADE

3. 仿真扫描
4. 仿真结果

三、I-V 参数表
NMOS
| VGS = 1V | VGS = 1.2V | |
|---|---|---|
| VDS = 0.8V | 7.096 u | 15.984 u |
| VDS = 1.5V | 7.174 u | 16.138 u |
PMOS
| VSG = 1 V | VSG = 1.2 V | |
|---|---|---|
| VSD = 0.8V | 9.91 u | 19.591 u |
| VSD = 1.5V | 10.218 u | 20.248 u |
四、 参数计算
饱和区电流公式
I
D
=
1
2
μ
n
C
o
x
W
L
(
V
G
S
−
V
T
H
)
2
(
1
+
λ
V
D
S
)
I_{D}=\frac{1}{2} \mu_{n} C_{o x} \frac{W}{L}\left(V_{G S}-V_{T H}\right)^{2}(1+\lambda V_{DS})
ID=21μnCoxLW(VGS−VTH)2(1+λVDS)
Step1
VGS = 1V ,V DS 分别为0.8 V,1.5 V(也就是 VGS = 1V 一列 ) 带入电流方程
7.096
u
=
1
2
μ
n
C
o
x
W
L
(
1
−
V
T
H
)
2
(
1
+
λ
0.8
)
(
1
)
7.174
u
=
1
2
μ
n
C
o
x
W
L
(
1
−
V
T
H
)
2
(
1
+
λ
1.5
)
7.096u=\frac{1}{2} \mu_{n} C_{o x} \frac{W}{L}\left(1-V_{T H}\right)^{2}(1+\lambda 0.8)\\ (1)\\ 7.174u=\frac{1}{2} \mu_{n} C_{o x} \frac{W}{L}\left(1-V_{T H}\right)^{2}(1+\lambda 1.5)\\
7.096u=21μnCoxLW(1−VTH)2(1+λ0.8)(1)7.174u=21μnCoxLW(1−VTH)2(1+λ1.5)
上式中的左除以左,右除以右可以得 λn = 0.016 V-1
从曲线就可以看见其斜率很小 ,λn 与 L 是成反比的关系,第一次仿真 L = 1u ,λn很小,减小 L 值后λn大了只是一点点,可能是工艺的区别吧
Step2
当V DS = 0.8V ,V GS 分别为1 V,1.2 V(也就是 VDS = 0.8V 一行 ) 带入电流方程
7.096 u = 1 2 μ n C o x W L ( 1 V − V T H ) 2 ( 1 + λ 0.8 ) 15.984 u = 1 2 μ n C o x W L ( 1.2 V − V T H ) 2 ( 1 + λ 0.8 ) 7.096 u=\frac{1}{2} \mu_{n} C_{o x} \frac{W}{L}\left(1V-V_{T H}\right)^{2}(1+\lambda 0.8)\\ 15.984u=\frac{1}{2} \mu_{n} C_{o x} \frac{W}{L}\left(1.2V-V_{T H}\right)^{2}(1+\lambda 0.8) 7.096u=21μnCoxLW(1V−VTH)2(1+λ0.8)15.984u=21μnCoxLW(1.2V−VTH)2(1+λ0.8)
上式左边除以左边,右除以右可以得 VTH = 0.6 V
Step3
将λn = 0.016 V-1,VTH = 0.6 V ,W = 1u,L = 550n带入 step1 中方程可以得到 Kn = μn Cox = 4.82 × 10-5 A/V2
同理可以求得
|λp| = 0.046 V-1 ,|VTH|= 0.507 V , |Kp| = μp Cox = 4.31 × 10-5 A/V2
从实际电路查看直流工作点,发现误差还是很大的,VTH 相差了63mv

五、beff 与 betaeff

b
e
f
f
=
μ
n
C
o
x
W
L
I
D
=
1
2
b
e
f
f
W
L
(
V
G
S
−
V
T
H
)
2
beff = \mu_{n} C_{o x} \frac{W}{L}\\ I_{D}=\frac{1}{2} beff \frac{W}{L}\left(V_{G S}-V_{T H}\right)^{2}
beff=μnCoxLWID=21beffLW(VGS−VTH)2
用仿真得到 VTH,电流ID ,加上beff 可以满足平方率关系式
bataeff 是考虑更多效应的结果,拉扎维书本Level 3 Model中描述
μ
1
=
μ
e
f
f
1
+
μ
e
f
f
V
D
S
v
max
L
1
μ
e
f
f
=
μ
0
1
+
θ
(
V
G
S
−
V
T
H
)
\begin{array}{l}\mu_{1}=\frac{\mu_{e f f}}{1+\frac{\mu_{e f f} V_{D S}}{v_{\max } L_{1}}}\\\mu_{e f f}=\frac{\mu_{0}}{1+\theta\left(V_{G S}-V_{T H}\right)}\end{array}
μ1=1+vmaxL1μeffVDSμeffμeff=1+θ(VGS−VTH)μ0
五、参考博客
https://blog.csdn.net/weixin_44115643/article/details/119062516
https://blog.csdn.net/qq_46579389/article/details/121505516

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容





所有评论(0)