DQN算法概述及基于Pytorch的DQN迷宫实战代码

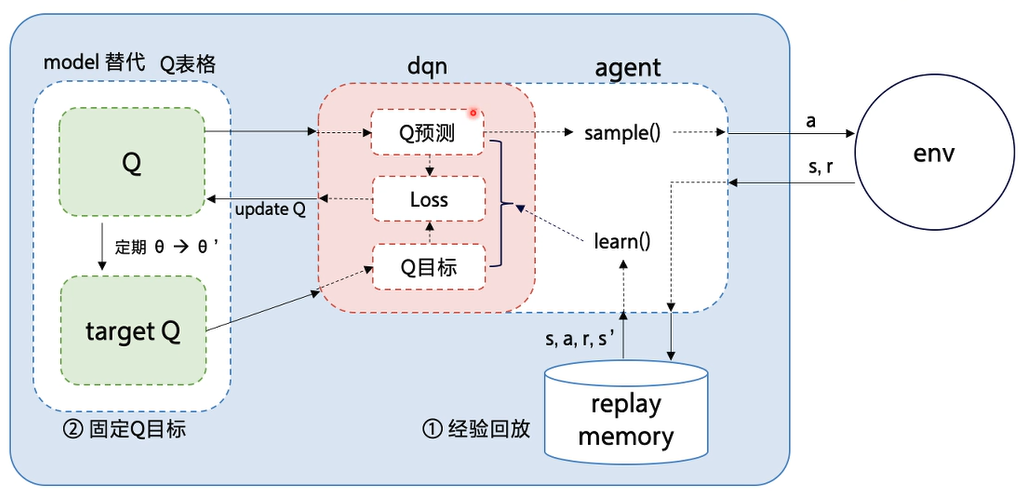
深度Q网络将Q学习与深度学习结合，用深度网络来近似动作价值函数，而Q学习则是采用表格存储；深度Q网络采用经验回放的训练方式，从历史数据中随机采样，而Q学习直接采用下一个状态的数据进行学习。

毒爪的小新

4010人浏览 · 2023-09-07 20:51:32

毒爪的小新 · 2023-09-07 20:51:32 发布

一. DQN算法概述

1.1 算法定义

Q-Learing是在一个表格中存储动作对应的奖励值，即状态-价值函数Q(s,a)，这种算法存在很大的局限性。在现实中很多情况下，强化学习任务所面临的状态空间是连续的，存在无穷多个状态，这种情况就不能再使用表格的方式存储价值函数。

于是，诞生了DQN算法，即深度Q网络（Deep Q-Network），是指基于深度学习的Q-Learing算法，用来解决连续状态空间和离散动作空间问题。此时的状态-价值函数变为Q(s,a;w)，w是神经网络训练的参数矩阵。

DQN算法有两个非常大的优点，分别是经验回放和双Q表，下面详细讲解。

1.2 经验回放

不使用经验回放DQN算法的缺点：

使用完 $s_t,a_t,r_t,s_{t+1})$ 就丢弃，造成经验浪费
我们按顺序使用四元组，前后两个transition四元组相关性很强，这种相关性对学习Q网络是有害的。

经验回放原理

经验回放会构建一个回放缓冲区（replay buffer），存储若干条transition，称为经验区，某一个策略与环境交互，收集很多条transition，放入回放缓冲区，回放缓冲区中的经验transition可能来自不同的策略。回放缓冲区只有在它装满的时候才会把旧的数据丢掉

使用经验回放优点：

能够重复使用经验，数据利用率高，对于数据获取困难的情况尤其有用。
把序列打散，消除相关性，使得数据满足独立同分布，从而减小参数更新的方差，提高收敛速度。

1.3 目标网络

不使用目标网络DQN算法的缺点

因为要计算目标网络的目标值target，会使用最大值，这样就会造成计算的结果比真实值要大，用高估的结果再去更新自己，在网络中一次次循环过程，该最大化会越来越大，导致高估。

目标网络原理

使用第二个网络，称为目标网络： $Q(s,a;{w^-})$ ，网络结构和原来的网络 $Q(s,a;{w})$ 一样，只是参数不同 ${w^-}≠w$ ，原来的网络称为评估网络

两个网络的作用不一样：

评估网络 $Q(s,a;{w})$ 负责控制智能体，收集经验，梯度下降、反向传播
目标网络 $Q(s^{\prime},a^{\prime};w^{-})$ 用于计算下一状态Q值
在更新过程中，只更新评估网络 $Q(s,a;{w})$ 的权重 $w$ ，目标网络 $Q(s,a;{w^-})$ 的权重保持 ${w^-}$ 不变，在更新一定次数后，再将更新过的评估网络的权重复制给目标网络，进行下一批更新，这样目标网络也能得到更新

使用目标网络的优点

利用目标网络可以一定程度避免自举，减缓高估问题；由于在目标网络没有变化的一段时间内回报的目标值是相对固定的，因此目标网络的引入增加了学习的稳定性。

1.4 完整训练过程

在这里插入图片描述

初始化：初始化深度神经网络 $Q$ 和目标网络 $Q_{\text{target}}$ 的权重 $\theta$ 和 $\theta^-$ 。
数据收集： 在环境中与智能体进行交互，执行动作并观察状态转移、奖励和终止状态，将这些经验存储在经验回放缓冲区中。
经验回放： 从经验回放缓冲区中随机抽样一批经验，用于更新神经网络。这有助于减少样本之间的相关性，提高训练的稳定性。
Q值估计： 使用神经网络 $Q$ 估计当前状态下所有动作的 Q 值。
目标计算： 使用目标网络 $Q_{\text{target}}$ 估计下一状态的最大 Q 值，即 $\max_{a'} Q_{\text{target}}(s', a'; \theta^-)$ 。
更新目标： 使用当前奖励和计算的目标 Q 值更新目标值：

$\mathrm{target}=r+\gamma\cdot\max_{a^{\prime}}Q_{\mathrm{target}}(s^{\prime},a^{\prime};\theta^{-})$

计算损失： 使用均方误差损失计算 Q 值估计与目标之间的差异：

$\mathcal{L}(\theta)=\frac12\left(\text{target}-Q(s,a;\theta)\right)^2$

更新网络： 使用梯度下降更新神经网络的权重 $\theta$ ，最小化损失 $\mathcal{L}(\theta)$ 。

$\nabla_\theta\mathcal{L}(\theta)=-\left(\mathrm{target}-Q(s,a;\theta)\right)\cdot\nabla_\theta Q(s,a;\theta)$

$\theta\leftarrow\theta-\alpha\cdot\nabla_\theta\mathcal{L}(\theta)$

周期性更新目标网络： 每隔一定的时间步骤，将目标网络的权重 $\theta^-$ 更新为当前网络的权重 $\theta$ 。
重复步骤2至9： 迭代地进行数据收集、经验回放、更新网络等步骤。

1.5 总结

深度Q网络将Q学习与深度学习结合，用深度网络来近似动作价值函数，而Q学习则是采用表格存储；深度Q网络采用经验回放的训练方式，从历史数据中随机采样，而Q学习直接采用下一个状态的数据进行学习。

二. 基于Pytorch的DQN迷宫实战

直接上GitHub代码吧，注释全部写在里面了，非常详细：

基于Pytorch的DQN迷宫算法

为了防止有小伙伴打不开，还是这里也放一份吧
RL.py：定义DQN网络

'''
@Author ：YZX
@Date ：2023/8/7 10:21
@Python-Version ：3.8
'''

import torch
# 用于构建神经网络的各种工具和类
import torch.nn as nn
import numpy as np
# 用于执行神经网络中的各种操作，如激活函数、池化、归一化等
import torch.nn.functional as F
import matplotlib.pyplot as plt
 
# 深度网络，全连接层
class Net(nn.Module):
    # 输入状态和动作，当前例子中状态有2个表示为坐标(x,y)，动作有4个表示为(上下左右)
    def __init__(self, n_states, n_actions):
        super(Net, self).__init__()
        # 创建一个线性层，2行10列
        self.fc1 = nn.Linear(n_states, 10)
        # 创建一个线性层，10行4列
        self.fc2 = nn.Linear(10, n_actions)
        # 随机初始化生成权重，范围是0-0.1
        self.fc1.weight.data.normal_(0, 0.1)
        self.fc2.weight.data.normal_(0, 0.1)
 
    # 前向传播（用于状态预测动作的值）
    def forward(self, state):
        # 这里以一个动作为作为观测值进行输入(输入张量)
        # 线性变化后输出给10个神经元，格式：(x,x,x,x,x,x,x,x,x,x,x)
        state = self.fc1(state)
        # 激活函数，将负值设置为零，保持正值不变
        state = F.relu(state)
        # 经过10个神经元运算过后的数据，线性变化后把每个动作的价值作为输出。
        out = self.fc2(state)
        return out
 
# 定义DQN网络class
class DQN:
    #   n_states 状态空间个数；n_actions 动作空间大小
    def __init__(self, n_states, n_actions):
        print("<DQN init> n_states=", n_states, "n_actions=", n_actions)
        # 建立一个评估网络（即eval表示原来的网络） 和 Q现实网络 （即target表示用来计算Q值的网络）
        # DQN有两个net:target net和eval net,具有选动作、存储经验、学习三个基本功能
        self.eval_net, self.target_net = Net(n_states, n_actions), Net(n_states, n_actions)
        # 损失均方误差损失函数
        self.loss = nn.MSELoss()
        # 优化器，用于优化评估神经网络更新模型参数（仅优化eval），使损失函数尽量减小
        self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=0.01)
        self.n_actions = n_actions  #   状态空间个数
        self.n_states = n_states    #   动作空间大小
 
        # 使用变量
        # 用来记录学习到第几步了
        self.learn_step_counter = 0
        # 用来记录当前指到数据库的第几个数据了
        self.memory_counter = 0
        # 创建一个2000行6列的矩阵，即表示可存储2000行经验，每一行6个特征值
        # 2*2表示当前状态state(x,y)和下一个状态next_state(x,y) + 1表示选择一个动作 + 1表示一个奖励值
        self.memory = np.zeros((2000, 2 * 2 + 1 + 1))
        self.cost = []  # 记录损失值
        self.steps_of_each_episode = []  # 记录每轮走的步数
 
    # 进行选择动作
    # state = [-0.5 -0.5]
    def choose_action(self, state, epsilon):
        # 扩展一行,因为网络是多维矩阵,输入是至少两维
        # torch.FloatTensor(x)先将x转化为浮点数张量
        # torch.unsqueeze(input, dim)再将一维的张量转化为二维的,dim=0时数据为行方向扩，dim=1时为列方向扩
        # 例如 [1.0, 2.0, 3.0] -> [[1.0, 2.0, 3.0]]
        state = torch.unsqueeze(torch.FloatTensor(state), 0)
        # 在大部分情况，我们选择 去max-value
        if np.random.uniform() < epsilon:   # greedy # 随机结果是否大于EPSILON（0.9）
            # 获取动作对应的价值
            action_value = self.eval_net.forward(state)
            #   torch.max() 返回输入张量所有元素的最大值，torch.max(input, dim)，dim是max函数索引的维度0/1，0是每列的最大值，1是每行的最大值
            #   torch.max(a, 1)[1] 代表a中每行最大值的索引
            #   data.numpy()[0] 将Variable转换成tensor
            # 哪个神经元值最大，则代表下一个动作
            action = torch.max(action_value, 1)[1].data.numpy()[0]
        # 在少部分情况，我们选择 随机选择 （变异）
        else:
            #   random.randint(参数1，参数2)函数用于生成参数1和参数2之间的任意整数，参数1 <= n < 参数2
            action = np.random.randint(0, self.n_actions)
        return action


    # 存储经验
    # 存储【本次状态，执行的动作，获得的奖励分，完成动作后产生的下一个状态】
    def store_transition(self, state, action, reward, next_state):
        # 把所有的记忆捆在一起，以 np 类型
        # 把 三个矩阵 s ,[a,r] ,s_  平铺在一行 [a,r] 是因为 他们都是 int 没有 [] 就无法平铺 ，并不代表把他们捆在一起了
        #  np.hstack()是把矩阵按水平方向堆叠数组构成一个新的数组
        transition = np.hstack((state, [action, reward], next_state))
        # index 是 这一次录入的数据在 MEMORY_CAPACITY 的哪一个位置
        # 如果记忆超过上线，我们重新索引。即覆盖老的记忆。
        index = self.memory_counter % 200
        self.memory[index, :] = transition  # 将transition添加为memory的一行
        self.memory_counter += 1


    # 从存储学习数据
    # target_net是达到次数后更新， eval_net是每次learn就进行更新
    def learn(self):
        # 更新 target_net，每循环100次更新一次
        if self.learn_step_counter % 100 == 0:
            # 将评估网络的参数状态复制到目标网络中
            # 即将target_net网络变成eval_net网络，实现模型参数的软更新
            self.target_net.load_state_dict((self.eval_net.state_dict()))
        self.learn_step_counter += 1

        # eval_net是 每次 learn 就进行更新
        # 从[0,200)中随机抽取16个数据并组成一维数组，该数组表示记忆索引值
        sample_index = np.random.choice(200, 16)
        # 表示从 self.memory 中选择索引为 sample_index 的行，: 表示选取所有列
        # 按照随机获得的索引值获取对应的记忆数据
        memory = self.memory[sample_index, :]
        # 从记忆当中获取[0,2)列，即第零列和第一列，表示状态特征
        state = torch.FloatTensor(memory[:, :2])
        # 从记忆中获取[2,3)列，即第二列，表示动作特征
        action = torch.LongTensor(memory[:, 2:3])
        # 从记忆中获取[3,4)列，即第三列，表示奖励特征
        reward = torch.LongTensor(memory[:, 3:4])
        # 从记忆中获取[4,5)列，即第四列和第五列，表示下一个状态特征
        next_state = torch.FloatTensor(memory[:, 4:6])

        # 从原来的网络中获得当前状态的动作对应的预测Q值
        # self.eval_net(state)表示输入当前state，通过forward()函数输出状态对应的Q值估计
        # .gather(1, action)表示从上述Q值估计的集合中，第一个维度上获取action对应的的Q值
        # 将Q值赋值给q_eval，表示所采取动作的预测value
        q_eval = self.eval_net(state).gather(1, action)

        # 获得下一步状态的Q值
        # 把target网络中下一步的状态对应的价值赋值给q_next；此处有时会反向传播更新target，但此处不需更新，故加.detach()
        q_next = self.target_net(next_state).detach()

        # 计算对于的最大价值
        # q_target 实际价值的计算  ==  当前价值 + GAMMA（未来价值递减参数） * 未来的价值
        # max函数返回索引的最大值
        # unsqueeze(1)将上述计算出来的最大 Q 值的张量在第 1 个维度上扩展一个维度，变为一个列向量。
        q_target = reward + 0.9 * q_next.max(1)[0].unsqueeze(1)

        # 通过预测值与真实值计算损失 q_eval预测值， q_target真实值
        loss = self.loss(q_eval, q_target)
        # 记录损失值
        self.cost.append(loss.detach().numpy())
        # 根据误差，去优化我们eval网, 因为这是eval的优化器
        # 反向传递误差，进行参数更新
        self.optimizer.zero_grad()  # 梯度重置
        loss.backward()  # 反向求导
        self.optimizer.step()  # 更新模型参数

    # 绘制损失图
    def plot_cost(self):
        # np.arange(3)产生0-2数组
        plt.plot(np.arange(len(self.cost)), self.cost)
        plt.xlabel("step")
        plt.ylabel("cost")
        plt.show()

    # 绘制每轮需要走几步
    def plot_steps_of_each_episode(self):
        plt.plot(np.arange(len(self.steps_of_each_episode)), self.steps_of_each_episode)
        plt.xlabel("episode")
        plt.ylabel("done steps")
        plt.show()

MazeEnv.py：创建环境地图

'''
@Author ：YZX
@Date ：2023/8/7 16:03
@Python-Version ：3.8
'''

import tkinter as tk
import numpy as np
 
UNIT = 40  # pixels 像素
MAZE_H = 4  # grid height y轴格子数
MAZE_W = 4  # grid width x格子数
 
# 迷宫
class Maze(tk.Tk, object):
    def __init__(self):
        print("<env init>")
        super(Maze, self).__init__()
 
        # 动作空间(定义智能体可选的行为),action=0-3
        self.action_space = ['u', 'd', 'l', 'r']
        # 使用变量
        self.n_actions = len(self.action_space)
        # 状态空间，state=0,1
        self.n_states = 2
 
        # 配置信息
        self.title('maze')
        # 设置屏幕大小
        self.geometry("160x160")
 
        # 初始化操作
        self.__build_maze()
 
    # 渲染画面
    def render(self):
        # time.sleep(0.1)
        self.update()
 
    # 重置环境
    def reset(self):
        # 智能体回到初始位置
        # time.sleep(0.1)
        self.update()
        self.canvas.delete(self.rect)
 
 
        origin = np.array([20, 20])
 
        # 智能体位置，前两个左上角坐标(x0,y0)，后两个右下角坐标(x1,y1)
        self.rect = self.canvas.create_rectangle(
            origin[0] - 15, origin[1] - 15,
            origin[0] + 15, origin[1] + 15,
            fill='red')
 
        # return observation 状态
        # canvas.coords(长方形/椭圆),会得到 【左极值点、上极值点、右极值点、下极值点】这四个点组成的元组，:2表示前2个
        return (np.array(self.canvas.coords(self.rect)[:2]) - np.array(self.canvas.coords(self.oval)[:2])) / (MAZE_H * UNIT)
 
 
    # 智能体向前移动一步：返回next_state,reward,terminal
    def step(self, action):
        s = self.canvas.coords(self.rect)
        base_action = np.array([0, 0])
        if action == 0:  # up
            if s[1] > UNIT:
                base_action[1] -= UNIT
        elif action == 1:  # down
            if s[1] < (MAZE_H - 1) * UNIT:
                base_action[1] += UNIT
        elif action == 2:  # right
            if s[0] < (MAZE_W - 1) * UNIT:
                base_action[0] += UNIT
        elif action == 3:  # left
            if s[0] > UNIT:
                base_action[0] -= UNIT
 
        self.canvas.move(self.rect, base_action[0], base_action[1])  # move agent
 
        next_coords = self.canvas.coords(self.rect)  # next state
 
        # reward function
        if next_coords == self.canvas.coords(self.oval):
            reward = 1
            print("victory")
            done = True
        elif next_coords in [self.canvas.coords(self.hell1)]:
            reward = -1
            print("defeat")
            done = True
        else:
            reward = 0
            done = False
        s_ = (np.array(next_coords[:2]) - np.array(self.canvas.coords(self.oval)[:2])) / (MAZE_H * UNIT)
        return s_, reward, done
 
    def __build_maze(self):
        self.canvas = tk.Canvas(self, bg='white',
                                height=MAZE_H * UNIT,
                                width=MAZE_W * UNIT)
 
        # create grids
        for c in range(0, MAZE_W * UNIT, UNIT):
            x0, y0, x1, y1 = c, 0, c, MAZE_H * UNIT
            self.canvas.create_line(x0, y0, x1, y1)
        for r in range(0, MAZE_H * UNIT, UNIT):
            x0, y0, x1, y1 = 0, r, MAZE_W * UNIT, r
            self.canvas.create_line(x0, y0, x1, y1)
        origin = np.array([20, 20])
        hell1_center = origin + np.array([UNIT * 2, UNIT])
        # 陷阱
        self.hell1 = self.canvas.create_rectangle(
            hell1_center[0] - 15, hell1_center[1] - 15,
            hell1_center[0] + 15, hell1_center[1] + 15,
            fill='black')
        oval_center = origin + UNIT * 2
        # 出口
        self.oval = self.canvas.create_oval(
            oval_center[0] - 15, oval_center[1] - 15,
            oval_center[0] + 15, oval_center[1] + 15,
            fill='yellow')
        # 智能体
        self.rect = self.canvas.create_rectangle(
            origin[0] - 15, origin[1] - 15,
            origin[0] + 15, origin[1] + 15,
            fill='red')
        self.canvas.pack()

Run.py：训练主方法

'''
@Author ：YZX
@Date ：2023/8/7 16:03
@Python-Version ：3.8
'''

from MazeEnv import Maze
from RL import DQN
import time

 
def run_maze():
    print("====Game Start====")
 
    step = 0    # 已进行多少步
    max_episode = 500   # 总共需要进行多少轮
 
    for episode in range(max_episode):

        # 环境和位置重置，但是memory一直保留
        state = env.reset()

        # 本轮已进行多少步
        step_every_episode = 0
        # 动态变化随机值
        epsilon = episode / max_episode
 
        # 开始实验循环
        # 只有env认为 这个实验死了，才会结束循环
        while True:
            if episode < 10:
                time.sleep(0.1)
            if episode > 480:
                time.sleep(0.2)
 
            # 刷新环境状态，显示新位置
            env.render()
            # 根据输入的环境特征 s  输出选择动作 a
            action = model.choose_action(state, epsilon)  # 根据状态选择行为
            # 环境根据行为给出下一个状态，奖励，是否结束。
            next_state, reward, terminal = env.step(action) # env.step(a) 是执行 a 动作
            # 每完成一个动作，记忆存储数据一次
            model.store_transition(state, action, reward, next_state)  # 模型存储经历

            # 按批更新
            if step > 200 and step % 5 == 0:
                model.learn()
 
            # 状态转变
            state = next_state

            # 状态是否为终止
            if terminal:
                print("episode=", episode, end=",") # 第几轮
                print("step=", step_every_episode)  # 第几步
                model.steps_of_each_episode.append(step_every_episode) # 记录每轮走的步数
                break
 
            step += 1   # 总步数+1
            step_every_episode += 1 # 当前轮的步数+1
 
    # 游戏环境结束
    print("====Game Over====")
    env.destroy()
 
 
if __name__ == "__main__":
    env = Maze()  # 环境
    # 实例化DQN类，也就是实例化这个强化学习网络
    model = DQN(n_states=env.n_states,n_actions=env.n_actions)
    run_maze()  # 训练
 
    env.mainloop()  # mainloop()方法允许程序循环执行,并进入等待和处理事件
    model.plot_cost()  # 画误差曲线
    model.plot_steps_of_each_episode()  # 画每轮走的步数