呼吸与心跳是人体重要的生理过程，在一定程度上能够反映人体的身体状况，因此呼吸和心跳的检测在临床诊断、疾病预防上显得尤为重要。目前，呼吸和心跳的检测包括以下两大类：接触式的和非接触式的。对于接触式方法，设备比较成熟，但使用受局限，烧伤病人无法使用，普通人使用比较麻烦。而对于非接触方法，设备使用比较灵活，其中雷达式生命检测仪具有穿透能力强的优点。在一些非常规的应用场景（如烧伤、传染等）下它能够完成生命体征数据的采集与检测，适合养老院等单位对老人睡眠状况的检测，但存在呼吸和心跳信号难以分离的技术难题。下面简单介绍本科时期本人针对这个问题所作的一些研究。

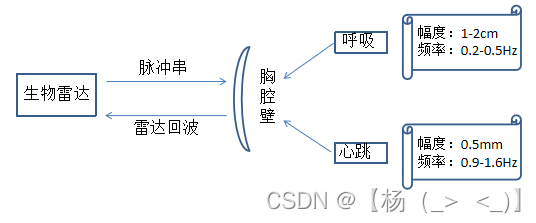
一、检测原理

上图为检测原理图，可以分两步理解：一方面呼吸和心跳会引起人体胸腔壁的起伏运动，起伏的频率包含呼吸和心跳的频率信息；另一方面，雷达具有测距功能可以测出物体运动信息。这样通过雷达探测胸腔壁，我们可以获得包含呼吸和心跳频率信息的雷达回波信号，通过信号处理手段分析雷达回波信号进而得到呼吸心跳信息便是本研究的最终目标。

二、信号模型

为了设计与实际场景相匹配的信号处理方法，一个关键的工作是对场景进行信号建模，信号建模的重要性以及困难之处在于：一方面所建信号模型应尽量符合实际场景（准确）；另一方面所建信号模型应尽量简单（简洁），便于设计简单高效的信号处理方法。

考虑到本研究最终是要估计出呼吸与心跳的频率信息，所以综合考虑模型准确性和简洁性，我们假设呼吸与心跳引起的胸腔壁运动符合简单的余弦函数关系，函数频率为呼吸与心跳所对应的频率，由此得到雷达与胸腔壁的距离为：

$R\left ( t \right )=R_{0}+A_{b}\sin\left ( 2\pi f_{b} t+\varphi _{b}\right )+A_{h}\sin\left ( 2\pi f_{h}t +\varphi _{h}\right )$

其中 $R_{0}$ 为人的位置距离， $A_{b}$ ， $f_{b}$ ， $\varphi _{b}$ 分别为呼吸引起胸腔壁运动的幅度、频率以及相位。 $A_{h}$ ， $f_{h}$ ， $\varphi _{h}$ 分别为心跳引起胸腔壁运动的幅度、频率以及相位。

由此，下变频后的基带回波信号为：

$r\left ( t \right )=e^{-j\frac{4\pi}{\lambda }R\left ( t \right )}$

三、检测估计方法

3.1 直接对回波信号分析

考虑到相位为余弦函数的信号可以分解如下：

$e^{a\sin \left ( 2\pi ft \right )}=\sum J_{k}\left ( a \right )e^{j2\pi kft}$

其中， $J_{k}\left ( x \right )$ 为第一类bessel函数。由此可以判断出回波信号的频率成分由呼吸频率和心跳频率及其谐波组合而成。

上图是假设心跳1Hz，幅度0.5mm，呼吸0.3Hz，幅度15mm下回波信号的频谱图，可以看出呼吸信号的高次谐波分量的旁瓣将心跳信号主分量淹没，导致心跳信号难以检测到。为此，文章考虑利用回波信号的相位信息还原胸腔壁的运动信息，通过分析胸腔壁的运动信息得到呼吸心跳信号的频率信息。

3.2 回波信号相位分析

通过信号建模可以发现回波基带信号的相位反映了胸腔壁的运动信息，由此可以通过分析回波信号的相位信息得到胸腔壁的运动信息，进而得到呼吸心跳的频率信息。

上图是假设心跳1.1Hz，幅度0.25mm，呼吸0.17Hz，幅度6mm下由回波信号相位信息还原的运动信息与雷达胸腔壁瞬时距离的对比，可以看出回波信号的相位还原的运动信息能够反映呼吸心跳特征，可以由此估计其对应的频率信息，下图是对应的运动信号曲线的频谱，可以频谱可以很容易得到呼吸与心跳的频率信息。这样也就确定了文章针对呼吸心跳检测方法的基本原理。之后剩下的信号处理部分是针对含噪情况下进行的。

四、实验验证

由于超宽带雷达发射功率较低，对人体影响小；所需功耗小，系统供电方便，产品体积可小型化，携带方便；受一般障碍物的遮挡影响较小，能够检测到障碍物后的人体目标；并且具有抗多径和窄带干扰能力强的优点，所以采用超宽带脉冲雷达进行数据的采集工作。这里采用的雷达模块是X4M200模块，关于该模块会在之后的文章简单介绍。

在进行人体微动信号提取之前，需要确定人体大致位置，并由此距离单元出的方位信号的相位得到人体微动信号，该位置可由回波信号的距离多普勒图像确定。如图显示对应采样数据下目标的位置在第7个单元位置处，所以微动信号提取第7个单元位置处的相位信息用于微动信号的生成，之后基于微动信号处理得到呼吸心跳的频率信息。

4.1 平滑处理

对微动信号进行平滑处理得到微动信号中低频的呼吸信号分量，再将原信号前去低频分量即可得到高频的心跳信号分量。

可以看出，这样的处理能够有效抑制呼吸信号分量，使得处理得到的信号能够明显显示出心跳的成分，能够实现对心跳频率的估计，但信号的呼吸分量仍然较大，需要进一步去除。

4.2 带通滤波

根据心跳信号频率先验知识0.9-1.6Hz，设计频率范围1-2Hz的带通滤波器，并利用该滤波器对微动信号滤波得到较纯净的心跳的信号，上图是滤波前微动信号的时域、频域表达式，可以看出心跳信号分离效果进一步提升，但是还存在杂波分量。

4.3 MUSIC

考虑带通滤波后的微动信号是随机平稳信号，假设为正弦信号+噪声的模型，并且信号与噪声之间正交，由此可以设计类似于MUSIC的方法估计心跳信号的频率。

由于信号随机平稳，可以由微动信号估计出相关函数：

$R\left ( k \right )=\left\{\begin{matrix} \frac{1}{M}\sum_{n=k}^{M}R_{t}\left ( n \right )R^{*}_{t}\left ( n-k+1 \right )\\ \end{matrix}\right.$

由相关函数构成协方差矩阵，对协方差矩阵进行特征分解得到较小特征值所对应的特征向量，这些向量构成的空间认为是噪声空间，基于频率对信号空间进行搜索，当搜索信号的频率与心跳频率已知，此时信号矢量与噪声空间正交，如果不对应，则搜索的信号向量与噪声空间不正交，由此可以获得对应的谱图：

$P\left ( f \right )=\frac{1}{a'\left ( VV' \right )a}$

其中 $a=\begin{bmatrix} e^{-j2\pi fT_{s}M}& e^{-j2\pi fT_{s}\left ( M-1 \right )} &\cdots & e^{-j2\pi fT_{s}\left ( M-1 \right )}&e^{-j2\pi fT_{s}M} \end{bmatrix}^{T}$ 为搜索信号矢量， $V$ 为噪声空间。

4.4 短时傅里叶变换（STFT）

实际上呼吸心跳信号并非平稳信号，只是依靠FFT以及滤波处理不能很好的分析呼吸心跳特征，需要对微动信号进行时频分析，得到对应的时频特征。短时傅里叶变换的表达式如下：

$X\left ( \tau ,f \right )=\int x\left ( t\right )w\left ( t-\tau \right )e^{-j2\pi ft}dt$

上图是微动信号经过STFT得到的时频图，可以看出心跳信号并非按照正弦运动的平稳信号，而是频率存在波动的非平稳运动。

4.5 小波变换

另一种常见的时频分析方式是小波变换，和短时傅里叶变换不同，其分辨率是变化的，在高频是有较好的时间分辨率，在低频处有较好的频率分辨率，能够分析出信号更有应用价值的特征。表达式如下：

$WT\left ( a,\tau \right )=\frac{1}{\sqrt{a}}\int x\left ( t \right )\psi \left ( \frac{t-\tau }{a} \right )dt$

其中 $a$ 为尺度因子，蕴含频率信息，母小波函数 $\psi \left ( t \right )$ 决定最终小波变换的特性。

上图是微动信号经过小波变换得到的时频图，可以看出心跳信号更加细节的信息（高频信息）。

代码见：《智慧医疗+生物雷达+呼吸心跳检测（包含采集的数据）》

总结

这节内容主要介绍了本科期间的研究方向，通过整理研究内容，一方面进一步加深自身对信号处理在实际应用中的理解，另一方面作为笔记记录本科研究历程，作为之后回顾的范本。本文介绍的信号处理流程虽然简单，个人觉得比较完整，希望能够对相关领域的读者有所启发。转载请附上链接：【杨（_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主

开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

MySQL虚拟列的详细讲解

MySQL运用虚拟列对where条件有函数的的优化MySQL5.7引入了Generated Column，所谓Cenerated Column，就是数据库中的某一列由其他列计算而得。MySQL 5.7中，支持两种Generated Column，即Virtual Generated Column和Stored Generated Column，前者只将Generated Column保存在数据字典