模糊综合评价在实际问题中的应用(案例)
模糊评价问题是要把论域中的对象对应评语集中一个指定的评语或者将方案作为评语集并选择一个最优的方案,本文详细讲解了一级模糊综合评价模型和多级模糊综合评价模型的案例应用,包括如何确定各因素权重,确定隶属函数,得到模糊综合评判矩阵……
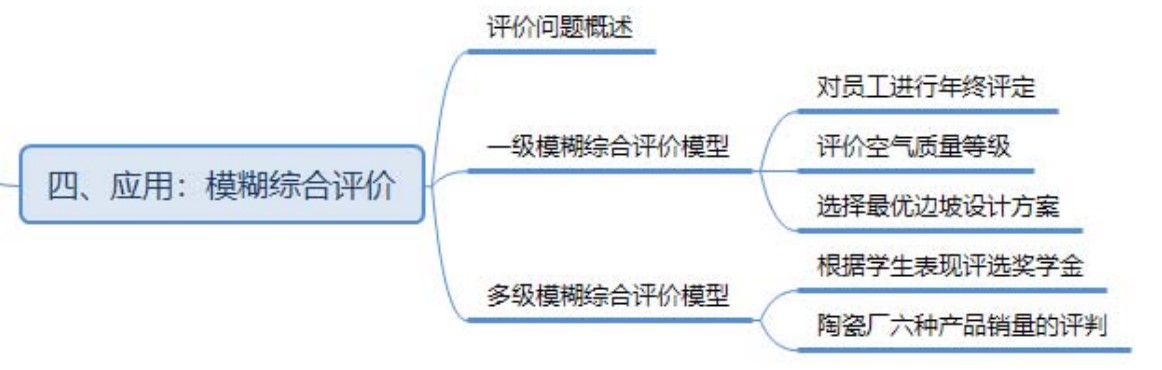
目录
一、概述
模糊综合评价问题是要把论域中的对象对应评语集中一个指定的评语或者将方案作为评语集并选择一个最优的方案。(两个角度)
在模糊综合评价中,引入了三个集合:
①:因素集(评价指标集)U = {u,u
,…,u
} . (这里的U和论域一个符号,但表示的含义有很大差别)
②:评语集(评价的结果)V = {v,v
,…,v
} .
③:权重集(指标的权重)A = {a,a
,…,a
} . (这里的A和集合一个符号,别搞混了)
注:这里的n和m没有任何大小关系,可以取到任意值。
举个栗子:如果要评价一名学生的表现,可令因素集 U = {专业排名,课外实践,志愿服务,竞赛成绩};评语集 V = {优,良,差};权重集 A = {0.5,0.1,0.1,0.3}。(确定权重如果有数据时也可以用熵权法,无数据时可以用层次分析法)
二、一级模糊综合评价模型
案例1. 一级模糊综合评判在人事考核中的应用
在对企业员工进行考核时,由于考核的目的、考核对象、考核范围等的不同,考核的具体内容也会有所差别。有的考核涉及的指标较少,有些考核又包含了非常全面且丰富的内容,需要涉及很多指标。鉴于这种情况,企业可以根据需要,在指标个数较少的考核中,运用一级模糊综合评判,而在问题较为复杂、指标较多时,运用多层次模糊综合评判,以提高精度。
一级模糊综合评判模型的建立,主要包括以下步骤:
(1)确定因素集。对员工的表现,需要从多个方面进行综合评判,如员工的工作业绩、工作态度、沟通能力、政治表现等。所有这些因素构成了评价指标体系集合,即因素集,记为
U = {u,u
,…,u
} (一级模糊评价中,n往往小于或等于5,且指标间相关性不强)
(2)确定评语集。由于每个指标的评价值的不同,往往会形成不同的等级。如对工作业绩的评价有好、较好、中等、较差、很差等。由各种不同决断构成的集合称为评语集,记为
V = {v,v
,…,v
} (评语集中有m个元素,m的大小与n无关,实际问题中 v
,v
,…,v
也可以是方案1、方案2、…、方案m)
(3)确定各因素的权重。一般情况下,因素集中的各因素在综合评价中所起的作用是不相同的,综合评价结果不仅与各因素的评价有关,而且在很大程度上还依赖于各因素对综合评价所起的作用,这就需要确定一个各因素之间的权重分配,它是U上的一个模糊向量,记为
A = [a,a
,…,a
] (式中,
为第i个因素的权重,且满足sum(a
)=1 )
确定权值的方法有很多,如Delphi法、加权平均法、众人评估法等。其中Delphi(德尔菲)法,又称专家调查法:指征求专家意见后再反馈给专家,再次征求意见,直到意见统一为止。显然,如果是在比赛中这种方法无法实现,因此我们在有数据时可以使用熵权法,无数据时使用层次分析法。
(4)确定模糊综合判断矩阵。求出指标 u 对V中各个评语的隶属度,对指标 u
的评判记为
= [
,
,…,
],则模糊综合判断矩阵为:
它是一个从U到V的模糊关系矩阵。
(5)综合评判。如果有一个从U到V的模糊关系 ,那么利用R就可以得到一个模糊变换
,
由此变换,就可得到综合评判结果 B = A·R 。(显然,)
结果分析:综合后的评判可看作是V上的模糊向量,记为 。b
为要评价的对象对评语 i 的隶属度。若
,则表明要评价的对象应划分到评语k这一类。
案例2. 一级模糊综合评判在评价空气质量中的应用
下表给出了大气污染物评价标准:
| 污染物 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 |
|---|---|---|---|---|
| SO | 0.05 | 0.15 | 0.25 | 0.50 |
| TSP | 0.12 | 0.30 | 0.50 | 1.00 |
| NO | 0.10 | 0.10 | 0.15 | 0.30 |
| CO | 4.00 | 4.00 | 6.00 | 10.00 |
| PM | 0.05 | 0.15 | 0.25 | 0.50 |
| O | 0.12 | 0.16 | 0.20 | 0.40 |
今测得某日某地表中这些污染物日均浓度依次为:(0,07,0.20,0.123,5.00,0.08,0.14),各污染物权值确定如下:(0.1,0.2,0.3,0.3,0.05,0.05).试评价当天空气质量等级.
分析:这里各指标权值集合A已给出,综合评判结果 B = A·R,故最关键的就是求模糊综合判断矩阵。在上一讲我们已经用梯形分布求出了SO对应于各评语的隶属度,即为这里模糊综合判断矩阵的R
,同理我们可求出R
,即可得到模糊综合判断矩阵R,代入计算即得到综合判断结果B = (0.252,0.478,0.27,0). 因此这一天的空气质量等级为二级。
案例3. 模糊综合评价选择最优的方案
某露天煤矿有五个边坡设计方案,其各项参数根据分析计算结果得到边坡设计方案的参数如下表所示:
| 项目 | 方案一 | 方案二 | 方案三 | 方案四 | 方案五 |
|---|---|---|---|---|---|
| 可采矿量/万吨 | 4700 | 6700 | 5900 | 8800 | 7600 |
| 基建投资/万元 | 5000 | 5500 | 5300 | 6800 | 6000 |
| 采矿成本 /(元/吨) | 4.0 | 6.1 | 5.5 | 7.0 | 6.8 |
| 不稳定费用/万元 | 30 | 50 | 40 | 200 | 160 |
| 净现值/万元 | 1500 | 700 | 1000 | 50 | 100 |
据勘探,该矿探明储量8800吨,开采总投资不超过8000万元,试做出各方案的优劣排序,选出最佳方案。
解:首先确定隶属函数(隶属函数不唯一,只要合理(说是根据专家建议或他人写的文章)就行)
(1)可采矿量的隶属函数(偏大型)
因为勘探的地质储量为8800吨,故可用资源的利用函数作为隶属函数:
(2)基建投资的隶属函数(偏小型)
投资约束是8000万元,所以
(3)采矿成本的隶属函数
根据专家意见,采矿成本 a 元/吨为低成本,a
元/吨为高成本,故

(4)不稳定费用的隶属函数(偏小型)
(5)净现值的隶属函数(偏大型)
取上限15(百万元),下限0.5(百万元),采用线性隶属函数 .
注:从隶属函数的构造可以看出,五个因素的隶属函数均经过了正向化处理(类似Topsis中的概念),即隶属度越大,说明越有利。
这样我们就可得到单因素评判矩阵
根据专家评价,诸因素在决策中占的权重为 A = (0.25,0.20,0.20,0.10,0.25),于是得诸方案的综合评价为 B = A·R = (0.7435,0.5919,0.6789,0.3600,0.3905)
由此可知:方案一最佳,方案三次之,方案四最差。(如果没有专家怎么办?用熵权法!)
三、多级模糊综合评价模型
Q:为什么要引入“多级”?
A:当因素集中元素较多时,因素集指标间的相关性可能很强,这时我们可对因素集指标进行分类操作,分类后可以简化我们的计算。比如,当有10个指标时,如果想知道各自的权重,则我们需两两进行比较,情况非常多!但如果我们先进行分类,那么要考虑比较的指标就变少了。
案例4:评价学生的表现并作为奖学金的评判标准.
因素集 U = {专业课成绩,非专业课成绩,国家竞赛成绩,省级竞赛成绩,校级竞赛成绩,国家级荣誉奖项,省级荣誉奖项,校级荣誉奖项,志愿服务时长}。我们可先进行归类

假设评语集 V = {一等奖学金V1,二等奖学金V2,无奖学金V3};
若投票得到 , (即模糊统计法,10个评委投票得到),其中0.8的含义为这位同学的专业课成绩对于V1的隶属度为0.8,即有8名评委认为可获一等奖学金,2名评委认为可获二等奖学金;同理可得到R2,R3,R4;设A1,A2,A3,A4分别为求得的对应权重,则模糊综合评判矩阵:
综合评判结果 B = A·R,最后按最大隶属度原则即可确定相应评语或等级。
案例5. 三级模糊综合评价模型




Over!!!

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)