红黑树详解(下)(红黑树的删除操作)
红黑树的删除和对应修复操作详解。
上篇中,我们学习了红黑树的性质,并掌握了红黑树的查找和插入操作。接下来,我们将对红黑树的删除操作展开研究。
红黑树的删除操作
当然,我们先要根据需要删除的键(key)寻找目标节点的位置。这和二叉查找树的查找过程一样。
如果找不到目标节点,说明删除目标已经不在树上了,不用做任何操作。
如果找到了要删除的节点,那么我们将研究如何删除这个节点。
乍一想,节点可能有0、1、2个孩子,可能是红色或黑色,孩子的颜色也千变万化,看似难以入手。但是,我们可以把所有的情况分成三大类:

- 删除目标没有孩子
(注:我们用黄色标记出想要删除的节点)

- 删除目标只有一个孩子

- 删除目标有两个孩子
聪明的你一定会觉得,第1种情况是最好处理的。虽然你依旧不知道该怎么处理,但直觉告诉你,它就是比后面两种好处理。
如果你对二叉平衡树的删除有所了解,应该知道,在执行删除操作时,可以通过一些简单的变换,转移删除目标。没看懂?没事,我们用一个例子来看。
因为情况1看上去比较简单,就先放在这里不动。
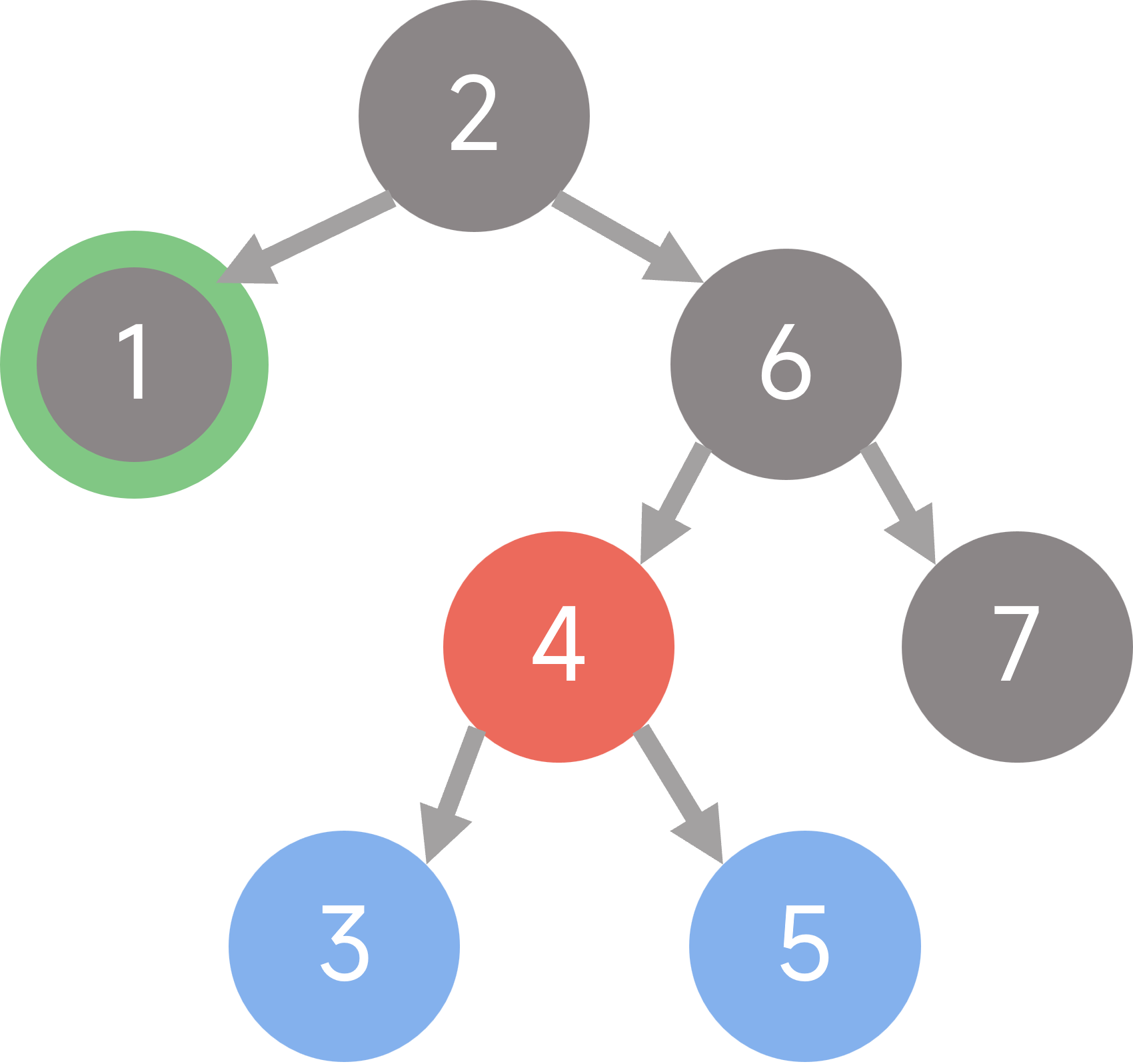
对于情况2,我们寻找一张更复杂的图来分析:

如图,我们想删除节点12. 它有1个孩子。由于它有右孩子,它的后继节点一定是在它的子树里。从子树中寻找它的后继节点(节点13),将两个节点交换,得到如下情况:

节点13来到了节点12所在的位置。此时,由于节点12被替换到了子树中,整棵树违背了二叉查找树的性质。但是没关系,毕竟节点12是要被删除的,删掉后不违背就行。
这样,我们将原来想要删除的节点移动到了更靠下的位置。
寻找现在的节点12的后继节点,进行交换,得到下图:

我们将需要删除的节点移动到了最底端。现在,它是一个没有孩子的节点(叶节点),属于我们认为比较好处理的情况1. 对于违背的平衡二叉树的性质,如果你直接把这个节点抹掉,会发现,这棵树不再违背平衡二叉树的性质。
以上操作中,我们将移除拥有1个右孩子的节点转换成移除一个叶节点。如果删除目标是一个只有左孩子的节点,那么寻找其前驱节点来交换就行了。
不难看出,情况3也可以用同样的方式转换成情况1. 现在,我们只需要对情况1展开研究就行了,因为情况2和情况3都可以优雅地转换成情况1.
继续之前,我们回顾一下红黑树的五大性质:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色的。
- 如果一个节点是红色的,那么它的父节点一定是黑色的(即:一条边的两端不能同时为红色)。
- 红色节点要么没有孩子,要么有两个黑色的孩子。
- 从根节点到每个叶节点的路径中,黑色节点的数量(计数时包含叶。但是否含根不影响结果)一定是一样的。
对“情况1”的深入分析
删除目标的颜色有两种可能性:
- 红色
- 黑色
如果删除目标是红色,没有什么可讨论的,删了就行。如下图:

如图,当我们想要删除节点8时,直接将它删了就是。因为它本身是红色的叶子节点,没有孩子,删除它,并不会破坏任何一条性质。所以,没必要做其他调整。因此,我们只需要研究删除目标是黑色的叶节点的情况。
如果要删除的是黑色的叶节点,比如这样:

删除节点8,一定会违背红黑树的性质。此处,显然同时违背了性质4和性质5. 如果节点8的父亲是黑色的,那么它可以不违背性质4,但是性质5一定是会被违背的。因此,对于删除目标是黑色叶节点的情况,在删除后,一定要做修复操作。
我们可以将删除黑色叶节点时可能遇到的情况分成以下9种(考虑到对称性,每对轴对称的情况我们只研究其中的一个。另一个请聪明的你自行推导):
情况1:父节点是红色的。
因为父节点是红色,那么兄弟节点一定存在,并且一定是黑色的。局部图如下所示:

其中,节点1是要删除的节点。父节点是节点2. 兄弟节点是节点4. 蓝色的节点3和节点5都是可以存在也可以不存在的。但是,如果他们存在,那么一定红色的,不然一定会违背性质5(假如节点3是黑色,那么从节点2到节点1,经过了1个黑色节点。但是,从节点2到节点3,经过了2个黑色节点。在这个局部违背了性质5,那么整棵树一定违背了性质5).
我们需要根据兄弟孩子的不同情况分别做处理。
情况1.1:兄弟节点有2个红色的孩子
如图所示:

删除节点1后,节点2的左侧缺少黑色节点,导致违背红黑树性质。我们需要想办法将节点向左移动,试图填补空缺。
尝试对父节点做左旋,得到如下图:

删掉节点1,然后将节点4(兄弟)、节点2(父亲)和节点5(兄弟的右孩子)反色,得到如下:

你会发现,如果修复前的局部没有违背红黑树的性质,那么修复后是不违背红黑树的性质的。如此操作完成后,红黑树已经恢复,不需要再对其他部分进行更改。
情况1.2:兄弟节点只有左孩子
这个左孩子一定是红色的,不然会违背性质5. 局部如图所示:

去掉节点1后,我们尝试重新排列节点2、3、4,试图在保持二叉查找树的性质的前提下,不再破坏红黑树的性质。我们发现,如果能实现下图排布,就可以了:

那么,如何将之前的局部变成我们希望的样子呢?这一定难不倒聪明的你。借助旋转和变色操作,可以很轻松地完成:
- 对兄弟节点做右旋转,变成这样:

- 对父节点做左旋,得到如下(已将节点1略去):

- 对父节点和兄弟节点做反色操作,即可。
情况1.3:兄弟节点只有右孩子
这个孩子一定是红色的。如图:

尝试对节点2、4、5重新排布,可以发现,只要排成下图这样,就可以恢复红黑树的性质:

这个操作并不难,只需要将父节点做左旋,然后对所有节点做反色,就可以了。
聪明的你一定想问,这种情况下,如果不做反色,是否可以呢?当然是可以的!如果不做反色,局部根节点是黑色的,不可能与它的父亲一起违背性质4. 同时,从局部的根到叶子依旧是只需要经过1个黑色节点,不会违背性质5.
情况1.4:兄弟节点没有孩子
就像这样:

如果我们简单地将父节点和兄弟节点的颜色交换一下,变成这样:

你看,简单地改了改,就完成了修复。是不是非常简单!
至此,“父节点是红色的”已经探讨完毕。这里,我们一直假定删除目标是父亲的左孩子。如果删除目标是父亲的右孩子,情况是轴对称的。只需要将每步操作中的“左”改成“右”,“右”换为“左”,就解决了。这一定难不倒聪明的你。
是时候研究当父节点为黑色时,是什么样子了。
情况2:父节点是黑色的
因为删除节点存在,父节点是黑色,我们可以保证兄弟节点存在(不然会违背性质5)。但是,我们不知道兄弟是什么颜色,也不知道当兄弟是红色时,它的孩子是否还有节点。属实烦人…
情况2.1:兄弟节点是红色的
这时,兄弟节点必须有2个孩子(否则会破坏性质5),并且2个孩子都是黑色的(不然会破坏性质4)。如图:

(其中蓝色表示可能不存在的节点。但是,在此情况下,一旦存在,一定是红色的)
删除节点1后,我们对其他节点尝试重新排布。似乎没有什么固定的公式,但可以知道的是,我们需要想办法把节点往左边倾斜,以此填补空位。最终我们找到这样的方案:
先对父节点(节点2)做左旋,得到如下:

之后,再对父节点(节点2)做左旋,得到如下:

对父节点做反色,得到如下:

对比删除前的模样,你会发现,我们好像已经完成了修复。
诶等等,如果节点3存在,会怎么样?
你看,根据之前的分析,节点3如果存在,就一定是红色的。这时,节点2和节点3连在一起,违背了性质4. 怎么办?
回忆插入过程,我们其实已经对这种情况做过处理了。我们只需要将节点3视为新插入的节点,然后进行插入步骤中对“连续红色节点”的修复操作即可。
情况2.2:兄弟节点是黑色,并且拥有2个孩子
这两个孩子一定是红色的。如图:

尝试对节点2、3、4、5重新排布,试图修复红黑树的性质。最终,我们发现,如果四个节点能排成下图这样,就可以了:

这个转换过程十分简单:
- 对兄弟做右旋
- 对父亲做左旋
- 对兄弟的左孩子做反色
情况2.3:兄弟节点是黑色,并且只有一个左孩子
再看一眼情况2.2,你会发现,节点5是否存在似乎并不影响整个过程。因此,如果兄弟的右节点不存在,我们不需要单独考虑,继续按照情况2.2的同款操作进行修复即可。
情况2.4:兄弟节点是黑色,并且只有一个右孩子
这个孩子一定是红色的。情况如图:

我们发现,只用对父节点做左旋,然后对兄弟的右孩子进行反色,即可。结果如下:

情况2.5:兄弟节点是黑色,并且没有孩子
情况如下:

删除节点1后,变成下图这样:

你会发现,无论如何调整,都无法恢复红黑树的性质。毕竟现在只有两个节点,为满足性质4,必须将其一染红,但这样又会违背性质5(之前从局部的根到叶子需要经过2个黑色节点,修改后只剩1个了)。因此,我们无法仅在这个局部完成修复。
这该怎么办呢?但是,虽然我们无法在局部保证整棵树的平衡,我们可以先做到局部平衡,然后向爷爷求助。
我们将上图中的节点3染成红色,得到如下情况:

至此,我们保证这个小局部没有违背红黑树的性质。同时,由于局部根节点的颜色没有变,我们不会给爷爷添新的麻烦(如果爷爷是红色,我们的局部根节点从黑色变成红色,那么明显会为爷爷带来更多的麻烦。这么做是不好的,不符合尊老爱幼的传统美德)。
这时,我们转换了问题:修复失衡的黑色节点。即:在节点3的父亲看来,如果往其另一个孩子的方向一路走到叶子,会经历n个黑色节点,那么往节点3这个方向一路走到叶子,会经历n-1个节点。
我们希望英明的爷爷可以通过一些操作,使得从两个方向走到叶节点都经过n个节点。
当然,如果爷爷办不到的话,希望他能让往两个方向走到叶节点都经过n-1个节点,这样从它的角度看,维持了一个新的局部平衡,然后再向它的更上级求助。
接下来的分析中,我们将诸如节点3这样维持了局部平衡,但是跟父节点的另一棵子树对比,到叶子的路径少一个根节点的节点,称为失衡节点。
后续在提到父节点、兄弟节点等时,如无特殊说明,我们说的是失衡节点的爸爸和兄弟。
修复失衡节点
首先,失衡节点一定是黑色的。如果它是红色的,只需要变为黑色,失衡问题就不再存在了。
对于失衡节点,我们需要讨论它的父亲、讨论它的兄弟、讨论它的兄弟的孩子…情况很多,我们慢慢看。
情况1:父节点是红色
显然,失衡节点有一个黑色的兄弟。这个兄弟必须有孩子,并且当兄弟的孩子是红色时,红色孩子必须也有孩子。
**为什么?**因为,如果没有,那么从父节点往兄弟走,只需要经过1个黑色节点即可到达叶子(不含父节点)。那么,往失衡节点方向走,只需要经过 1-1=0 个黑色节点就能到到叶子。然而,失衡节点本身是黑色的,和上面那个0矛盾了。
情况1.1:兄弟的左孩子是黑色
如图:

图中,绿圈标记的是失衡节点,蓝色的是可有可无的节点。失衡节点可以有子树,节点3和节点5也可以有子树。我们需要保证操作过后,不影响到它们。不然会为自己带来更多麻烦。
注意,如果我们不改变局部“叶”节点的颜色,或者将红色改成黑色,并且让它们在变动后依旧是局部的“叶”节点,就不会使得它们的子树破坏红黑树性质。
对于上图的情况,我们需要想办法让从局部根节点往节点1走的时候,多经过一个黑色节点。往节点3和节点5方向走的时候,经过的黑色节点不能比之前少(当然也不能比之前多)。经过对节点们的调整,我们得到如下排法:

从根往每个“叶”走一下,你会发现,没有新违背性质,并且往节点1走的时候可以多经过一个黑色节点。如此,我们完成了对失衡情况的修复。聪明的你一定一下就看出了修复操作:对父节点做左旋。
情况1.2:兄弟的左孩子是红色,兄弟的右孩子是黑色
如图:

我们交换一下父节点和兄弟的颜色,得到如下情况:

如果不考虑性质4,那么修复过程已经完成了。现在,我们仅仅违背了性质4. 这很好办呀,因为我们已经研究过怎么处理“连续红色节点”问题了。对节点3修复“连续红色节点”问题即可。
情况1.3:兄弟节点的两个孩子都是红色的
如图:

我们进行以下4步操作:
- 将父亲染成黑色
- 将兄弟染成红色
- 将兄弟的右孩子染成黑色
- 对父亲做左旋
得到如下:

修复完毕。
至此,父节点是红色的情况,我们已经讨论完了。
情况2:父节点是黑色
这时,兄弟节点一定存在,但是颜色未知。
情况2.1:兄弟节点为黑,兄弟的孩子都是黑色的
如图:

黑色节点太多了,怎么弄都无法完成修复。这时,我们可以将兄弟设成红色,以此来完成局部平衡,然后向上级求救。
兄弟节点设为红色后,如下:

我们完成了局部的修复。这时,将父节点标记为新的失衡节点,然后求救于爷爷即可。
情况2.2:兄弟节点为黑,兄弟节点的右孩子为红
如图:

(图中蓝色表示颜色未知,但是不影响)
我们对父节点做左旋,然后将兄弟节点的右孩子染成黑色,即可完成修复。如下图:

情况2.3:兄弟节点为黑色,兄弟节点的左孩子为红色,兄弟节点的右孩子为黑色
如图:

执行以下操作,即可完成修复:
-
将兄弟的左孩子染成黑色
-
对兄弟做右旋
-
对父亲做左旋
结果如图:

情况2.4:兄弟节点为红色
那么兄弟节点一定有两个黑色的孩子。
如图:

我们进行以下操作:
- 将父亲染成红色
- 将兄弟染成黑色
- 对父亲做左旋
得到如下:

诶呀,好像并没有修复成功。但是,观察节点1、2、3组成的局部,是不是很熟悉?它正是前面已经研究过的情况1. 按照情况1中的三种子情况分类处理即可。
至此,红黑树的删除操作已经研究完毕。再次说明,我们只研究了目标节点在靠左位置的情况。对应的轴对称情况,只不过是轴对称一下,聪明的你一定能很轻松地自行完成。
或许你会提出两个疑问。
疑问1:上面那个不断求救于父亲的过程,如果每一步都要求救,最终会在什么时候停止呢?
答:处理过程中,“失衡节点”会不断向根靠近。当某一次处理完毕后,“失衡节点”正是根节点了,我们就不需要做任何处理,直接结束就行。毕竟我们已经完成了对“失衡节点”下方的局部平衡,当它正是根节点时,就相当于整棵树已经平衡了(这个平衡指的是满足红黑树的性质5,且不破坏其他性质)。
疑问2:我们在分情况时,似乎默认了父节点的存在,这样做是否有问题?
答:当然,父节点可以不存在。但是,因为我们已经将问题简化成了“黑色的叶子节点”,一旦该节点没有父亲,它一定是这棵树上的唯一一个节点。我们不需要多加思考,直接删除即可。
结语
读到这里,你已经完成了红黑树的基本学习。你了解了什么是红黑树,学习了红黑树的性质,学会了红黑树的查找、插入、删除操作。上世纪的智者将一个个伟大的火把交到我们手中,我们要牢牢握住,并用它照亮前方的路,点燃远方的灯。如果你希望学习如何用代码向计算机讲述红黑树结构,欢迎继续阅读后续文章。
代码
参考文献
Wikipedia.Red–black tree
安卓大叔.30张图带你彻底理解红黑树
振兴.红黑树深入剖析及Java实现
政采云前端团队.通俗易懂的红黑树图解(下)
程序员景禹.图解:红黑树删除篇(一文读懂)
Cailiang.数据结构:红黑树的删除
nguliu.红黑树删除节点——这一篇就够了
百度百科.红黑树

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)