LDA主题模型及Python实现
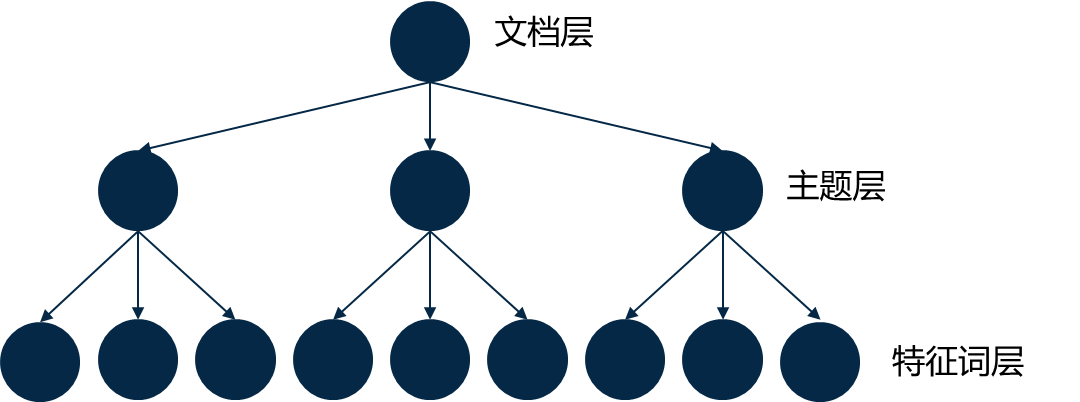
LDA(Latent Dirichlet Allocation)是一个三层贝叶斯概率模型,包括词、主题和文档三个层次。它可以将文档集中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。
主题模型是用于发现文档集合中隐含主题的统计模型,主题可以定义为“文档集中具有相同词境的词的集合模式”,比如,将“健康”、“病人”、“医院”、“药品”等词汇集合成“医疗保健”主题,将“农场”、“玉米”、“小麦”、“棉花”、“播种机”、“收割机”等词汇集合成“农业”主题。
主题模型克服了传统信息检索中文档相似度计算方法的缺点,并且能够在海量互联网数据中自动寻找出文字间的语义主题。
其中最著名的是潜在狄利克雷分配(Latent Dirichlet Allocation, LDA)模型。
一、LDA主题模型概述
LDA(Latent Dirichlet Allocation)是一个三层贝叶斯概率模型,包括词、主题和文档三个层次。它可以将文档集中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。

LDA的实质是利用文本的特征词的共现特征来挖掘文本的主题。
词汇共现关系,指的是在特定语境、特定范围内,两个或多个词汇在文本中一起出现的现象。通过分析词汇的共现关系,可以捕获词汇之间的语义联系和依赖关系,这对于理解文本的意义、构建语义网络以及进行复杂的语言模型训练等任务至关重要。例如:“新型冠状病毒导致的疫情迅速蔓延。全球多国采取封锁措施。”在这句话里,“新型冠状病毒”与“疫情”、“蔓延”、“封锁”和“全球”可能会被标记为共现,因为它们在相近的文本范围内出现,揭示了疫情相关的主题和背景。
二、LDA主题模型原理
2.1 LDA核心思想
人类是怎么生成文档的呢?LDA的作者在原始论文中给了一个简单的例子。比如假设事先给定了这几个主题:Arts、Budgets、Children、Education,然后通过学习训练,获取每个主题Topic对应的词语。如下图所示:

然后以一定的概率选取上述某个主题,再以一定的概率选取这个主题下的某个单词,不断的重复这两步,最终生成如下图所示的一篇文章(其中不同颜色的词语分别对应上图中不同主题下的词):

生成的文档里面的每个词语出现的概率为:
P
(
词语
∣
文档
)
=
∑
P
(
词语
∣
主题
)
×
P
(
主题
∣
文档
)
P(\text{词语}|\text{文档}) = \sum P(\text{词语}|\text{主题}) \times P(\text{主题}|\text{文档})
P(词语∣文档)=∑P(词语∣主题)×P(主题∣文档)
LDA是基于这样的假设:文档是由一系列的主题以一定比例混合而成的,而每个主题则是由一系列特定的词以一定概率分布组成的。通俗来讲,也就是作者先确定这篇文章的几个主题,然后围绕这几个主题遣词造句,表达成文,生成各种各样的文章。
而LDA就是要试图通过学习文档-主题分布和主题-词分布来反推每篇文档的潜在主题结构,也就是说,用计算机推测分析网络上各篇文章分别都写了些啥主题,且各篇文章中各个主题出现的概率大小是啥。
2.2 LDA模型中文档生成过程
- 对于文档 d d d ,LDA模型首先从Dirichlet分布中抽取一个主题分布 θ d \boldsymbol{\theta}_d θd,这个分布由参数 α α α 控制。
- 根据文档 d d d 的主题分布 θ d \boldsymbol{\theta}_d θd,从文档 d d d 对应的主题多项式分布中抽取一个主题 z d , n z_{d,n} zd,n。
- 从Dirichlet分布中抽取主题 z d , n z_{d,n} zd,n 对应的词语多项式分布 ϕ z d , n \boldsymbol{\phi_{z_{d,n}}} ϕzd,n ,这个分布由参数 β β β 控制。
- 根据选定的主题 z d , n z_{d,n} zd,n对应的词语多项式分布 ϕ z d , n \boldsymbol{\phi_{z_{d,n}}} ϕzd,n中选择一个词 w d , n w_{d,n} wd,n 。
过程如图:

2.3 LDA模型主题分析过程
LDA主题模型具体的实现就是确定出参数
(
α
,
β
)
(α,β)
(α,β),分析过程如图:

在实际应用中,我们可以直接调用LDA主题分析的包。
三、Python应用
3.1 文本预处理
在用 Python 进行 LDA 主题模型分析之前,我们先对文档进行了去停用词、剔除特殊符号和分词处理。
import pandas as pd
import jieba
import re
# 加载EXCEL表
file_path = r"news_content.xlsx"
df = pd.read_excel(file_path)
# 自定义函数:对内容进行分词,过滤停用词
def word_cut(content):
# 添加自定义词典后的分词(此处假设自定义词典路径为 user_dict.txt,需要预先准备好)
user_dict_path = r"user_dict.txt"
jieba.load_userdict(user_dict_path)
# 剔除特殊符号
content = re.sub(u'\n|\\r', '', content) # 剔除换行符和回车符
content = re.sub(r'[^\w\s]', '', content) # 剔除非中文、非字母和非数字的字符
content = re.sub(u'[^\u4e00-\u9fa5]', '', content) # 剔除所有非中文字符
# 加载停用词表
stopwords = set()
with open(r"cn_stopwords.txt", 'r', encoding='utf-8') as f:
for line in f:
stopwords.add(line.strip())
# 用jieba分词
words = jieba.cut(content)
filtered_words = [word for word in words if word not in stopwords]
return (" ").join(filtered_words)
# 应用函数,对每条评论进行分词,过滤停用词
df['content_cutted'] = df['content'].apply(word_cut)
# 查看结果
print(df[['content', 'content_cutted']].head())
# 保存结果
output_path = r"news_content_processed.xlsx"
df.to_excel(output_path, index=False)
3.2 sklearn实现LDA主题提取
LDA 分析可以调用 sklearn 库和 Gensim 库,下面的分析我们用 sklearn 库来实现。
- 导入 sklearn 库
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
-
将文本数据转换为词频(term frequency)向量矩阵。
文本向量化没有选择TF-IDF向量的原因有以下几点:
- LDA 关注的是词的出现频率(在文档内),而不是词在文档集合中的分布情况。
- 在 LDA 的上下文中,高频词(如某些专业术语或特定领域常用词)可能正是定义主题的关键,使用 TF-IDF 可能会导致这些词的重要性被不恰当地降低。
- 一些经验表明,使用纯粹的词频(TF)作为特征输入到 LDA 模型中,通常能够更好地捕捉主题的语义结构。
# 提取特征词数量
n_features = 1000
# 将文本数据转换为词频向量矩阵
tf_vectorizer = CountVectorizer(strip_accents='unicode', # 去除文本中的重音符号
max_features=n_features, # 提取的最大特征数(词语数)为1000
stop_words='english', # 移除所有英文停用词
max_df=0.5, # 忽略在超过50%的文档中出现的词语
min_df=10) # 词语至少在10个文档中出现才能被考虑,去除罕见的词语,避免过拟合
tf = tf_vectorizer.fit_transform(df.content_cutted)
-
训练 LDA 模型,识别文本中的潜在主题。在LDA提取主题前,我们要先给定主题数量。确定最优主题数的方法有:
- 经验和可视化结合法:通过可视化工具查看不同主题数下的关键词分布,结合已有文献或个人经验,进行反复调试,观察主题聚类效果,进行人工判断,从而确定主题个数。
- 困惑度:在 sklearn 的 LDA 实现中,可以直接通过 .perplexity() 方法来计算、评估不同主题数下 LDA 模型的困惑度。通常,困惑度越低,模型的预测性能越好。
- 似然分数:它直接反映了模型对数据的拟合程度。对数似然值越高,表示模型与数据的契合度越好。与困惑度一样,可以针对不同主题数计算对数似然值,选择最高的一个。
下面的代码,我们将结合以上三种方法来确定最优主题数量。除以上三种方法外,常用的方法还有计算一致性和主题间相似性。
# 使用了LDA模型来识别文本数据中潜在的主题
# 定义主题数
n_topics = 8
# LDA模型初始化
lda = LatentDirichletAllocation(n_components=n_topics, max_iter=50, # 指定模型应该识别的主题数和算法的最大迭代次数
learning_method='batch', # 指定学习方法,'batch' 方法通常更稳定
# 'batch' 意味着使用所有的数据点来更新模型的参数
# 相对于 'online' 方法(逐步使用小批量数据更新模型)
learning_offset=50, # 用于稳定在线学习的早期迭代
# doc_topic_prior=0.1, # 文档-主题先验,即α值
# topic_word_prior=0.01, # 主题-词先验,即β值
random_state=0) # 设置一个随机种子用于结果的可复现性
# 通过fit方法训练模型,找到最佳的文档-主题和主题-词分布
lda.fit(tf)
# 提取每个主题的前 n_top_words 个最重要的词语
# 构建函数,从主题模型中提取每个主题的前 n_top_words 个最重要的词语
def print_top_words(model, feature_names, n_top_words):
tword = []
# 遍历模型的每个主题
for topic_idx, topic in enumerate(model.components_): # topic_idx 是主题的索引,topic 是一个包含词权重的数组
print("Topic #%d:" % topic_idx)
topic_w = " ".join([feature_names[i] for i in topic.argsort()[:-n_top_words - 1:-1]]) # 返回基于权重排序后的词语索引数组
# 权重最大的词语索引排在前面
tword.append(topic_w)
print(topic_w)
return tword
# 设置每个主题中要提取的重要词语数量
n_top_words = 25
# 获取所有特征词
tf_feature_names = tf_vectorizer.get_feature_names()
# 调用函数,从主题模型中提取每个主题的前 n_top_words 个最重要的词语
topic_word = print_top_words(lda, tf_feature_names, n_top_words)
# 输出每篇文章对应主题
import numpy as np
# 将tf矩阵转换为数组,行代表文档,列代表主题,使用 LDA 模型计算文档属于对应主题的概率
topics = lda.transform(tf)
# print(topics[0])
# 确定每个文档最主要的主题
topic = []
for t in topics:
topic.append(list(t).index(np.max(t)))
df['topic'] = topic
print(df.head())
# 导出为EXCEL表
df.to_excel(r"data_topic.xlsx", index=False)
将结果可视化,以判断是否为最优主题数。
# 结果可视化
import pyLDAvis.sklearn
pic = pyLDAvis.sklearn.prepare(lda, tf, tf_vectorizer)
pyLDAvis.save_html(pic, r"topic.html")
计算困惑度和似然分数,以帮助确定最优的主题数。
import matplotlib.pyplot as plt
plexs = []
scores = []
n_max_topics = 16
for i in range(1, n_max_topics):
lda = LatentDirichletAllocation(n_components=i, max_iter=50,
learning_method='batch',
learning_offset=50,random_state=0)
lda.fit(tf)
plexs.append(lda.perplexity(tf)) # 计算困惑度
scores.append(lda.score(tf)) # 计算似然分数
# 困惑度可视化
n_t = 15 # 区间最右侧的值。注意:不能大于n_max_topics
x = list(range(1, n_t))
plt.plot(x, plexs[1:n_t])
plt.xlabel("number of topics")
plt.ylabel("perplexity")
plt.show()
# 似然分数可视化
n_t = 15 # 区间最右侧的值。注意:不能大于n_max_topics
x = list(range(1, n_t))
plt.plot(x, scores[1:n_t])
plt.xlabel("number of topics")
plt.ylabel("score")
plt.show()
困惑度可视化图:

似然分数可视化结果:

由前面的分析,我们知道,困惑度是越低越好的,那么我们应该选择主题越多越好,但是,显然这是不对的。因为当主题太多时,我们的模型已经过拟合了。我们发现当主题个数超过8时,模型的困惑度就不再大幅度下降,而是呈缓慢下降趋势。所以,我们的最优主题个数应该为8。
再结合主题可视化结果,也可以看到,当主题个数为10时,topic4 几乎为 topic2 的纯子集,所以,选择8个主题时,分类效果比较好。
主题个数为8时:

主题个数为10时:


开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)