【数电笔记】加法器、减法器

半加法器、全加器、进位传播加法器（行波进位加法器、先行进位加法器、前缀加法器）、减法器的原理和实现。

seh_sjlj

7815人浏览 · 2022-10-24 17:50:29

seh_sjlj · 2022-10-24 17:50:29 发布

文章目录

一、半加法器（Half Adder）
二、全加器（Full Adder）
三、进位传播加法器（Carry Propagate Adder, CPA）
四、减法器
参考书目

一、半加法器（Half Adder）

输入： $A$ 、 $B$ （代表相加的两个位）
输出： $S$ （代表 $A$ 与 $B$ 的和）、 $C_{\text{out}}$ （进位）

计算公式：

$S=A\oplus B$ （ $A$ 和 $B$ 的异或）
$C_{\text{out}}=AB$ （ $A$ 和 $B$ 进行与操作，仅当 $A$ 、 $B$ 同时为 $1$ 时才进位）

图示：
半加法器

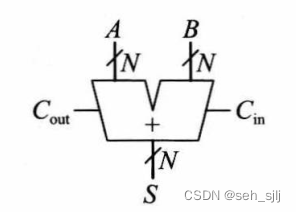
二、全加器（Full Adder）

输入： $A$ 、 $B$ （相加的两个位）、 $C_{\text{in}}$ （上一位的进位）
输出： $S$ 、 $C_{\text{out}}$

功能：计算 $A+B+C_{\text{in}}$ ，输出 $S$ 和进位 $C_{\text{out}}$

计算公式：

$S=A\oplus B\oplus C_{\text{in}}$ （注意 $A\oplus B$ 本质上等于 $(A+B)\ \text{mod}\ 2$ ）
$C_{\text{out}}=AB+AC_{\text{in}}+BC_{\text{in}}$ （在 $A,B,C_{\text{in}}$ 中至少有两个为 $1$ 则需进位）

图示：
全加器

三、进位传播加法器（Carry Propagate Adder, CPA）

输入：两个 $N$ 位输入 $A, B$ ；一位进位 $C_{\text{in}}$
输出：一个 $N$ 位输入 $S$ ；进位 $C_{\text{out}}$
实现方法：行波进位加法器、先行进位加法器、前缀加法器
图示：
进位传播加法器

1. 行波进位加法器（Ripple-Carry Adder）

构造方法：把 $N$ 个全加器串联起来，一级的 $C_{\text{out}}$ 作为下一级的 $C_{\text{in}}$
缺点：当 $N$ 较大时运算速度会慢下来
延迟： $t_{\text{ripple}}=Nt_{\text{FA}}$ ，其中 $t_{\text{FA}}$ 为全加器的延迟
图示：
行波进位加法器

2. 先行进位加法器（Carry-Lookahead Adder, CLA）

特点：把加法器分成若干块，在每块一得到输入进位时就快速算出此块的输出进位。例如， $32$ 为加法器 $=$ $8\times4$ 位的块
原理：

进位分两种：（考虑第 $i$ 位，也叫第 $i$ 列）
- $A_i$ 和 $B_i$ （均为 $1$ 时）本身就能产生进位——产生进位，令 $G_i=A_iB_i$
- $A_i$ 或 $B_i$ 为 $1$ ，且在有上一位的进位 $C_{i-1}$ 时才能进位——传播进位，令 $P_i=A_i+B_i$
因此第 $i$ 位的进位 $C_i=A_iB_i+(A_i+B_i)C_{i-1}=G_i+P_iC_{i-1}$
推广到多位构成的块：
- 一个块在不考虑进位输入的情况下也能发生进位——产生进位
- 一个块在有进位输入时才能进位——传播进位
定义 $G_{i:j}$ 和 $P_{i:j}$ 为从第 $i$ 到第 $j$ 为的产生和传播信号
- 一个块产生进位（ $G_{i:j}=1$ ）的条件：最高位产生进位，或最高位传播进位且前一位产生进位。设块的位数是 $i : 0$ ，则有递推公式 $G_{i:0}=G_i+P_iG_{i-1:0}$ 。当 $i = 3$ 时有 $G_{3:0}=G_3+P_3(G_2+P_2(G_1+P_1G_0))$
- 一个块传播进位（ $P_{i:j}=1$ ）的条件：输入到块中的进位 $C_{j-1}$ 能经过块传到 $C_i$ ，这就要求进行环环相扣的进位（连锁反应），即块中的每一列都能传播进位。则 $P_{i:0}=P_iP_{i-1}\cdots P_iP_0$
因此块的生成和传播信号可由 $C_{j-1}$ 、 $G_{i:j}$ 和 $P_{i:j}$ 快速算出： $C_i=G_{i:j}+P_{i:j}C_{j-1}$

延时： $pg_block + ( N k − 1 ) t AND_OR + k t FA t_{\text{CLA}}=t_{\text{pg}}+t_{\text{pg\_block}}+\left(\frac Nk-1\right)t_{\text{AND\_OR}}+kt_{\text{FA}}$

$t_{\text{pg}}$ ：计算 $P_i$ 和 $G_i$ 所需要的时间（即单独的 $\text{AND}$ 或 $\text{OR}$ 门的延时）
$pg_block t_{\text{pg\_block}}$ ：计算 $P_{i:j}$ 和 $G_{i:j}$ 所需要的时间
$AND_OR t_{\text{AND\_OR}}$ ：在 $k$ 位CLA块中计算 $C_{\text{out}}=G_{i:j}+P_{i:j}C_{\text{in}}$ 的时间（共有 $\frac Nk$ 个 $C L A$ 块，但位数最高的块不需要进位给下一个块，所以这个块直接用行波进位加法器即可）
$t_{\text{FA}}$ ：全加器的延迟（关键路径有 $k$ 个全加器，就是位数最高的块的行波进位加法器里面的；其他块都可以提前结束计算，对总延迟没有影响）

当 $N > 16$ 时，CLA会比行波进位加法器快很多。然而，加法器的延迟仍然随 $N$ 的增长而线性增长。

图示：
先行进位加法器

3. 前缀加法器（Prefix Adder）

策略：
- 回顾 $S_i$ 的表达式： $S_i=(A_i\oplus B_i)\oplus C_{i-1}$
- 定义第 $- 1$ 列以包含 $C_{\text{in}}$ ，则 $G_{-1}=C_{\text{in}}$ （ $C_{\text{in}}=1$ 就是有进位）， $P_{-1}=0$ （不可能有传播进位）
- 若从 $- 1$ 到 $i - 1$ 位中生成一个进位，则第 $i - 1$ 位会有进位输出，故 $C_{i-1}=G_{i-1:-1}$
- 生成的位要么在第 $i - 1$ 位生成，要么从之前的位中生成并传播到第 $i - 1$ 位
- 因此 $S_i=(A_i\oplus B_i)\oplus G_{i-1:-1}$

核心问题：快速计算 $G_{-1:-1},G_{0:-1},G_{2:-1},\cdots,G_{N-2:-1}$
前缀： $G_{-1:-1},G_{0:-1},G_{2:-1},\cdots,G_{N-2:-1}$ 和 $P_{-1:-1},P_{0:-1},P_{2:-1},\cdots,P_{N-2:-1}$
思想：二分法（与线段树类似）
计算 $G$ 、 $P$ 的方法：

$G_{i:j}=G_{i:k}+P_{i:k}G_{k-1:j}$
$P_{i:j}=P_{i:k}P_{k-1:j}$

证明：
(1) 根据我们前面提到的“连锁反应”，第 $j - 1$ 位的进位传播到第 $i$ 位需要 $P_j$ 到 $P_i$ 均为 $1$ ，故 $P_{i:j}=P_{i:k}P_{k-1:j}$ 。
(2) 在第 $j$ 到第 $i$ 位产生进位的条件是第 $i$ 位本身能产生进位，或第 $j$ 到 $i - 1$ 位能传播进位且第 $i$ 位能传播进位。所以我们有递推公式 $G_{i:j}=G_i+P_iG_{i-1:j}$ 。同理，条件也可以是第 $j + 1$ 到第 $i$ 位能产生进位，或第 $j$ 位能产生进位且第 $j + 1$ 到第 $i$ 位能传播进位，所以有 $G_{i:j}=G_{i:j+1}+P_{i:j+1}G_j$ 。
下面采用数学归纳法证明 $G_{i:j}=G_{i:k}+P_{i:k}G_{k-1:j}$ 。
①当 $k = i$ 时，注意到 $G_{i:k}=G_{i:i}=G_i$ ， $P_{i:k}=P_{i:i}=P_i$ ，故结论显然成立。
②假设当 $k = u$ 时成立。则当 $k = u - 1$ 时， $G_{i:j}=G_{i:u}+P_{i:u}G_{u-1:j}=G_{i:u}+P_{i:u}(G_{u-1}+P_{u-1}G_{u-2:j})=(G_{i:u}+P_{i:u}G_{u-1})+P_{i:u}P_{u-1}G_{u-2:j}=G_{i:u-1}+P_{i:u-1}G_{u-2:j}=G_{i:k}+P_{i:k}G_{k-1:j}$ ，结论成立。
综上，计算 $G$ 、 $P$ 的方法是正确的。