前提基础

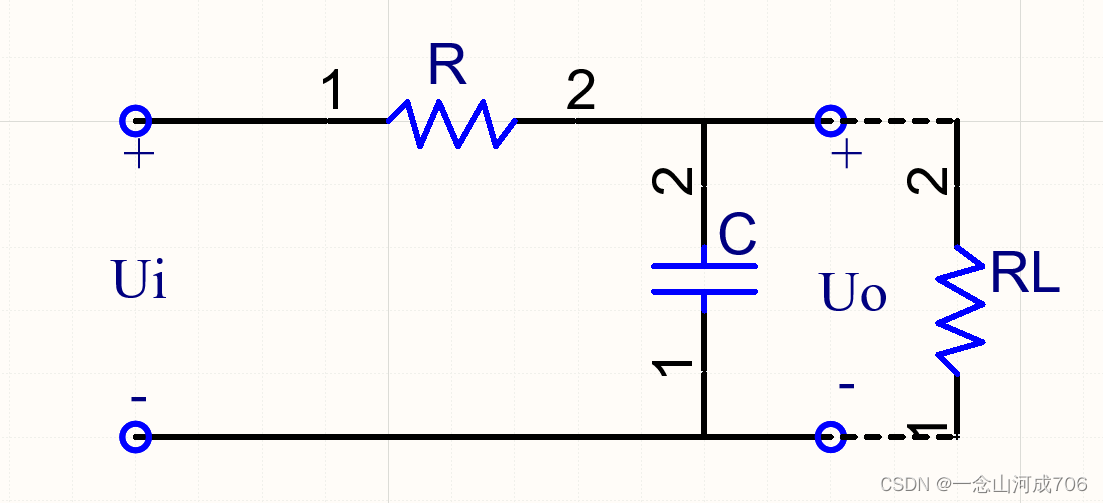
   总所周知，滤波器分为有源滤波器和无源滤波器，两者区别在于是否需要提供额外的电源。其中无源滤波器又分为RC滤波器和LC滤波器两种，最简单的RC低通滤波器如下图所示。

   由于负载电阻的存在，在空载和存在负载时滤波器的截止频率和通带放大倍数均会发生变化，具体变化如下：
空载：
$$A_{up}=1f_p=\frac{1}{2\pi RC}$$
$$A_u=\frac{1}{1+j\frac{f}{f_p}}$$
带载:
$$A_{up}=\frac{R_L}{R+R_L}$$
$$f_p=\frac{1}{2\pi (R//R_L)C}$$
   可见RC滤波器会有一定的损耗，另外的LC滤波器在此不再详细描述。

有源巴特沃斯滤波器结构

二阶和三阶有源滤波器

   有源巴特沃斯滤波器的基础结构是RC滤波器，但是用运放去消除了负载带来的截止频率变化和损耗。运放可以接成同向和反向两种放大电路，此处只考虑同向接法，基础结构为一个运放组成的二阶和三阶节，如下图所示（单倍增益）

令电路中所有电阻为1，通过电路分析中的电流环路定理和电压环路定理来计算传输函数得：
$$T(S{)}_2=\frac{1}{C_1{C}_2{S}^2+2C_{2}S+1}$$
$$T(S{)}_3=\frac{1}{C_1{C}_2{C}_3{S}^3+2C_2(C_1+C_2)S^2+(C_2+3C_3)S+1}$$
上面三阶节传输函数存疑，推测可能是下式，具体可能需要利用电路分析知识进行分析：
$$T(S{)}_3=\frac{1}{C_1{C}_2{C}_3{S}^3+2C_3(C_1+C_2)S^2+(C_2+3C_3)S+1}$$
这两个传递函数直接从电路中得来，在设计巴特沃斯滤波器时，其2阶和3阶的归一化传递函数为:
$$T(S{)}_2=\frac{1}{S^2+\sqrt{2}S+1}$$
$$T(S{)}_3=\frac{1}{S^3+2S^2+2S+1}$$
通过比较系数，对于二阶的有：
$$\begin{array}{rl}& C_1{C}_2=1\\ & 2C_2=\sqrt{2}\end{array}$$
对于三阶的有：
$$\begin{array}{rl}& C_1{C}_2{C}_3=1\\ & 2C_2(C_1+C_2)=2\\ & C_2+3C_3=2\end{array}$$
三阶校正后为：
$$\begin{array}{rl}& C_1{C}_2{C}_3=1\\ & 2C_3(C_1+C_2)=2\\ & C_2+3C_3=2\end{array}$$
解方程组可以得到：
对于二阶：
$$\begin{array}{rl}& C_1=\sqrt{2}=1.414\\ & 2C_2=\frac{1}{\sqrt{2}}=0.7071\end{array}$$
对于三阶：
$$C_1=3.546,C_2=1.392,C_3=0.2024$$
   需要注意的是，此方程由归一化传递函数解出，所以算出的电容值也是归一化的值，单位为F，电路中R均为1欧姆，也是归一化的值，在设计实际参数时必须去归一化，在后面实际设计中给出去归一化方法。

高阶有源滤波器

   4阶以上的有源滤波器可以用前面给出的2阶和三阶有源滤波器进行组合，根据系统传递函数之间的关系，最终系统传递函数应为组合的各个滤波器的乘积，即：
$$H(S)=H_1(S)H_2(S)H_3(S)\dots H_n(S)$$
下面给出4阶到7阶滤波器的级联配置：

1. 4阶（=2+2）
   

2. 5阶（=3+2）
   

3. 6阶（=2+2+2)
   

4. 7阶（=3+2+2）
   

此处直接给出归一化低通巴特沃斯滤波器分母多项式：

此图来自链接: 巴特沃斯滤波器设计

括号内即为每一级的2阶节或3阶节有源滤波器传输函数。

同时直接给出解归一化后各元件参数值：

解归一化

   解法1：令R=1ohm，再将所有电抗元件（L，C）都除上一个频率标度系数FSF，就可以把一个已知滤波器响应指标标定到不同的频率范围，即解归一化。FSF=要求频率/现在参考频率，如现在参考频率为${\omega }_c=1rad/s$，而要求参考频率为$2\pi f_c$($f_c$是实际题目中要求频率。

   解法2：解法 1 中算得的元件实际值很不实际，电容值太大，电感值太小，R=1om 更是不现实。这是必须用阻抗标度 Z 来解决。任何线性有源或无源网络，如果所有电阻和电感值乘以 Z，而所有电容除以同样的系数 Z，其传递函数不变。原因是传递函数中的 Z 抵消之故。此处不对此进行证明。采用解法2进行去归一化，去归一化数值由下式给出：
$$\begin{array}{rl}& R^{{}^{\prime }}=R\times Z\\ & L^{{}^{\prime }}=\frac{L\times Z}{FSF}\\ & C^{{}^{\prime }}=\frac{C}{FSF\times Z}\end{array}$$

设计举例

要求：
   有源低通滤波器；
   在75Hz处衰减3dB;
   在150Hz处最小衰减30dB;
   增益为1；

设计步骤：
   （1）根据陡度系数来确定滤波器阶数：因为$A_S=150/75=2$，即要求滤波器在2rad/s处最小衰减30dB。从巴特沃斯滤波器幅频响应图如下可看出：

   5阶巴特沃斯滤波器满足需求。
   （2）确定电路形式，根据有无增益要求选择合适电路。
   （3）获取R、C归一化值，根据前面给出的归一化低通巴特沃斯滤波器分母多项式与巴特沃斯滤波器2阶节或3阶节形式对比获得R、C，前面已经给出方法。
   （4）解归一化;先确定阻抗标度系数Z， 根据滤波器所处频段选择，低频段Z取大一点，否则反之。本题截止频率低至75Hz，Z取大一点，取$Z=R=50Kohm，FSF=2\pi \times f_c=471.2$，于是可得实际C值：
   3阶节点：
$$\begin{array}{rl}& C_1^{{}^{\prime }}=\frac{C_1}{FSF\times Z}=\frac{1.753}{471.2\times 5\times 10^4}=0.074uF\\ & C_2^{{}^{\prime }}=0.057uF{C}_3^{{}^{\prime }}=0.018uF\end{array}$$
   2阶节点：
$$C_1^{{}^{\prime }}=0.137uF{C}_2^{{}^{\prime }}=0.013uF$$
   (5)元件值代入归一化电路得到最后使用的滤波器电路如下;

后记

   其余类型的有源滤波器可以根据其不同阶数的传输函数用相同的方法进行设计。