动态规划-多边形游戏算法
动态规划-多边形游戏全网最详解
动态规划-多边形游戏算法
一、多边形游戏简介
首先,多边形游戏是一个单人玩的游戏。
游戏初始时是由n(n>=3)个顶点构成的多边形,每个顶点被赋予一个整数值,每条边被赋予一个运算符“+”或“×”(只有这两种),所有边依次用整数从1到n编号。
第一步:选择一条边删除(原本的多边形变成一条由数值和符号组成的链);
第二步:选择一条边,以及该边连接的两个顶点V1和V2;
第三步:用一个新的顶点替代上述边和顶点,新顶点的值为V1,V2经过中间的运算符运算后得到的结果;
第四步:重复迭代第二步和第三步,直至所有的边都被删除,只剩下一个结点,得到最终结果。
胜利条件: 对于给定的多边形,计算出最终结点的值最大。
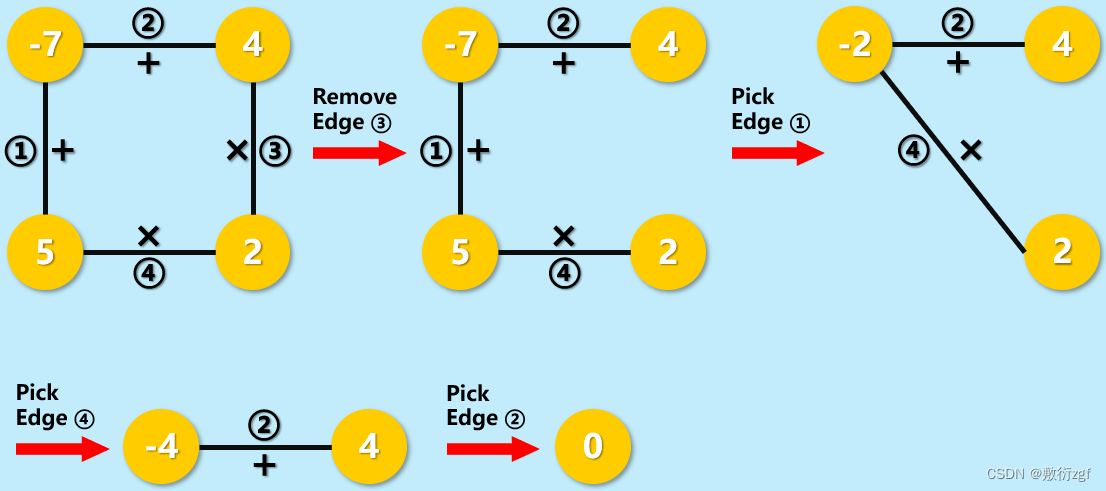
二、多边形游戏实例图

三、最优子结构性质
首先说说什么是最优子结构:我们在设计动态规划算法的第一步通常是要刻画最优解的结构。当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。例如在矩阵连乘积最优计算次序问题中,若A1A2…An的最优完全加括号方式在Ak和A(k+1)之间(1<k< n),将矩阵链断开,则由此确定子链A1A2…Ak和A(k+1)A(k+2)…An的完全加括号方式也最优,即该问题具有最优子结构性质。
我们在解决动态规划相关的问题时,可以利用问题的最优子结构性质,以自底向上的方式递归的从子问题的最优解逐步构造出整个问题的最优解。
说了这么多,我想能大概理解什么是最优子结构了,那么在解决多边形游戏的问题中,也需要用到最优子结构的性质,只不过它的最优子结构性质更具有 一般性。
(一)将图形用数学符号表示
设所给的多边形的顶点和边的顺时针序列为op[1],v[1],op[2],v[2],…,op[n],v[n].
其中op[i]表示第i条边所相对应的运算符(+ 或者 ×),v[i]表示第i个顶点上的数值(i=1~n)
在所给多边形中,从顶点i(1<=i<=n)开始,长度为j(链中有j个顶点)的顺时针链p(i,j)
可表示为:v[i],op[i],…,v[i+j-1].
如果这条链的最后一次合并运算在op[i+s-1]处发生(1<=s<=j-1),
则可在op[i+s-1]处将链分割成两个子链p(i,s) 和 p(i+s,j-s)
文字描述太抽象,来看看图吧

从顶点i开始,顺时针选取长度为j个顶点形成链p(i,j)
可表示为:v[i],op[i],…,v[i+j-2],op[i+j-2],v[i+j-1]. 从图中可以看出,由于是从多边形当中选取的j个结点,因此是一条链而不是一个封闭图形.

若这条链的最后一次合并运算在op[i+s-1]处发生,则可在op[i+s-1]处将链分割成两个子链p(i,s) 和 p(i+s,j-s)

(二)找子链的最大值与最小值
设m1是对子链p(i,s)的任何一种合并方式得到的值,而a和b分别是在所有可能的合并中得到的最小值和最大值。m2是对子链p(i+s,j-s)的任何一种合并方式得到的值,而c和d分别是在所有可能的合并中得到的最小值和最大值,则有 a<=m1<=b,c<=m2<=d
由于子链p(i,s)和子链p(i+s,j-s)的合并方式决定了p(i,j)在op[i+s-1]处断开后的合并方式,在op[i+s-1]处合并后其值为 m = (m1) op[i+s-1] (m2) ,其中 op[i+s-1]是运算符,将 m1和m2通过运算符计算的到最终结果m. 那么接下来就将 op[i+s-1] 分成两种情况(× 和 +)进行分析
(1) 若 op[i+s-1] = ’ + ’ ,则有 a+c <= m < = b+d ,其中a+c 是两个子链的最小值;b+d是两个子链的最大值。
(2) 若op[i+s-1] = ’ * ',则有min{ac,ad,bc,bd} <= m <= max{ac,ad,bc,bd}
这里需要注意的是v[i]可能取负数,子链的最大值相乘未必能得到主链的最大值,但是主链的最大值和最小值可以由子链的最大最小值得到。
那么通过上述证明,我们可以得到一个很重要的结论:
整个链的最大值和最小值可以通过子链的最大值和最小值求解得出,也就是说其具有最优子结构的性质。
四、递归求解
设m[i,j,0]、m[i,j,1]分别是链p(i,j)合并的最小值和最大值,其中i表示子链的起始位置,j表示子链长度(包含顶点个数);
如果这条链的最优合并运算在op[i+s-1]处发生(1<=s<=j),将p(i,j)分成了两个长度小于j的子链p(i,s) 和 p(i+s,j-s),那么可以记 a=m[i,s-1,0],b=m[i,s-1,1],c=m[i+s,j-s,0],d=[i+s,j-s,1]
(1) 当 op[i+s-1]= ‘+’ 时,m[i,j,0] = a+c ,m[i,j,1] = b+d
(2) 当 op[i+s-1]= ’ * ’ 时,m[i,j,0] = min{ac,ad,bc,bd} ,m[i,j,1] = max{ac,ad,bc,bd}
综上,我们已经将p(i,s) 在 op[i+s]处断开的最大值与最小值表示出来了,为了方便找出规律,我们再将其用分段函数表示,其中 最小值为min f(i,j,s),最大值为max f(i,j,s)。


由于最优的断开位置有s种(1<= s <= j-1),共j-1种情况,那么


初始边界为 :
m[i,1,0] = v[i] ,1 <= i <= n
m[i,1,1] = v[i] ,1 <= i <= n
由于多变形是封闭的,在上面的计算中,当i+s-1>n时,顶点i+s实际编号为 (i+s-1) mod n ,按上述递推式计算出的m[i,n,1]记为游戏首次删除第i条边后得到的最大得分。
五、算法实现
# 主函数
# 自定义creatVE()函数,创建多边形的顶点和边
vertexs,edges = creatVE() # vertexs顶点集合 edges边的集合
if vertexs == 0:
print("输入的顶点数和边数不一致!")
else:
n = len(vertexs)
# 自定义creatArray()函数,创建一个n*n*2的三维列表
arr = creatArray(n,vertexs)
# 自定义assigement方法,完成三维列表赋值操作
arr= assigement(arr,n) # 在arr三维列表中
max_zo = arr[0][n-1][1] # 拿到存放在arr[0][n-1][1]的数值, 默认在最大值
min_zo = arr[0][n-1][0] # 拿到存放在arr[0][n-1][0]的数值, 默认在最小值
max_index = 0
for i in range(1,n):
if max_zo < arr[i][n-1][1]: # 依次将三位列表中的arr[i][n-1][1]数值与默认的max_zo进行比较
max_zo = arr[i][n-1][1] # 哪个大,就将其赋给max_zo,使得max_zo中始终保存的是最大值
max_index = i # 保存最大值对应的索引,目的是能够输出运算过程
print("合并后的最大值为:{}".format(max_zo))
# 输出路径
print("合并的运算为:" + flashBack(arr,vertexs,edges,max_index,n-1,max_zo))
# 自定义creatVE()函数,创建多边形的顶点和边
def creatVE():
n = input("请输入顶点和边的个数:")
# 利用map函数将字符串列表转换为整数列表,相比于for循环来说,map函数节省内存,运行更快,实现简单
vertexs = list(map(int,input("顶点分别为(用空格分隔):").split()))
edges = list(input("每条边上的运算为(+或*,用空格分隔):").split())
# 对输入的数据进行校验,例如 输入的边数和顶点数不相等,或者输入边的个数和n不等,那么返回0
if len(vertexs) == len(edges) and len(vertexs) == int(n):
return vertexs,edges
else:
return 0,0
# 利用for循环实现字符串列表转换成整数列表
# list_of_strings = ["5","6","7","8","9", "10"]
# result = []
# for string in list_of_strings:
# result.append(int(string))
# print(result)
# 自定义creatArray()函数 创建一个n*n*2的三维列表
def creatArray(n,vertexs) :
'''
创建并初始化一个n*n*2的三维列表
arr[i][j][k]:第i个数据开始长度为j的链条的最值(k=1最大值;k=0最小值)
arr[i][0][k]初始化为第i个元素的值
'''
# 初始化空列表
arr = []
for i in range(n):
row = [] # 初始化 n个空列表
for j in range(n):
if j == 0 : # 每一个列表的第一列初始化值为vertexs[i]
row.append([vertexs[i], vertexs[i]])
else : # 每一个列表的剩余部分,初始化为 -inf 和 inf
row.append([-float("inf"), float("inf")]) # 用float("inf")表示正无穷 -float("inf") 表示负无穷
# print(row)
arr.append(row)
return arr
# 自定义assigement()方法,完成三维列表赋值操作 版本一
def assigement(arr,n):
# arr:列表 n:顶点个数 返回值 arr
for j in range(1,n): # j 表示长度 1~n-1
for i in range(n): # i 表示初始顶点 0 ~ n-1
minNum = float("inf")
maxNum = -float("inf")
# s : 表示长度,对长度为j的链表,在i+s-1处断开 将其分成长s 和 j-s的两段,得出最大和最小的分割情况以及最值
for s in range(1,j+1): # for循环中,j最大取n-1 故这里s 最大取到j 也就是n-1 1<=s<=j
if edges[(i+s-1)%n] == "+" : # 之所以对n取余是因为当i+s-1>n时,顶点i+s-1实际编号为 (i+s-1) mod n
minNum = min(minNum,arr[i][s-1][0] + arr[(i+s)% n][j-s][0]) # min() 取最小值 a = arr[i][s-1][0] c = arr[(i+s)% n][j-s][0]
maxNum = max(maxNum,arr[i][s-1][1] + arr[(i+s)% n][j-s][1]) # max() 取最大值 b = arr[i][s-1][1] d = arr[(i+s)% n][j-s][1]
else : # *乘法
minNum = min(minNum,min(arr[i][s-1][0] * arr[(i+s)%n][j-s][0],arr[i][s-1][0]*arr[(i+s)%n][j-s][1],arr[i][s-1][1]*arr[(i+s)%n][j-s][0],arr[i][s-1][1]*arr[(i+s)%n][j-s][1]))
maxNum = max(maxNum,max(arr[i][s-1][0] * arr[(i+s)%n][j-s][0],arr[i][s-1][0]*arr[(i+s)%n][j-s][1],arr[i][s-1][1]*arr[(i+s)%n][j-s][0],arr[i][s-1][1]*arr[(i+s)%n][j-s][1]))
arr[i][j][0] = minNum # 存放最小值
arr[i][j][1] = maxNum # 存放最大值
print(arr)
return arr
# 自定义flashBack()函数 输出路径
def flashBack(arr,vertexs,edges,i,j,num):
# i:第i次某个边断开;j:长度
n = len(vertexs)
if j == 0: #长度为0,直接输出
return str(vertexs[i]) # 返回结点的值
for s in range(j):
if edges[(i+s)%n]=="+":
if arr[i][s][1] + arr[(i+s+1) % n][j - s - 1][1] == num: # 若子部分相加为最大值 递归
return "("+flashBack(arr,vertexs,edges,i,s,arr[i][s][1])+"+"+flashBack(arr,vertexs,edges,(i+s+1)%n,j-s-1,arr[(i+s+1)%n][j-s-1][1])+")"
elif arr[i][s][0] + arr[(i + s +1) % n][j - s][0] == num:
return "("+flashBack(arr,vertexs,edges,i,s,arr[i][s][0])+"+"+flashBack(arr,vertexs,edges,(i+s+1)%n,j-s-1,arr[(i+s+1)%n][j-s-1][0])+")"
else:
# list列表中存放ac,ad ,bc,bd 交叉相乘的结果
list = [arr[i][s][0]*arr[(i+s+1)%n][j-s-1][0],arr[i][s][0]*arr[(i+s+1)%n][j-s-1][1],arr[i][s][1]*arr[(i+s+1)%n][j-s-1][0],arr[i][s][1]*arr[(i+s+1)%n][j-s-1][1]]
if num in list:
index = list.index(num)
if index == 0: # ac的结果
return "("+flashBack(arr,vertexs,edges,i,s,arr[i][s][0])+"*"+flashBack(arr,vertexs,edges,(i+s+1)%n,j-s-1,arr[(i+s+1)%n][j-s-1][0])+")"
elif index == 1: # ad的结果
return "("+flashBack(arr,vertexs,edges,i,s,arr[i][s][0])+"*"+flashBack(arr,vertexs,edges,(i+s+1)%n,j-s-1,arr[(i+s+1)%n][j-s-1][1])+")"
elif index == 2: # bc的结果
return "("+flashBack(arr,vertexs,edges,i,s,arr[i][s][1])+"*"+flashBack(arr,vertexs,edges,(i+s+1)%n,j-s-1,arr[(i+s+1)%n][j-s-1][0])+")"
else: # bd的结果
return "("+flashBack(arr,vertexs,edges,i,s,arr[i][s][1])+"*"+flashBack(arr,vertexs,edges,(i+s+1)%n,j-s-1,arr[(i+s+1)%n][j-s-1][1])+")"


开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容





所有评论(0)