一、前置知识

文字（literal）：布尔变量变量或其否定称为文字。例如，对于变量$p$，$p$和$\neg p$都是文字。（其实我也不知道怎么翻译literal qwq）

子句（clause）/简单析取式：仅由有限个文字构成的析取式称为子句或简单析取式。例如对于变量$p,q,r,s$，$\neg p\vee q\vee \neg r\vee s$就是一个简单析取式。

合取范式（Conjunctive Normal Form, CNF）：仅由有限个简单析取式构成的合取式称为合取范式。例如对于变量$p,q,r,s$，$(p\vee \neg q)\wedge (\neg p\vee r\vee s)\wedge \neg r\wedge (s\vee \neg s)$就是一个合取范式。这里为方便起见，可以将合取范式记为集合的形式，例如该范式就可记为 { { p , ¬ q } , { ¬ p , r , s } , { ¬ r } , { s , ¬ s } } \{\{p,\neg q\},\{\neg p,r,s\},\{\neg r\},\{s,\neg s\}\} {{p,¬q},{¬p,r,s},{¬r},{s,¬s}}。

CDCL（Conflict Driven Clause Learning）的目标就是判断一个合取范式是不是可满足的。显然，一个合取范式是可满足的，当且仅当它的每一个子句都是可满足的。而要满足一个子句，只需要使该子句中的某一个文字取真即可。

目前，CDCL是求解这个问题最高效的算法之一。

二、单位传播（Unit Propagation）

单位传播（Unit Propagation, UP）或布尔约束传播（Boolean Constraint Propagation, BCP）或单一文字规则（One-Literal Rule, OLR）是一个能够简化合取范式的方法。

定义单位子句（unit clause）为只有一个文字的子句，例如$p$和$\neg q$。因为它是在一个合取范式里面的，那么要满足该合取范式，这个单位子句必须为真；而单位子句又只有一个文字，所以这个文字也必须为真。如果一个合取范式包含一个单位子句$l$，那么该CNF中的其他子句就可以被$l$化简。具体做法如下：

1. 如果某个子句中含有$l$，那么就把这个子句移除。

   例如，单位子句$l=a$，CNF为$(a\vee \neg b\vee c)\wedge a\wedge (\neg d\vee e)$，可以看出该CNF有一个子句是单位子句$l$，那么要满足该CNF，就必须满足$a$，即$a=1$必须成立；而$a=1$了，那么子句$a\vee \neg b\vee c$也肯定为真，所以该子句可在CNF中可以被剔除。

   也可以用等值演算的方式理解：$(a\vee \neg b\vee c)\wedge a⟺(a\vee (\neg b\vee c))\wedge a⟺a$（使用了吸收率）。

2. 如果某个子句中含有$\neg l$，那就在这个子句中把$\neg l$移除。

   例如，单位子句$l=\neg a$，其否定$\neg l=a$；CNF为$\neg a\wedge (a\vee b\vee \neg c)\wedge (d\vee \neg e\vee f)$，可以看出该CNF有一个子句是单位子句$l$，另一个子句$a\vee b\vee \neg c$中含有$\neg l=a$。要满足该CNF，$l$必须为真，$a$必须为假；既然$a$为假，$a\vee b\vee \neg c$就是$0\vee b\vee c$，也就是$b\vee c$，因此可以把$a$也就是$\neg l$去掉。

   用等值演算的方式理解：$\neg a\wedge (a\vee b\vee \neg c)⟺(\neg a\wedge a)\vee (\neg a\wedge (b\vee \neg c))⟺0\vee (\neg a\wedge (b\vee \neg c))⟺\neg a\wedge (b\vee \neg c)$。

一个综合的例子：设CNF为$(a\vee b)\wedge (\neg a\vee c)\wedge (\neg c\vee d)\wedge a$，那么用$a$把前两个子句处理得到$c\wedge (\neg c\vee d)\wedge a$。此时还可以用$c$继续处理，得到$c\wedge d\wedge a$。

当然，实际应用中会出现单位子句的情况是很少的。不过，我们仍然可以创造条件来应用单位传播方法。对于一个含有多个文字的子句，我们可以令其中一个文字为真，其他文字均为假，就可以把它变成一个单位子句。例如对于CNF：$(a\vee \neg b\vee c)\wedge (\neg b\vee \neg c\vee d)$，令$a=0,b=1$，则由于第一个子句为真，要求$c$必须为真。此时就可以应用单位传播方法，将第二个子句化为$\neg b\vee d$。

再令$a=0,c=0$，则必有$b=0$，此时可以把第二个子句直接剔除。

也可以用等值演算理解：$$\begin{array}{rl}(a\vee \neg b\vee c)\wedge (\neg b\vee \neg c\vee d)& ⟺(a\wedge \neg b)\vee (a\wedge \neg c)\vee (a\wedge \neg d)\vee (\neg b\wedge \neg b)\vee (\neg b\wedge \neg c)\vee (\neg b\wedge \neg d)\vee (c\wedge \neg b)\vee (c\wedge \neg c)\vee (c\wedge \neg d)\\ & ⟺(a\wedge \neg b)\vee (a\wedge \neg c)\vee (a\wedge \neg d)\vee \neg b\vee (\neg b\wedge \neg c)\vee (\neg b\wedge \neg d)\vee (c\wedge \neg b)\vee (c\wedge \neg d)\\ & ⟺(a\wedge \neg b)\vee (a\wedge \neg c)\vee (a\wedge \neg d)\vee \neg b\vee (c\wedge \neg d)\end{array}$$其中，$a=0,b=1,c=1$对应式中的$c\wedge \neg d$项，$a=0,c=0,b=0$对应式中的$\neg b$项。

有时对某个单位子句应用单位传播可能会导致另一个子句成为单位子句（例如我们上面举的综合例子），因此算法会不断地应用单位传播方法，直到化到最简为止。

三、DPLL（Davis-Putnam-Logemann-Loveland）算法

要讲CDCL，就不得不提到DPLL，因为CDCL是DPLL的进化版。

DPLL是一种基于回溯的算法，它的核心步骤就是单位传播（CDCL也是一样）。一个朴素的回溯算法可能会尝试每种可能的赋值，直到找到一组成真赋值为止。而DPLL可以利用单位传播来进行“更聪明”的猜测，从而减小搜索树的大小（可以将单位传播看成一种剪枝策略）。

在求解的过程中，如果我们发现某个子句的真值为真，就删除这个子句；如果发现某个文字的真值为假，就在子句中删除这个变量。这样，最后发现CNF为空，就说明所有子句都满足了，即该CNF是可满足的；如果发现CNF中有一个子句为空而该子句没有被删除，说明这个子句的所有文字取值都为假，于是这个子句不能满足，此次赋值尝试是失败的。

我们先看一下朴素算法的伪代码：

朴素算法(CNF):
    找到CNF中下一个没有被赋值的变量;
    if 找到了:
        return 朴素算法(CNF中这个变量为真) || 朴素算法(CNF中这个变量为假);
    else: // 没找到，说明所有变量均已赋值
        return CNF在该组赋值下的真值;

再看一下DPLL的伪代码：

DPLL(CNF):
    while CNF含有单位子句:
        对该CNF使用单位传播;
    if CNF为空:
        return true;
    else if CNF有空子句:
        return false;
    else: // 仍不能确定CNF的值，需要对更多的变量赋值
        找到CNF中下一个没有被赋值的变量（或文字）;
        return DPLL(CNF中这个变量为真) || DPLL(CNF中这个变量为假);

可以在Conflict Driven Clause Learning (cse442-17f.github.io)看一个交互式的例子，对理解这个算法很有帮助。

下面给出DPLL的Python代码，使用sympy库：

from sympy import Symbol
from sympy.logic.boolalg import Not
from typing import *
from copy import deepcopy

Literal = Union[Symbol, Not]

class ConjunctiveNormalForm: # 合取范式类
    def __init__(self, l: List[Set[Literal]]):
        # l: 集合的列表，里面的集合是子句，外面的列表是CNF
        self.cnf = l
        self.preprocess()
    def preprocess(self):
        for clause in list(self.cnf):
            for literal in clause:
                if ~literal in clause:
                    self.cnf.remove(clause) # x | ~x等价于1，删除该子句
                    break
    def find_unit_clause(self): # 找到单位子句
        for clause in self.cnf:
            if len(clause) == 1:
                return list(clause)[0] # 返回单位子句含有的文字
        return None # 找不到，返回None
    def unit_propagation(self, literal: Literal):
        # 以文字literal对cnf进行单位传播
        for clause in list(self.cnf): # 需要拷贝self.cnf
            if literal in clause: # 含有literal的子句直接删除
                self.cnf.remove(clause)
        for clause in self.cnf:
            if ~literal in clause:
                clause.remove(~literal) # 删除literal的否定
    def evaluate(self): # 对CNF求值
        if len(self.cnf) == 0: # CNF为空，可满足
            return True
        elif set() in self.cnf: # CNF含有空子句，不满足（出现矛盾）
            return False
        return None # 无法确定，返回None
    def find_next_unevaluated_literal(self): # 找到下一个没有被赋值的文字
        return list(self.cnf[0])[0] # 直接返回第一个子句的第一个文字

def DPLL(c: ConjunctiveNormalForm):
    literal = None
    while True: # 不断使用单位传播，直到没有单位子句为止
        literal = c.find_unit_clause() # 找到单位子句包含的文字
        if literal == None: # 无单位子句，退出循环
            break
        c.unit_propagation(literal) # 执行单位传播
    v = c.evaluate() # 求值
    if v == True:
        return True
    elif v == False:
        return False
    else: # 仍不能确定CNF的值，向下递归
        literal = c.find_next_unevaluated_literal()
        # 找到下一个没有被赋值的文字
        c1 = ConjunctiveNormalForm(deepcopy(c.cnf))
        c1.unit_propagation(literal) # 让这个文字取真
        if DPLL(c1):
            return True
        c2 = ConjunctiveNormalForm(deepcopy(c.cnf))
        c2.unit_propagation(~literal) # 让这个文字取假
        if DPLL(c2):
            return True
        return False

示例：对合取范式$(\neg c)\wedge (\neg b)\wedge (d\vee e)\wedge (\neg a)\wedge (a\vee c)$进行DPLL：

from sympy import symbols
a, b, c, d, e = symbols('a b c d e')
l = [{~c}, {~b}, {d, e}, {~a}, {a, c}]
print(DPLL(ConjunctiveNormalForm(l))) # 输出False

DPLL是一个很简单的算法，不过就是朴素算法加上单位传播而已（当然也可以采用其他改进策略进一步优化，比如采用“纯文字”（pure literal）法等）。它的最坏复杂度仍然是指数级别的。

四、CDCL（Conflict-Driven Clause Learning）算法

Conflict-Driven Clause Learning，直译过来是“冲突驱动的子句学习”，也就是从冲突中吸取教训，做出更合理的猜测。所谓冲突，就是出现某个子句的所有文字都为false，使得该子句不可能被满足。出现这种情况时，我们可以从中总结出关于文字取值的一些限制，根据这些限制进行决策，进而提升算法效率。CDCL相比于DPLL最大的特点是“non-chronological back-jumping”，即“非时序性回溯”，换言之就是回溯时不一定回到上一层，而可能回到上几层。

从冲突中吸取教训的过程称为子句学习。当冲突发生时，我们分析冲突发生的原因，学习一个新的子句并加入CNF中，该子句可以使得这个冲突被避免，并且其他类似的冲突也可能被避免。完成子句学习后，我们进行回溯，回溯到哪一层取决于刚才分析的结果。

下面给出CDCL的伪代码。因为使用递归不容易实现回溯到上面几层的过程，所有我们使用非递归写法，并引入“决策层”（Decision Level）的概念。

CDCL(CNF):
    副本 = CNF // 创建CNF的副本，不更改原CNF
    while true:
        while 副本含有单位子句:
            对副本使用单位传播;
        if 副本中含有取值为假的子句: // 发现冲突
            if 现在的决策层是0:
                return false; // 不能满足
            C = 子句学习(CNF, 副本) // 吸取教训
            根据C回到一个更早的决策层; // 调整策略
        else:
            if 所有变量都被赋值:
                return true; // 可满足
            else: // 进行一次决策（决策就是一次尝试，令某个文字为真，撞大运）
                开始一个新的决策层;
                找到一个未赋值的文字l;
                副本 = 副本∧{l}
                // 给l赋值为真
                // 加入l构成的单位子句，使得副本要满足就是l要满足，变相地要求l为真
                // 对于变量x，若给x赋值为真，就令l = x；若给x赋值为假，就令l = ¬x

那么下面我们就细致地实现这个算法。

1. 迹（Trail）与决策层

要分析冲突出现的原因，我们需要记得在当前采用的赋值下为什么某个文字会取一个特定的值，这样才能不断地调整策略。这个实现记忆功能的结构就是迹。迹是一串连在一起的文字，里面出现的每个文字代表这个文字赋值为真；同时我们要记录为什么这个文字赋值为真，于是在文字的右上角标注原因。当文字是因为一次决策取真时，我们就标“决策”；当文字因为副本中的某个子句而被迫取真时，我们就标注这个子句。例如：$$x_1^{\text{决策}}\cdot x_2^{(\neg x_1\vee x_2)}\cdot \neg x_3^{(\neg x_1\vee \neg x_3)}\cdot \neg x_4^{(\neg x_1\vee \neg x_2\vee \neg x_4)}$$代表如下含义：首先$x_1$在一次决策中被赋值为真；CNF中有子句$\neg x_1\vee x_2$，要满足这个子句，因为$\neg x_1$为假，所以$x_2$必为真；又根据子句$\neg x_1\vee \neg x_3$，可知$\neg x_3$必为真，即$x_3$必为假；而在子句$\neg x_1\vee \neg x_2\vee \neg x_4$中，$\neg x_1$和$\neg x_2$都为假，那么$\neg x_4$只能取真。

如何动态地维护迹呢？我们采用如下规则：

• 如果算法做出决策使文字$l$为真，那么在迹的末尾添加$l^{\text{决策}}$；
• 如果算法在子句 C = { l 1 ∨ l 2 ∨ ⋯ ∨ l k ∨ l } C=\{l_1\lor l_2\lor\cdots\lor l_k\lor l\} C={l1​∨l2​∨⋯∨lk​∨l}上实施单位传播，而$l_1,l_2,\cdots ,l_k$都赋值为假，这使得$l$只能取真，那么就在迹的末尾添加$l^C$；
• 如果算法回溯了，那么某些元素将被从迹的末尾被移除。

这样，现在的赋值就可以从迹中清楚地看出来。我们定义迹中一个文字的决策层是迹中该文字前面（包含它自己）决策文字（即右上角标注为“决策”）的个数。换言之，决策层就是目前有多少个变量是由决策而赋值的。例如，在迹$x_1^{\text{决策}}\cdot \neg x_2^{(\neg x_1\vee \neg x_2)}\cdot x_3^{\text{决策}}\cdot x_4^{(\neg x_1\vee \neg x_3\vee x_4)}$中，$x_1$、$x_2$的决策层是$1$，$x_3$、$x_4$的决策层是$2$。

2. 蕴含图（Implication Graph）、子句学习和回溯

前面介绍的迹是一个线性结构，但如果我们把推导的关系也考虑进来，那么我们将会看到它变成一个有向无环图。事实上，算法不会真的去构建这样一张图，而是会直接使用迹来进行运算。

考虑CNF为$$\begin{array}{r}(\neg x_1\vee \neg x_2)\wedge (\neg x_1\vee x_3)\wedge (\neg x_3\vee \neg x_4)\wedge (x_2\vee x_4\vee x_5)\wedge (\neg x_5\vee x_6\vee \neg x_7)\wedge (x_2\vee x_7\vee x_8)\wedge (\neg x_8\vee \neg x_9)\\ \wedge (\neg x_8\vee x_{10})\wedge (x_9\vee \neg x_{10}\vee x_{11})\wedge (\neg x_{10}\vee \neg x_{12})\wedge (\neg x_{11}\vee x_{12})\end{array}$$首先我们决定令$x_1$为真，那么经过单位传播后得出迹为$x_1^{\text{决策}}\cdot \neg x_2^{(\neg x_1\vee \neg x_2)}\cdot x_3^{(\neg x_1\vee x_3)}\cdot \neg x_4^{(\neg x_3\vee \neg x_4)}\cdot x_5^{(x_2\vee x_4\vee x_5)}$。我们可以总结出变量之间的蕴含关系：

• 已知$x_1$为真，根据子句$(\neg x_1\vee \neg x_2)$有$\neg x_2$，故$x_1\models \neg x_2$；
• 已知$x_1$为真，根据子句$(\neg x_1\vee x_3)$有$x_3$，故$x_1\models x_3$；
• 已知$x_3$为真，根据子句$(\neg x_3\vee \neg x_4)$有$\neg x_4$，故$x_3\models \neg x_4$；
• 已知$x_2$为假、$x_4$为假，根据子句$(x_2\vee x_4\vee x_5)$有$x_5$，故$\neg x_2,\neg x_4\models x_5$。

由此，我们可以把变量之间的蕴含关系画成一张图：

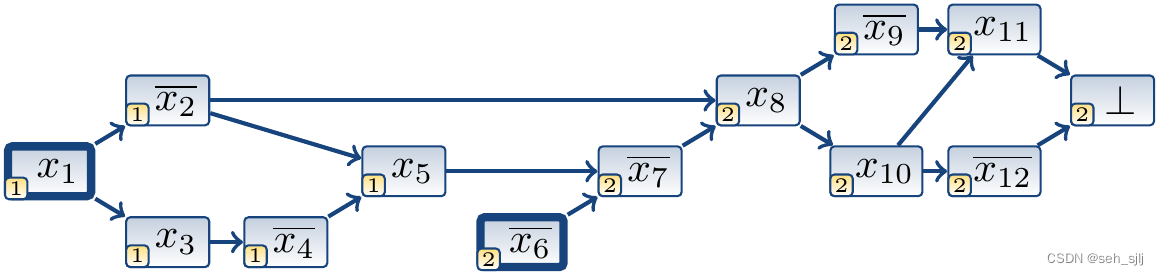
其中$\overline{x_2}$表示$\neg x_2$，左下角的数字是决策层。要继续运算，就必须再做出一次决策，决定$x_6$的值。我们决定$x_6$为假（此时开启了新的决策层），那么迹就变成了：$$\begin{array}{r}{x}_1^{\text{决策}}\cdot \neg x_2^{(\neg x_1\vee \neg x_2)}\cdot x_3^{(\neg x_1\vee x_3)}\cdot \neg x_4^{(\neg x_3\vee \neg x_4)}\cdot x_5^{(x_2\vee x_4\vee x_5)}\cdot \\ \neg x_6^{\text{决策}}\cdot \neg x_7^{(\neg x_5\vee x_6\vee \neg x_7)}\cdot x_8^{(x_2\vee x_7\vee x_8)}\cdot \neg x_9^{(\neg x_8\vee \neg x_9)}\cdot x_{10}^{(\neg x_8\vee x_{10})}\cdot x_{11}^{(x_9\vee \neg x_{10}\vee x_{11})}\cdot \neg x_{12}^{(\neg x_{10}\vee \neg x_{12})}\end{array}$$对应的蕴含图如下：

CNF中还有一个子句$(\neg x_{11}\vee x_{12})$，但$x_{11}$为真、$x_{12}$为假，所以这个子句不能被满足，也就是说我们发现了矛盾，用$\perp$表示。该$\perp$节点的入边是由造成冲突的子句$(\neg x_{11}\vee x_{12})$产生的。

现在我们在数学上给出蕴含图的定义：

设有迹$\pi$。一个对应的蕴含图$G_{\pi }$是一个有向无环图$(V,E)$，其中点集 V = { l ∣ l r ∈ π } V=\left\{l|l^r\in\pi\right\} V={l∣lr∈π}（也就是$\pi$中出现的文字集）。边集$E$的构造方式如下：对于CNF中的每个子句$C=(l_1\vee l_2\vee \cdots \vee l_k\vee l)$，若$l^C\in \pi$，则$E$含有边$(\neg l_i,l)$，$1\le i\le k$。此外，如果$\pi$的赋值使得子句$C=(l_1\vee l_2\vee \cdots \vee l_k)$不可满足，则$V$还含有一个特殊的冲突节点$\perp$，$E$还含有边$(\neg l_i,\perp )$，$1\le i\le k$。

显然，蕴含图是有向无环图，且决策文字的节点（包含$x_j^{决策}$的节点）入度为$0$（上图中的$x_1$和$\overline{x_6}$）。迹就是蕴含图的一个拓扑序。

有了蕴含图，我们就可以分析冲突出现的原因。在上例中，为什么子句$(\neg x_{11}\vee x_{12})$不能满足呢？因为$x_{11}$为真且$x_{12}$为假。为什么$x_{11}$为真且$x_{12}$为假呢？因为$x_9$为假且$x_{10}$为真。为什么$x_9$为假且$x_{10}$为真呢？因为$x_8$为真。为什么$x_8$为真呢？因为$x_2$为假且$x_7$为假。……依此类推，最终推出原因是$x_1$为真且$\neg x_6$为假。为了吸取教训、不让冲突再次发生，我们可以在CNF中加入一个子句来约束决策的过程。比如可以加入$(x_9\vee \neg x_{10})$、$\neg x_8$、$(\neg x_1\vee x_6)$等。有了这个子句约束，下次决策时就不会得到相同的冲突了。这个用于约束的子句就是我们学习到的子句。

要对学到的子句进行数学上的描述，就需要用到点割集的概念。设蕴含图$G_{\pi }=(V,E)$，它的一个冲突切割（conflict cut）就是点集$V$的一个分割$W=(A,B)$，使得：

• 所有决策文字的节点属于$A$；
• 冲突节点属于$B$；
• $A\cap B=\varnothing$；
• $A\cup B=V$。

令 R = { l ∈ A ∣ ∃ l ′ ∈ B , ( l , l ′ ) ∈ E } R=\{l\in A|\exists l'\in B,(l,l')\in E\} R={l∈A∣∃l′∈B,(l,l′)∈E}称为该冲突切割的原因集（reason set），它包含的是$A$中有连到$B$的边的节点的集合，它是$G_{\pi }$的一个点割集。

那么，该冲突切割对应的学到的子句就是$\underset{l\in R}{\bigvee }\neg l$。

接下来，我们对刚才的例子考察冲突切割：

• 在下面的切割中， A = { x 1 , ¬ x 6 } A=\{x_1,\neg x_6\} A={x1​,¬x6​}， R = { x 1 , ¬ x 6 } R=\{x_1,\neg x_6\} R={x1​,¬x6​}，学到的子句是$\neg x_1\vee x_6$。

  

• 在下面的切割中， A = { x 1 , ¬ x 2 , x 3 , ¬ x 4 , x 5 , ¬ x 6 } A=\{x_1,\neg x_2,x_3,\neg x_4,x_5,\neg x_6\} A={x1​,¬x2​,x3​,¬x4​,x5​,¬x6​}， R = { ¬ x 2 , x 5 , ¬ x 6 } R=\{\neg x_2,x_5,\neg x_6\} R={¬x2​,x5​,¬x6​}，学到的子句是$x_2\vee \neg x_5\vee x_6$。

  

• 在下面的切割中， A = { x 1 , ¬ x 2 , x 3 , ¬ x 4 , x 5 , ¬ x 6 , ¬ x 7 , x 8 } A=\{x_1,\neg x_2,x_3,\neg x_4,x_5,\neg x_6,\neg x_7,x_8\} A={x1​,¬x2​,x3​,¬x4​,x5​,¬x6​,¬x7​,x8​}， R = { x 8 } R=\{x_8\} R={x8​}，学到的子句是$\neg x_8$。

  

• A = { x 1 , ¬ x 2 , x 3 , ¬ x 4 , x 5 , ¬ x 6 , x 10 } A=\{x_1,\neg x_2,x_3,\neg x_4,x_5,\neg x_6,x_{10}\} A={x1​,¬x2​,x3​,¬x4​,x5​,¬x6​,x10​}， R = { ¬ x 2 , x 5 , ¬ x 6 , x 10 } R=\{\neg x_2,x_5,\neg x_6,x_{10}\} R={¬x2​,x5​,¬x6​,x10​}，学到的子句是$x_2\vee \neg x_5\vee x_6\vee \neg x_{10}$。
  

冲突切割有很多，那到底选哪一个进行学习呢？实践中，我们只关心具有某些特性的冲突切割。我们希望学到的子句最好能引发新的单位传播过程。

唯一蕴含点（unique implication point, UIP）：如果蕴含图$G_{\pi }$中的某个节点$l$是唯一蕴含点，那么设$d$是最近一次做决策的节点（即包含决策层最深的决策文字的节点），$d$到冲突节点的所有路径都必须经过$l$。例如上图中$d=\overline{x_6}$，冲突节点为$\perp$，$l$可以是$\overline{x_6}$，$\overline{x_7}$或$x_8$。

如果$l$是一个唯一蕴含点，那么对应的唯一蕴含冲突切割（UIP cut）是$(A,B)$，其中$B$包含了所有是$l$的后继、并且有到冲突节点的路径的节点。$A$则包含了剩下的节点。

注意：唯一蕴含冲突切割的原因集并不一定只包含唯一蕴含点。

注意到唯一蕴含点是必然存在的，因为最近一次做决策的节点就是唯一蕴含点。特别地，我们使用第一个唯一蕴含冲突切割（first UIP cut）：使集合$A$尽可能大的唯一蕴含冲突切割（这是为了减少回溯的层数，充分利用前面的计算结果）。

再次考察下面的蕴含图。它的最近一次做决策的节点是$\overline{x_6}$，因为它的决策层最深，是$2$。它有三个蕴含点：$\overline{x_6},\overline{x_7},x_8$。

• 下图所示的冲突切割不是唯一蕴含冲突切割，因为集合$B$含有除唯一蕴含点$\overline{x_6}$的后继以外的节点$x_1$。
  

• 下图是唯一蕴含冲突切割，但不是第一个唯一蕴含冲突切割。
  

• 下图也是唯一蕴含冲突切割，但也不是第一个唯一蕴含冲突切割。
  

• 下图就是第一个唯一蕴含冲突切割。

  

假设我们从唯一蕴含冲突切割中学到的子句是$C$，那么$C$其实是CNF的一个逻辑上的结果，不满足$C$就不满足CNF。

经过学习之后，CDCL算法现在进行非时序性回溯：

• 令$m$是$C$的文字中第二深的决策层（如果$C$中的文字全部都是一个决策层，则$m=0$）；
• 从迹中删除所有决策层大于$m$的文字。

这样的回溯策略可以撤销最近一次决策，并在上一个决策层应用我们学到的子句进而运行单位传播，以此来更快地决定某些变量的值。

论断 $C$中有且仅有一个文字属于最近的一个决策层。

证明：设$C$是由唯一蕴含冲突切割$(A,B)$中学到的，我们令该切割中的唯一蕴含点为$l$，那么从最近一次决策的点$d$到冲突节点$\perp$的所有路径都经过$l$。显然$l$属于原因集$R$，因此$l$在$C$中出现。若有另一个节点$u$也在$C$中出现且$u$和$d$在一个决策层，那么$u$是$d$的后继，而且$u\in R$。于是$\exists u^{\prime }\in B$使得$(u,u^{\prime })\in E$。设所有从$d$出发经过$u$和$u^{\prime }$到$\perp$的路径集合为$P$，我们证明一定存在$p\in P$使得$p$不经过$l$。

首先，若$p=d\to u\to u^{\prime }\to \perp$经过$l$，那么$l$一定不在$u\to u^{\prime }$和$u^{\prime }\to \perp$段，因为$l\in A$。于是$l$只能在$d\to u$上出现。那么所有从$d$到$u$的路径都经过$l$吗？如果是这样，则$u$是$l$的后继，而$u$又有到$\perp$的路径，因此根据唯一蕴含冲突切割的定义，应有$u\in B$，这与$u\in R\subseteq A$矛盾。因此这样的$u$不存在，论断得证。

推论 若$C$中的文字全部都是一个决策层，则$C$只含有一个文字。

在$C$只含有一个文字$l$的情况下，$l$取真是冲突发生的全部原因；换言之，只要$l$取真，那么冲突一定会发生，与前面做了什么决策无关。因此$\neg l$是CNF的直接推论，它应该在决策层为$0$时就得到应用。此时我们回溯到$m=0$层。

还是考察上面的例子。唯一蕴含点为$x_8$，$C=\neg x_8$，得到这个子句后算法回到第$0$层并以$\neg x_8$进行单位传播。最后得到的迹为$\neg x_8^{(\neg x_8)}$。

再给出一个回溯到第一层的例子。如果我们采用下图所示的唯一蕴含冲突切割：

$C=x_2\vee \neg x_5\vee x_6$，$m=1$，在迹中删除决策层大于$1$的文字后应用$C$进行单位传播，得到的新迹是$x_1^{\text{决策}}\cdot \neg x_2^{(\neg x_1\vee \neg x_2)}\cdot x_3^{(\neg x_1\vee x_3)}\cdot \neg x_4^{(\neg x_3\vee \neg x_4)}\cdot x_5^{(x_2\vee x_4\vee x_5)}\cdot x_6^{(x_2\vee \neg x_5\vee x_6)}$。

总的来说，

• 对于可满足的CNF，CDCL算法最终找到一个成真赋值，赋值方式存储在迹中。
• 对于不可满足的CNF，CDCL算法最终会返回“不可满足”（false）。这是因为每次冲突都会产生一个新的子句，而只存在有限个可能的子句，因此在某一时刻算法会产生足够多的单位子句，进而在决策层$0$产生一个冲突，这表示CNF是不可满足的。或者也可以这样理解：在学到的子句的约束下，同一组赋值一定不会出现第二次，而赋值可能的组数是有限的，所以算法一定会在有限步内停止。

下面给出一个CDCL在一个例子上的具体工作流程：

设CNF为$(a\vee b\vee c)\wedge (a\vee b\vee \neg c)\wedge (\neg b\vee d)\wedge (a\vee \neg b\vee \neg d)\wedge (\neg a\vee e\vee f)\wedge (\neg a\vee e\vee \neg f)\wedge (\neg e\vee \neg f)\wedge (\neg a\vee \neg e\vee f)$。那么CDCL可以按照如下的步骤运作：

1. 该CNF不含单位子句，因此在决策层$0$我们不做任何事。

2. 在决策层$1$，我们做出一次决策：令$a$为假。单位传播不做任何事，因此迹为$\neg a^{\text{决策}}$。

3. 在决策层$2$，我们再做一次决策：令$b$为假。对子句$(a\vee b\vee c)$进行单位传播，得到$c$为真，因此迹为$\neg a^{\text{决策}}\cdot \neg b^{\text{决策}}\cdot c^{(a\vee b\vee c)}$。此时我们发现：子句$(a\vee b\vee \neg c)$为假，我们得到了一个冲突。
   

   最近一次做决策的节点是$\overline{b}$，它同时也是唯一蕴含点。 A = { a ‾ , b ‾ } A=\{\overline a,\overline b\} A={a,b}， B = { c , ⊥ } B=\{c,\perp\} B={c,⊥}，原因集 R = { a ‾ , b ‾ } R=\{\overline a,\overline b\} R={a,b}，学习到的子句$C=(a\vee b)$。其中$\overline{a}$的决策层是$1$，$\overline{b}$的决策层是$2$，因此$m=1$，回到决策层$1$。

4. 在决策层$1$，首先利用学到的子句$(a\vee b)$进行单位传播，推出$b$为真，然后根据$(\neg b\vee d)$推出$d$为真。现在的迹是$\neg a^{\text{决策}}\cdot b^{(a\vee b)}\cdot d^{(\neg b\vee d)}$。然而，我们又发现了冲突：子句$(a\vee \neg b\vee \neg d)$不能满足。
   

   最近一次做决策的节点是$\overline{a}$，它同时也是唯一蕴含点。 A = { a ‾ } A=\{\overline a\} A={a}， B = { b , d , ⊥ } B=\{b,d,\perp\} B={b,d,⊥}，原因集 R = { a ‾ } R=\{\overline a\} R={a}，学到的子句$C=(a)$，仅含有一个文字，故算法回溯到第$0$层。

5. 在决策层$0$，利用学到的子句$(a)$进行单位传播，没有推测出其它变量的值。现在的迹是$a^{(a)}$。

6. 在决策层$1$，我们做出一次决策：令$e$为假。进行单位传播：根据子句$(\neg a\vee e\vee f)$，得知$f$为真。现在的迹是$a^{(a)}\cdot \neg e^{\text{决策}}\cdot f^{(\neg a\vee e\vee f)}$。此时我们发现子句$(\neg a\vee e\vee \neg f)$不能满足。

   

   最近一次做决策的节点是$\overline{e}$，它同时也是唯一蕴含点。 A = { a , e ‾ } A=\{a,\overline e\} A={a,e}， B = { f , ⊥ } B=\{f,\perp\} B={f,⊥}，原因集 R = { a , e ‾ } R=\{a,\overline e\} R={a,e}，学到的子句$C=(\neg a\vee e)$，其中$a$在第$0$层，$\overline{e}$在第$1$层，$m=1$，回溯到第$0$层。

7. 在决策层$0$，利用子句$(a)$进行对学到的子句$C=(\neg a\vee e)$单位传播，得到$(e)$。再进行单位传播，根据子句$(\neg e\vee \neg f)$知道$f$为假，此时迹为$a^{(a)}\cdot e^{(\neg a\vee e)}\cdot \neg f^{(\neg e\vee \neg f)}$。而CNF中的最后一个子句是$(\neg a\vee \neg e\vee f)$，得不到满足，所以我们在决策层$0$发现了矛盾，这意味着该CNF是不可满足的。

CDCL还有很多优化策略，比如采用启发式决策（Decision Heuristics）、利用数据结构加速单位传播过程、在遇到困难时重启等，这里就不再赘述了。

下面给出一个CDCL的Python实现：

from sympy import Symbol
from sympy.logic.boolalg import Not
from typing import *
from copy import deepcopy

Literal = Union[Symbol, Not]

class Clause: # 子句类
    def __init__(self, c: Set[Literal], i: int):
        self.clause = c
        self.index = i # 该子句是CNF的第几个子句
        self.value = None # 目前该子句的赋值
    def __repr__(self):
        return f'[Clause {self.clause} index={self.index} ' + \
            f'value={self.value}]'
    def __eq__(self, o):
        if hasattr(o, 'clause'):
            return self.clause == o.clause
        else:
            return False

class CDCLSolver: # 基于CDCL算法的合取范式可满足性问题求解器
    class Trail: # 迹类
        class DecisionLevel: # 按决策层分开
            class Node: # 节点类
                def __init__(self, lit: Union[Literal, None], dl: int,
                    rs: Union[Clause, None]):
                    self.literal = lit # 文字
                    self.dl = dl # 决策层
                    self.reason = rs # 赋值原因（None=决策）
                def __repr__(self):
                    return f'<({self.dl}) {self.literal} {self.reason}>'
                def __eq__(self, o):
                    return self.literal == o.literal and self.dl == o.dl \
                        and self.reason == o.reason
                def __hash__(self):
                    return hash((self.literal, self.dl))
            def __init__(self, dl: int):
                self.dl = dl
                self.nodes = [] # List[Node]
            def __repr__(self):
                return str(self.nodes)
        def __init__(self):
            self.levels = [self.DecisionLevel(0)]
        def append_level(self, dl: int):
            self.levels.append(self.DecisionLevel(dl))
        def append_node_to_current_level(self,
            lit: Literal, rs: Union[Clause, None]):
            self.levels[-1].nodes.append(self.DecisionLevel.Node(
                lit, self.levels[-1].dl, rs))
        def __repr__(self):
            return str(self.levels)

    def __init__(self, l: List[Set[Literal]]):
        # CDCLSolver的构造函数
        self.cnf = []
        i = 0
        for clause in l:
            self.cnf.append(Clause(clause, i))
            i += 1
        self.trail = self.Trail() # 迹
        self.assignments = dict() # 当前赋值
        for clause in l:
            for literal in clause:
                if literal not in self.assignments and \
                    ~literal not in self.assignments:
                    self.assignments[literal] = None
        # 所有变量赋值均为None，即未赋值
    def get_value(self, l: Literal) -> Union[bool, None]:
        # 获取文字l的赋值
        if l in self.assignments:
            return self.assignments[l]
        if ~l in self.assignments:
            r = self.assignments[~l]
            if r == None:
                return None
            else:
                return not r
    def set_value(self, l: Literal):
        # 设置文字l的赋值为True，或者设置~l的赋值为False
        if l in self.assignments:
            self.assignments[l] = True
        if ~l in self.assignments:
            self.assignments[~l] = False
    def clear_value(self, l: Literal):
        # 让文字l回到未赋值的状态
        if l in self.assignments:
            self.assignments[l] = None
        if ~l in self.assignments:
            self.assignments[~l] = None
    def find_unit_clause(self) -> \
        Union[Tuple[Literal, Clause], Tuple[None, None]]:
        # 寻找单位子句，返回对应的文字，找不到返回None
        for clause in self.cnf:
            len_clause = len(clause.clause) # 子句文字个数
            num_undefined = 0 # 子句中未赋值的文字个数
            num_false = 0 # 子句中取值为假的文字个数
            undefined_literal = None # 未赋值的文字
            for literal in clause.clause:
                value = self.get_value(literal)
                if value == False:
                    num_false += 1
                elif value == None:
                    undefined_literal = literal
                    num_undefined += 1
            if num_undefined == 1 and num_false == len_clause - 1:
                return undefined_literal, clause
        return None, None
    def update_clause_value(self): # 更新子句的值
        for clause in self.cnf:
            len_clause = len(clause.clause)
            num_true = 0 # 取真的文字的个数
            num_false = 0 # 取假的文字的个数
            for literal in clause.clause:
                r = self.get_value(literal)
                if r == True:
                    num_true += 1
                elif r == False:
                    num_false += 1
            if num_true >= 1: # 至少有一个文字取真
                clause.value = True # 则子句取真
            elif num_false == len_clause: # 所有文字取假（冲突）
                clause.value = False # 则子句取假
            else: # 还不能确定子句的取值（没有文字取真，但并不都取假）
                clause.value = None # 待定
    def propagate_literal(self, literal: Literal,
        clause: Union[Clause, None]):
        # 传播文字literal的赋值
        self.set_value(literal) # 设置literal的赋值为真
        self.update_clause_value() # 更新子句的值
        self.trail.append_node_to_current_level(literal, clause)
        # 在迹中添加节点
    def unit_propagation(self): # 单位传播
        # 动态维护变量赋值、子句赋值和迹
        literal = None # 用于单位传播的文字
        while True:
            literal, clause = self.find_unit_clause()
            if literal == None:
                break # 不能进行单位传播了
            self.propagate_literal(literal, clause)
    def detect_conflict(self) -> Union[Clause, None]: # 检查是否有冲突
        for clause in self.cnf:
            if clause.value == False: # 若发现取值为假的子句，返回该子句
                return clause
        return None
    def find_unassigned_literal(self) -> Union[Literal, None]:
        # 找到一个未赋值的文字，找不到就返回None
        for literal, value in self.assignments.items():
            if value == None: # 若某子句的取值为None，说明它未赋值
                return literal
        return None

    def clause_learning(self, conflict_clause: Clause) -> \
            Tuple[Clause, int]: # 子句学习
        latest_level_nodes = self.trail.levels[-1].nodes
        # 最近一次决策层的节点
        can_be_UIP = dict()
        # 存储每个最近一层的节点是否可能是唯一蕴含点的字典
        for node in latest_level_nodes:
            can_be_UIP[node] = True # can_be_UIP先全部设置为True
        # 由于迹是蕴含图的拓扑序，如果某条最近一层节点之间的边跨过了某个节点，
        # 那么这个节点必然不是唯一蕴含点（有路径不经过该节点）
        # 下面按正向建图
        conflict_node = self.Trail.DecisionLevel.Node(None,
            self.trail.levels[-1].dl, conflict_clause) # 冲突节点
        all_nodes = latest_level_nodes + [conflict_node]
        # 所有最近一层的节点，包括冲突节点
        V = set() # 计算顶点集V
        for level in self.trail.levels:
            for node in level.nodes:
                V.add(node)
        V.add(conflict_node)
        adjacency_list = dict() # 最近一层的邻接表
        for node in all_nodes:
            adjacency_list[node] = []
        node_from_literal = dict() # 从文字到节点的字典
        for node in V:
            node_from_literal[node.literal] = node
        all_literals = set() # all_nodes对应的文字集合
        for node in all_nodes:
            all_literals.add(node.literal)
        for node in all_nodes: # 构造邻接表
            rs = node.reason
            if rs != None:
                for from_literal in rs.clause:
                    if from_literal != node.literal \
                        and ~from_literal in all_literals:
                        from_node = node_from_literal[~from_literal]
                        adjacency_list[from_node].append(node)
        # 下面按边排除不可能是唯一蕴含点的节点
        i = iter(all_nodes)
        for node in latest_level_nodes:
            next(i)
            for to in adjacency_list[node]:
                j = deepcopy(i)
                while True:
                    k = next(j)
                    if k == to:
                        break
                    can_be_UIP[k] = False
        UIP = None # 唯一蕴含点
        for node in reversed(latest_level_nodes):
        # 寻找唯一蕴含点
        # 节点的拓扑序越靠后，说明以它作为唯一蕴含点，唯一蕴含冲突切割的A集合越大
        # 因此拓扑序最靠后的唯一蕴含点就是对应于第一个唯一蕴含冲突切割的唯一蕴含点
            if can_be_UIP[node]:
                UIP = node
                break
        can_reach_conflict_node = set() # 可到达冲突节点的节点
        Q = [conflict_node] # 利用广度优先搜索进行计算，Q是队列
        while len(Q) > 0:
            u = Q[0]
            can_reach_conflict_node.add(u)
            del Q[0]
            rs = u.reason
            if rs != None:
                for literal in rs.clause:
                    if literal != u.literal and \
                        ~literal in all_literals:
                        node = node_from_literal[~literal]
                        Q.append(node)
        successor_of_UIP = set() # 唯一蕴含点的所有后继
        Q = [UIP] # 仍然广度优先搜索进行计算
        while len(Q) > 0:
            u = Q[0]
            del Q[0]
            for node in adjacency_list[u]:
                successor_of_UIP.add(node)
                Q.append(node)
        B = can_reach_conflict_node.intersection(successor_of_UIP)
        # B包含是UIP的后继并且能到达冲突节点的节点，所以取两个集合的交集
        A = V - B # 冲突切割W=(A,B)，A∪B=V
        R = set() # 原因集
        entire_adjacency_list = dict() # 整个蕴含图的邻接表
        for node in V:
            entire_adjacency_list[node] = []
        for node in V: # 构造entire_adjacency_list
            rs = node.reason
            if rs != None:
                for from_literal in rs.clause:
                    if from_literal != node.literal:
                        from_node = node_from_literal[~from_literal]
                        entire_adjacency_list[from_node].append(node)
        for node in A: # 找出R中的元素
            for to in entire_adjacency_list[node]:
                if to in B:
                    R.add(node)
                    break
        new_clause = set()
        for node in R:
            new_clause.add(~node.literal)
        learned_clause = Clause(new_clause, len(self.cnf)) # 学到的子句
        self.cnf.append(learned_clause)
        R_levels = sorted(list(set([node.dl for node in R])))
        # R的元素的决策层集合
        backtrack_level = 0
        if len(R_levels) > 1:
            backtrack_level = R_levels[-2] # 第二大
        return learned_clause, backtrack_level
        # 返回学到的子句和应回溯到的决策层
    def backtrack(self, clause: Clause, level: int): # 回溯到第level层
        while self.trail.levels[-1].dl > level: # 考察在第level层之后的层
            for node in self.trail.levels[-1].nodes:
                self.clear_value(node.literal) # 文字重新退回到未赋值状态
            self.trail.levels.pop() # 从迹中删除该层
        self.update_clause_value() # 更新子句的值

    def CDCL(self) -> bool:
        decision_level = 0 # 一开始决策层是0
        while True:
            self.unit_propagation() # 单位传播
            conflict_clause = self.detect_conflict()
            if conflict_clause != None: # 发现冲突
                if decision_level == 0:
                    return False # 在决策层0发现冲突说明不可满足
                else:
                    learned_clause, backtrack_level = \
                        self.clause_learning(conflict_clause) # 子句学习
                    self.backtrack(learned_clause,
                        backtrack_level) # 回溯
                    decision_level = backtrack_level
            else:
                literal = self.find_unassigned_literal()
                if literal == None:
                    # 所有变量均被赋值且未发生冲突，说明可满足
                    return True
                else:
                    decision_level += 1 # 开始一个新的决策层
                    self.trail.append_level(decision_level)
                    self.propagate_literal(literal, None)

参考文献

1. Unit propagation - Wikipedia
2. Conflict-driven clause learning - Wikipedia
3. Conflict Driven Clause Learning (cse442-17f.github.io)
4. CDCL SAT Solvers & SAT-Based Problem Solving (aalto.fi)
5. Conflict-driven clause learning (CDCL) SAT solvers — CS-E3220: Propositional satisfiability and SAT solvers documentation (aalto.fi)