上一篇介绍了DID，本文介绍和DID可一起搭配使用的一种因果推断方法PSM。在正式介绍PSM之前，先来简单回顾一下为什么需要因果推断以及如何做因果推断。我们都知道相关非因果，比起相关我们更希望知道两个事件之间的因果关系，有了确切的因果关系，才能知道对A如何操作才能引起B的变化。解决因果推断问题，目前主要有两种框架，Rubin虚拟事实模型和Pearl因果图模型。站在数据分析的角度上，Rubin虚拟事实模型更容易理解，其核心思想是寻找恰当的对照组。想要知道策略干预带来的效果是多少，我们需要知道该用户在干预和未干预下的表现，但同一时间内无法观测到一个用户的两种状态，所以我们就需要借助AB实验或者构造合适对照组的方式来进行评估。除了AB实验外常用的方法有：双重差分、倾向得分匹配、合成控制、断点回归、双重机器学习、因果随机森林、Uplift Model等。

二、PSM原理

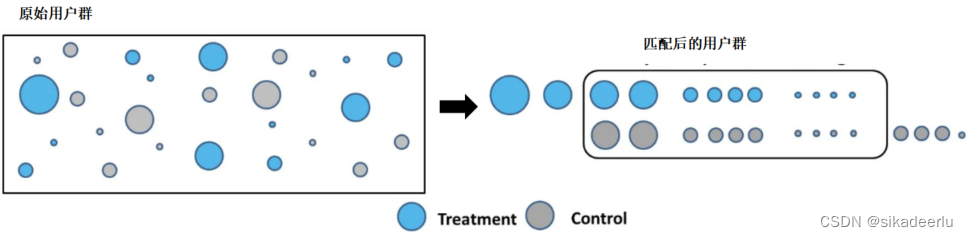
PSM的核心思想是从未受干预的用户群体中，找到和干预对象一模一样的用户，这样就可以把因果效应归因到干预上。一般来说，每个样本有多个特征，对于一个用户来说有：画像特征、行为特征等，如果每个特征都进行匹配，则维度会很多，匹配也会很困难。所以可引进倾向得分P(x)来代替，这样就可以用一维变量进行匹配，从而大大降低匹配的复杂度。

这里个体的倾向得分是指在个体情况一定的前提下，进入处理组的概率。倾向得分可用分类模型得到，选择尽可能多的协变量，类似于回归中的控制变量。计算倾向得分类似于降维的过程，把非常多的协变量维度降为一个维度，就是倾向得分。两个个体的倾向得分非常接近，并不意味着这两个个体的其他属性也接近，这不好判断。不过根据PSM的原理，倾向得分接近就够了，其他属性也接近更好。匹配后可进一步验证其他属性是否更接近了。

2.1 前提条件

（1）样本量要足够大，如果太小，很多干预组的样本可能在控制组匹配不到对象，或者能匹配但是距离很远，也就是匹配度不高。

（2）干预组与控制组的倾向得分要有较大的共同取值范围，否则会丢失较多样本，导致匹配的样本不具代表性。

2.2 实施步骤

1. 倾向得分计算：因变量为是否被干预，自变量为用户特征，建立LR/XGB/RF等模型预测用户进入干预组的概率，以该概率作为倾向得分，也可以其Logit（ ln(e(x)/1-e(x) ）作为倾向得分。

2. 倾向得分匹配：为干预组用户，在非干预组中匹配一个近似相同的用户，作为对照组

a. 修剪：去除掉倾向得分比较极端的用户，常见的做法是保留得分在[a, b]这个区间的用户。实验组和对照组得分区间的交集，只保留区间中部的90%或95%，如原始得分在[0.05, 0.95]的用户。

b. 匹配：实验组和对照组用户根据得分进行匹配。常用方法有knn和radius，knn即对实验组进行1对k有放回或无放回匹配。radius:对实验组用户，匹配所有得分差异小于radius的用户。

c. 设置得分差异上限：当我们匹配用户时，要求每一对用户的得分差异不超过指定的上限。

3. 平衡性检验：用Cohen’s d效应量衡量匹配后的实验组和对照组在各个特征上的差异，其计算公式如下：

$d = \frac{\bar{x_{t}} - \bar{x_{c}}}{s}$

$s = \frac{\sqrt{(n_{t} - 1)s_{t}^{2} + (n_{c} - 1)s_{c}^{2} }}{n_{t} + n_{c} - 2 }$

该值的分子为实验组和对照组平均值之差，分母为两组的汇总方差，一般该值不超过0.2则认为匹配通过平衡性检验。

4. 因果效应估计：我们的目标是计算策略干预组的ATT(Average Teamtment Effect on then Treated)。可用匹配到的干预组和对照组计算核心指标的提升情况，从而得到因果效应。

三、应用案例代码

3.1 自己实现psm

1. 数据读入及各特征显著性检验

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math

# 1. 引入数据
df = pd.read_csv('./data/groupon.csv')

df.head()
# 2. 查看实验组/对照组各特征的均值
df.groupby('treatment').count()
df.groupby('treatment').mean()


# 3. 实验组/对照组各特征差异显著性 
df_control = df[df.treatment==0]
df_treatment = df[df.treatment==1]

# 以 revenue 为例 
from scipy.stats import ttest_ind

# 查看两组的均值
print(df_control.revenue.mean(), df_treatment.revenue.mean()) 

# t检验
_, p = ttest_ind(df_control.revenue, df_treatment.revenue)
print(f'p={p:.3f}')

# 输出是否差异是否显著
alpha = 0.05  # 显著水平设为 0.05
if p > alpha:
    print('两者分布无差异（没有足够的证据拒绝原假设）')
else:
    print('两者分布差异显著（拒绝原假设）')

2. 建模及添加psm得分

a. 建立逻辑回归模型

# 1. 模型数据准备
X = df[['prom_length', 'price', 'discount_pct', 'coupon_duration', 'featured', 'limited_supply']]
y = df['treatment']


# 2. 建立逻辑回归模型，预测用户进入干预组的概率
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X, y)

# 查看逻辑回归模型各个特征的系数
coeffs = pd.DataFrame({
    'column':X.columns.to_numpy(),
    'coeff':lr.coef_.ravel(),
})
coeffs

b. 添加psm得分

# 3. 添加倾向匹配得分
df['ps'] = pred_prob[:, 1]

# 添加logit后的得分
def logit(p):
    logit_value = math.log(p / (1-p))
    return logit_value

df['ps_logit'] = df.ps.apply(lambda x: logit(x))

df.head()

3. 查看实验组和对照组倾向得分的重叠度

sns.histplot(data=df, x='ps', hue='treatment')

可以看到实验组和对照组的倾向得分在0.05-0.6之间有较多的重合，所以可进行匹配。

4. 用knn为实验组元素匹配样本

a. 首先为每个元素都进行knn，匹配得分范围在25%标准差内的10个最近的元素

from sklearn.neighbors import NearestNeighbors

# 1. 以ps得分标准差的25%作为半径，匹配相邻的10个元素，半径越大或者k越大，可匹配到的元素越多
n_neighbors = 10
caliper = np.std(df.ps) * 0.25
print(f'caliper (radius) is: {caliper:.4f}')

# 2. knn
knn = NearestNeighbors(n_neighbors=n_neighbors, radius=caliper)

ps = df[['ps']]  
knn.fit(ps)

# 3. 返回每个点相邻点的索引和距离
distances, neighbor_indexes = knn.kneighbors(ps)  

print(neighbor_indexes.shape)  # 输出neighbor_indexes的长度

# 查看第一个元素的匹配结果
print(distances[0])
print(neighbor_indexes[0])

b. 为实验组中的每个元素，在对照组中找到一个和它匹配的

matched_control = []  # 保存对照组中匹配到的观测对象

for current_index, row in df.iterrows():  # 遍历 dataframe中的每行记录
    if row.treatment == 0:   # 如果当前行是对照组
        df.loc[current_index, 'matched'] = np.nan  # 将匹配到的对象设置为nan
    else: 
        for idx in neighbor_indexes[current_index, :]: # 遍历实验组样本的10个相邻元素
            # 确保当前行不在10个相邻元素中，既排除自己
            # 并且确保相邻元素在对照组中
            if (current_index != idx) and (df.loc[idx].treatment == 0):
                if idx not in matched_control:  # 当前对象没有被匹配过
                    df.loc[current_index, 'matched'] = idx  # 记录当前的匹配对象
                    matched_control.append(idx)  # 并将其插入到待保存的数组中
                    break

df.head()

5. 对比匹配前后各个特征在实验组、对照组上的Cohen's d效应值、p值

from numpy import mean
from numpy import var
from math import sqrt
 
# 计算Cohen's d 的方法
def cohen_d(d1, d2):
    # 计算样本数量
    n1, n2 = len(d1), len(d2)
    # 计算样本方差
    s1, s2 = var(d1, ddof=1), var(d2, ddof=1)
    # 计算两者的组合方差
    s = sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
    # 计算均值
    u1, u2 = mean(d1), mean(d2)
    # 得到效应值
    return (u1 - u2) / s

effect_sizes = []
cols = ['prom_length', 'price', 'discount_pct', 'coupon_duration', 'featured','limited_supply']

for cl in cols:
    _, p_before = ttest_ind(df_control[cl], df_treatment[cl])
    _, p_after = ttest_ind(df_matched_control[cl], df_matched_treatment[cl])
    cohen_d_before = cohen_d(df_treatment[cl], df_control[cl])
    cohen_d_after = cohen_d(df_matched_treatment[cl], df_matched_control[cl])
    effect_sizes.append([cl,'before', cohen_d_before, p_before])
    effect_sizes.append([cl,'after', cohen_d_after, p_after])

可以看到匹配后除了 discount_pct 这个特征外，其余特征的 Cohen's d 效应值都有所下降，且p值都大于0.05，说明匹配后的这些特征的分部较为均衡，无显著差异。

用柱状图更直观的输出各特征Cohen's d 效应值的前后差异

# discount_pct and featured are not significant, all other features are more balanced after matching
fig, ax = plt.subplots(figsize=(15, 5))
sns.barplot(data=df_effect_sizes, x='effect_size', y='feature', hue='matching', orient='h')

3.2 用psmpy包来实现

1. psm模型初始化并计算psm得分

from psmpy import PsmPy
from psmpy.plotting import *

df_psmpy = pd.read_csv('./data/groupon.csv')
df_psmpy.info()

# 初始化
# exclude:  模型拟合时要忽略的字段
# indx: 唯一值
psm = PsmPy(df_psmpy, treatment='treatment', indx='deal_id', exclude = ['min_req', 'start_date', 'fb_likes', 'quantity_sold', 'revenue'])

# 计算logit得分
psm.logistic_ps(balance=True)  # balance=False 建模时是否让实验组和对照组的记录数保持平衡
psm.predicted_data  # 查看进入模型中的数据

2. 为实验组匹配元素，并画出匹配后的得分分布


# knn 1:1 匹配
psm.knn_matched(matcher='propensity_logit', replacement=False, caliper=None)

# 画出倾向得分的分布图
# x轴是倾向得分，y轴是匹配到的数量 
psm.plot_match(Title='Matching Result', Ylabel='# of obs', Xlabel= 'propensity logit', names = ['treatment', 'control'])

3. 画出匹配前后的效应值差异

# 画出各个特征在匹配前后的效应值
psm.effect_size_plot()

4. 其他属性及方法

# 输出匹配到的id
psm.matched_ids

# 输出匹配到的原始数据
psm.df_matched


# 输出匹配前后的效应值
psm.effect_size

# 单独使用
from psmpy.functions import cohenD
cohenD(df_psmpy, treatment = 'treatment', metricName = 'prom_length')