平衡小车动力学建模
两轮自平衡小车由车体和双轮两部分组成,可以看成一个移动的倒立摆,分别对车轮和车体进行力学分析,建立动力学模型,最后,通过对两者的分析给出系统的状态空间表达式。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kjiPEUVJ-1679470559950)(C:\Users\DELL\AppData\Roaming\Typora\typora-user-images\im
前言
两轮自平衡小车由车体和双轮两部分组成,可以看成一个移动的倒立摆,分别对车轮和车体进行力学分析,建立动力学模型,最后,通过对两者的分析给出系统的状态空间表达式。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pURItxa1-1679556611143)(C:\Users\DELL\AppData\Roaming\Typora\typora-user-images\image-20230322110521545.png)]](https://i-blog.csdnimg.cn/blog_migrate/daae7f40c7a60cc8cd7bd387123bcd4f.png)
车轮模型
以右轮为例进行受力分析,如图所示
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JGfjgfh3-1679556611143)(C:\Users\DELL\AppData\Roaming\Typora\typora-user-images\image-20230322110550417.png)]](https://i-blog.csdnimg.cn/blog_migrate/5526dfb50543ddab397d61093d65b1ae.png)
将车轮的运动分解为平动和转动,
由牛顿第二定律可得
m
x
R
¨
=
H
f
R
−
H
R
(
1
)
m\ddot{x_R}=H_{fR}-H_{R} {(1)}
mxR¨=HfR−HR(1)
由刚体定轴转动定律可得
I
ω
R
˙
=
T
R
−
H
f
R
r
(
2
)
I\dot{\omega_R}=T_R-H_{fR}r {(2)}
IωR˙=TR−HfRr(2)
其中,
| 物理量 | 描述 | 单位 |
|---|---|---|
| m m m | 车轮的质量 | k g kg kg |
| r r r | 车轮的半径 | m m m |
| x R x_R xR | 右轮的水平位移 | m m m |
| H f R H_{fR} HfR | 右轮受到地面的摩擦力的大小 | N N N |
| H R H_{R} HR | 右轮受到车体作用力的水平分力的大小 | N N N |
| T R T_{R} TR | 右轮电机输出的转矩的大小 | N ⋅ m N\cdot m N⋅m |
| I I I | 车轮的转动惯量 | k g ⋅ m 2 kg\cdot m^2 kg⋅m2 |
| ω R \omega_R ωR | 右轮的角速度的大小 | r a d / s rad/s rad/s |
联立 ( 1 ) ( 2 ) (1)(2) (1)(2),消去 H f R H_{fR} HfR,可得
m x R ¨ = T R − I ω R ˙ r − H R ( 3 ) m\ddot{x_R}=\frac{T_R-I\dot{\omega_R}}{r}-H_{R} {(3)} mxR¨=rTR−IωR˙−HR(3)
在车轮不打滑的情况下,车轮的移动速度的大小和转动速度的大小成比例关系,即
{
ω
R
=
x
R
˙
r
ω
R
˙
=
x
R
¨
r
(
4
)
\begin{cases} \omega_R=\frac{\dot{x_R}}{r} \\ \dot{\omega_R}=\frac{\ddot{x_R}}{r} \end{cases} {(4)}
{ωR=rxR˙ωR˙=rxR¨(4)
将方程
(
4
)
(4)
(4)代入
(
3
)
(3)
(3)中,消去
ω
R
˙
\dot{\omega_R}
ωR˙,可得
(
m
+
I
r
2
)
x
R
¨
=
T
R
r
−
H
R
(
5
)
(m+\frac{I}{r^2})\ddot{x_R}=\frac{T_R}{r}-H_{R} {(5)}
(m+r2I)xR¨=rTR−HR(5)
由于左右轮的参数相同,对左轮有类似的结果,即
(
m
+
I
r
2
)
x
L
¨
=
T
L
r
−
H
L
(
6
)
(m+\frac{I}{r^2})\ddot{x_L}=\frac{T_L}{r}-H_{L} {(6)}
(m+r2I)xL¨=rTL−HL(6)
车轮模型
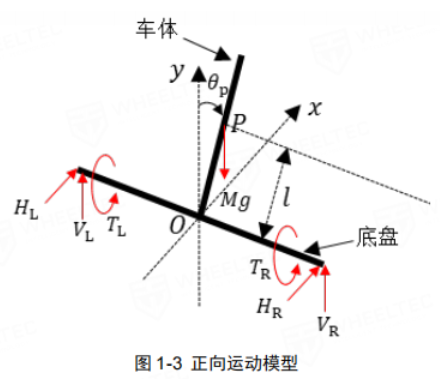
车体的运动也可以分解为正向运动(前向、俯仰)和侧向运动(转向、偏航)。
正向运动
小车的正向运动可以分解为前向运动和绕车体质心 P P P的相对转动(俯仰)。小车底盘中心 O O O的水平位移为 x = x L + x R 2 ( 7 ) x=\frac{x_L+x_R}{2} {(7)} x=2xL+xR(7)
将方程
(
5
)
(
6
)
(5)(6)
(5)(6)相加,等式两边同时除以
2
2
2可得
(
m
+
I
r
2
)
x
L
¨
+
x
R
¨
2
=
T
L
+
T
R
2
r
−
H
L
+
H
R
2
(
8
)
(m+\frac{I}{r^2})\frac{\ddot{x_L}+\ddot{x_R}}{2}=\frac{T_L+T_R}{2r}-\frac{H_{L}+H_{R}}{2}{(8)}
(m+r2I)2xL¨+xR¨=2rTL+TR−2HL+HR(8)
将
(
7
)
(7)
(7)代入
(
8
)
(8)
(8)可得
(
m
+
I
r
2
)
x
¨
=
T
L
+
T
R
2
r
−
H
L
+
H
R
2
(
9
)
(m+\frac{I}{r^2})\ddot{x}=\frac{T_L+T_R}{2r}-\frac{H_{L}+H_{R}}{2}{(9)}
(m+r2I)x¨=2rTL+TR−2HL+HR(9)

对车体,应用牛顿第二定律可得
在水平方向上,有
M
d
(
x
+
l
s
i
n
θ
P
)
d
t
2
=
H
L
+
H
R
(
10
)
M\frac{d(x+lsin\theta_P)}{dt^2}=H_L+H_R{(10)}
Mdt2d(x+lsinθP)=HL+HR(10)
在竖直方向上,有
M
d
(
l
c
o
s
θ
P
)
d
t
2
=
V
L
+
V
R
−
M
g
(
11
)
M\frac{d(lcos\theta_P)}{dt^2}=V_L+V_R-Mg{(11)}
Mdt2d(lcosθP)=VL+VR−Mg(11)
对车体,由刚体定轴转动定律可得
J
P
θ
P
¨
=
(
V
L
+
V
R
)
l
s
i
n
θ
P
−
(
H
L
+
H
R
)
l
c
o
s
θ
P
−
(
T
L
+
T
R
)
(
12
)
J_P\ddot{\theta_P}=(V_L+V_R)lsin\theta_P-(H_L+H_R)lcos\theta_P-(T_L+T_R){(12)}
JPθP¨=(VL+VR)lsinθP−(HL+HR)lcosθP−(TL+TR)(12)
其中,
| 物理量 | 描述 | 单位 |
|---|---|---|
| M M M | 车体的质量 | k g kg kg |
| l l l | 质心距底盘中心的距离 | m m m |
| J P J_P JP | 车体绕质心转动时的转动惯量 | k g ⋅ m 2 kg\cdot m^2 kg⋅m2 |
| θ P \theta_P θP | 车体与竖直方向所成的夹角 | r a d rad rad |
| V L V_L VL | 车体受到左轮作用力的竖直分力的大小 | N N N |
联立方程
(
9
)
(
10
)
(9)(10)
(9)(10),将
H
L
+
H
R
H_{L}+H_{R}
HL+HR项消去,可得
(
M
+
2
m
+
2
I
r
2
)
x
¨
−
T
L
+
T
R
r
+
M
l
θ
P
¨
c
o
s
θ
P
−
M
l
θ
P
˙
2
s
i
n
θ
P
=
0
(
13
)
(M+2m+\frac{2I}{r^2})\ddot{x}-\frac{T_L+T_R}{r}+Ml\ddot{\theta_P}cos{\theta_P}-Ml\dot{\theta_P}^2sin{\theta_P}=0(13)
(M+2m+r22I)x¨−rTL+TR+MlθP¨cosθP−MlθP˙2sinθP=0(13)
其中,
s
i
n
θ
d
t
=
θ
˙
c
o
s
θ
\frac{sin\theta}{dt}=\dot{\theta}cos\theta
dtsinθ=θ˙cosθ,
d
(
θ
˙
c
o
s
θ
)
d
t
=
θ
¨
c
o
s
θ
−
θ
˙
2
s
i
n
θ
\frac{d(\dot{\theta}cos\theta)}{dt}=\ddot{\theta}cos\theta-\dot{\theta}^2sin\theta
dtd(θ˙cosθ)=θ¨cosθ−θ˙2sinθ
方程含有非线性项,因此,进行线性化,考虑到车体的倾角比较小,通常情况下
−
1
0
∘
≤
θ
P
≤
1
0
∘
-10^{\circ}\leq\theta_P\leq10^{\circ}
−10∘≤θP≤10∘,则可以认为
{
c
o
s
θ
P
=
1
s
i
n
θ
P
=
θ
P
θ
P
˙
2
=
0
\begin{cases} cos\theta_P=1 \\ sin\theta_P=\theta_P \\ \dot{\theta_P}^2=0 \end{cases}
⎩
⎨
⎧cosθP=1sinθP=θPθP˙2=0
故方程
(
13
)
(13)
(13)变为
x
¨
=
T
L
+
T
R
(
M
+
2
m
+
2
I
r
2
)
r
−
M
l
(
M
+
2
m
+
2
I
r
2
)
θ
P
¨
(
14
)
\ddot{x}=\frac{T_L+T_R}{(M+2m+\frac{2I}{r^2})r}-\frac{Ml}{(M+2m+\frac{2I}{r^2})}\ddot{\theta_P}(14)
x¨=(M+2m+r22I)rTL+TR−(M+2m+r22I)MlθP¨(14)
将方程
(
10
)
(
11
)
(10)(11)
(10)(11)代入方程
(
12
)
(12)
(12)中,消去
H
L
+
H
R
H_L+H_R
HL+HR以及
V
L
+
V
R
V_L+V_R
VL+VR可得
(
J
P
M
l
+
l
)
θ
P
¨
+
x
¨
c
o
s
θ
P
−
g
s
i
n
θ
P
+
T
L
+
T
R
M
l
=
0
(
15
)
(\frac{J_P}{Ml}+l)\ddot{\theta_P}+\ddot{x}cos\theta_P-gsin\theta_P+\frac{T_L+T_R}{Ml}=0(15)
(MlJP+l)θP¨+x¨cosθP−gsinθP+MlTL+TR=0(15)
对方程
(
15
)
(15)
(15)进行线性化可得
θ
P
¨
=
M
l
g
(
J
P
+
M
l
2
)
θ
P
−
M
l
(
J
P
+
M
l
2
)
x
¨
−
T
L
+
T
R
(
J
P
+
M
l
2
)
(
16
)
\ddot{\theta_P}=\frac{Mlg}{(J_P+Ml^2)}\theta_P-\frac{Ml}{(J_P+Ml^2)}\ddot{x}-\frac{T_L+T_R}{(J_P+Ml^2)}(16)
θP¨=(JP+Ml2)MlgθP−(JP+Ml2)Mlx¨−(JP+Ml2)TL+TR(16)
将方程
(
16
)
(16)
(16)代入方程
(
14
)
(14)
(14)中,消去
θ
P
¨
\ddot{\theta_P}
θP¨,可得
x
¨
=
−
M
2
l
2
g
Q
e
q
θ
P
+
J
P
+
M
l
2
+
M
l
r
Q
e
q
r
(
T
L
+
T
R
)
(
17
)
\ddot{x}=-\frac{M^2l^2g}{Q_{eq}}\theta_P+\frac{J_P+Ml^2+Mlr}{Q_{eq}r}(T_L+T_R)(17)
x¨=−QeqM2l2gθP+QeqrJP+Ml2+Mlr(TL+TR)(17)
其中
Q
e
q
=
J
P
M
+
(
J
P
+
M
l
2
)
(
2
m
+
2
I
r
2
)
Q_{eq}=J_PM+(J_P+Ml^2)(2m+\frac{2I}{r^2})
Qeq=JPM+(JP+Ml2)(2m+r22I)
这里我尝试用matlab的Symbolic Math Toolbox进行符号推导:
syms M m I r
den = M + 2 * m + 2 * I / r^2
syms T_L T_R l theta_P(t) x(t)
syms x_ddot theta_P_ddot theta_P % 可以定义上下标
eqn_1 = (T_L + T_R) / (den * r) - M * l / den * theta_P_ddot == x_ddot
syms J_P g
den_2 = J_P + M * l^2
eqn_2 = theta_P_ddot == (M * l * g) / den_2 * theta_P - M * l / den_2 * x_ddot - (T_L + T_R) / den_2
% 利用subs函数进行进行代换
eqn_3 = subs(eqn_1, theta_P_ddot, (M * l * g) / den_2 * theta_P - M * l / den_2 * x_ddot - (T_L + T_R) / den_2)
% eqn_ddx = simplify(eqn_ddx) % 利用数学表达式化简
eqn_ddx = isolate(eqn_ddx, x_ddot) % 将x_ddot分离到等式一侧
latex(eqn_ddx)
% 化简为x_ddot=(a/b)theta_P_ddot+(c/d)(T_L+T_R)的形式
结果如下,和我的预期有一定差距,不知道如何通分继续化简了。
x
¨
=
−
T
L
+
T
R
r
(
M
+
2
m
+
2
I
r
2
)
+
M
l
(
T
L
+
T
R
M
l
2
+
J
P
−
M
g
l
θ
P
M
l
2
+
J
P
)
M
+
2
m
+
2
I
r
2
M
2
l
2
(
M
l
2
+
J
P
)
(
M
+
2
m
+
2
I
r
2
)
−
1
\ddot{x}=-\frac{\frac{T_{L}+T_{R}}{r\,\left(M+2\,m+\frac{2\,I}{r^2}\right)}+\frac{M\,l\,\left(\frac{T_{L}+T_{R}}{M\,l^2+J_{P}}-\frac{M\,g\,l\,\theta _{P}}{M\,l^2+J_{P}}\right)}{M+2\,m+\frac{2\,I}{r^2}}}{\frac{M^2\,l^2}{\left(M\,l^2+J_{P}\right)\,\left(M+2\,m+\frac{2\,I}{r^2}\right)}-1}
x¨=−(Ml2+JP)(M+2m+r22I)M2l2−1r(M+2m+r22I)TL+TR+M+2m+r22IMl(Ml2+JPTL+TR−Ml2+JPMglθP)
将方程
(
14
)
(14)
(14)代入方程
(
16
)
(16)
(16)中,消去
x
¨
\ddot{x}
x¨,可得
θ
P
¨
=
M
l
g
(
M
+
2
m
+
2
I
r
2
)
Q
e
q
θ
P
−
(
M
l
r
+
M
+
2
m
+
2
I
r
2
)
Q
e
q
(
T
L
+
T
R
)
(
18
)
\ddot{\theta_P}=\frac{Mlg(M+2m+\frac{2I}{r^2})}{Q_{eq}}\theta_P-\frac{(\frac{Ml}{r}+M+2m+\frac{2I}{r^2})}{Q_{eq}}(T_L+T_R)(18)
θP¨=QeqMlg(M+2m+r22I)θP−Qeq(rMl+M+2m+r22I)(TL+TR)(18)
综上所述,对于正向运动有
{
x
¨
=
−
M
2
l
2
g
Q
e
q
θ
P
+
J
P
+
M
l
2
+
M
l
r
Q
e
q
r
(
T
L
+
T
R
)
θ
P
¨
=
M
l
g
(
M
+
2
m
+
2
I
r
2
)
Q
e
q
θ
P
−
(
M
l
r
+
M
+
2
m
+
2
I
r
2
)
Q
e
q
(
T
L
+
T
R
)
(
19
)
\begin{cases} \ddot{x}=-\frac{M^2l^2g}{Q_{eq}}\theta_P+\frac{J_P+Ml^2+Mlr}{Q_{eq}r}(T_L+T_R) \\ \\ \ddot{\theta_P}=\frac{Mlg(M+2m+\frac{2I}{r^2})}{Q_{eq}}\theta_P-\frac{(\frac{Ml}{r}+M+2m+\frac{2I}{r^2})}{Q_{eq}}(T_L+T_R) \end{cases}(19)
⎩
⎨
⎧x¨=−QeqM2l2gθP+QeqrJP+Ml2+Mlr(TL+TR)θP¨=QeqMlg(M+2m+r22I)θP−Qeq(rMl+M+2m+r22I)(TL+TR)(19)
转向运动

转向运动时由左右两车轮从水平方向上施加给车体的反作用力的大小
H
L
H_L
HL和
H
R
H_R
HR不相等引起的,由刚体定轴转动定律可得
J
δ
δ
¨
=
d
2
(
H
L
+
H
R
)
(
20
)
J_{\delta}\ddot{\delta}=\frac{d}{2}(H_L+H_R)(20)
Jδδ¨=2d(HL+HR)(20)
其中,
| 物理量 | 描述 | 单位 |
|---|---|---|
| d d d | 轮距 | m m m |
| J δ J_{\delta} Jδ | 车体绕 y y y轴转动时的转动惯量 | k g ⋅ m 2 kg\cdot m^2 kg⋅m2 |
| δ \delta δ | 小车的偏航角 | r a d rad rad |
将方程
(
5
)
(
6
)
(5)(6)
(5)(6)相减得
(
m
+
I
r
2
)
(
x
L
¨
−
x
R
¨
)
=
T
L
−
T
R
r
−
(
H
L
−
H
R
)
(
21
)
(m+\frac{I}{r^2}){(\ddot{x_L}-\ddot{x_R})}=\frac{T_L-T_R}{r}-{(H_{L}-H_{R})}{(21)}
(m+r2I)(xL¨−xR¨)=rTL−TR−(HL−HR)(21)

当左右两轮运动速度不相等时,车身转向,如上图所示。由几何关系可得
{
x
L
˙
=
δ
˙
r
L
x
R
˙
=
δ
˙
r
R
r
L
=
r
R
+
d
(
22
)
\begin{cases} \dot{x_L}=\dot{\delta}r_L \\ \dot{x_R}=\dot{\delta}r_R \\ r_L=r_R+d \end{cases}(22)
⎩
⎨
⎧xL˙=δ˙rLxR˙=δ˙rRrL=rR+d(22)
解得
δ
˙
=
x
L
˙
−
x
R
˙
d
(
23
)
\dot{\delta}=\frac{\dot{x_L}-\dot{x_R}}{d}(23)
δ˙=dxL˙−xR˙(23)
进一步可得
δ
¨
=
x
L
¨
−
x
R
¨
d
(
23
)
\ddot{\delta}=\frac{\ddot{x_L}-\ddot{x_R}}{d}(23)
δ¨=dxL¨−xR¨(23)
联立
(
20
)
(
21
)
(
24
)
(20)(21)(24)
(20)(21)(24)可得
δ
¨
=
T
L
−
T
R
r
(
m
d
+
I
d
r
2
+
2
J
δ
d
)
(
25
)
\ddot{\delta}=\frac{T_L-T_R}{r(md+\frac{Id}{r^2}+\frac{2J_{\delta}}{d})}(25)
δ¨=r(md+r2Id+d2Jδ)TL−TR(25)
状态方程
由方程
(
19
)
(
25
)
(19)(25)
(19)(25)可得系统的状态方程为
(
x
˙
x
¨
θ
P
˙
θ
P
¨
δ
˙
δ
¨
)
=
(
0
1
0
0
0
0
0
0
A
23
0
0
0
0
0
0
1
0
0
0
0
A
43
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
)
(
x
x
˙
θ
P
θ
P
˙
δ
δ
˙
)
+
(
0
0
B
21
B
22
0
0
B
41
B
42
0
0
B
61
B
62
)
(
T
L
T
R
)
(
26
)
\begin{pmatrix} \dot{x} \\ \ddot{x} \\ \dot{\theta_P} \\ \ddot{\theta_P} \\ \dot{\delta} \\ \ddot{\delta} \\ \end{pmatrix}= \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & A_{23} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & A_{43} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \begin{pmatrix} {x} \\ \dot{x} \\ {\theta_P} \\ \dot{\theta_P} \\ {\delta} \\ \dot{\delta} \\ \end{pmatrix}+ \begin{pmatrix} 0 & 0 \\ B_{21} & B_{22} \\ 0 & 0 \\ B_{41} & B_{42} \\ 0 & 0 \\ B_{61} & B_{62} \\ \end{pmatrix} \begin{pmatrix} T_L \\ T_R \end{pmatrix}(26)
x˙x¨θP˙θP¨δ˙δ¨
=
0000001000000A230A4300001000000000000010
xx˙θPθP˙δδ˙
+
0B210B410B610B220B420B62
(TLTR)(26)
状态变量
(
x
x
˙
θ
P
θ
P
˙
δ
δ
˙
)
T
({x}\ \dot{x}\ {\theta_P}\ \dot{\theta_P}\ {\delta}\ \dot{\delta})^T
(x x˙ θP θP˙ δ δ˙)T分别表示小车的位移,前进速度,车体的倾角,车体的角速度,小车的转向角以及转向速度。由于电机输出扭矩的大小不好直接控制,通过刚体定轴转动定律将其转化为两个车轮的加速度。
{
v
L
O
˙
=
r
T
L
I
v
R
O
˙
=
r
T
R
I
(
27
)
\begin{cases} \dot{v_{LO}}=\frac{rT_L}{I} \\ \dot{v_{RO}}=\frac{rT_R}{I} \\ \end{cases}(27)
{vLO˙=IrTLvRO˙=IrTR(27)
其中
v
L
O
v_{LO}
vLO为左轮无摩擦时线速度的大小,单位为
r
a
d
/
s
rad/s
rad/s
故系统的状态空间表达式变为
{
x
˙
=
A
x
+
B
u
y
=
C
x
+
D
u
(
28
)
\begin{cases} \dot{x}=Ax+Bu \\ y=Cx+Du \end{cases}(28)
{x˙=Ax+Buy=Cx+Du(28)
式中
A
=
(
0
1
0
0
0
0
0
0
A
23
0
0
0
0
0
0
1
0
0
0
0
A
43
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
)
B
=
I
r
(
0
0
B
21
B
22
0
0
B
41
B
42
0
0
B
61
B
62
)
A=\begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & A_{23} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & A_{43} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix}\ \ \ B=\frac{I}{r} \begin{pmatrix} 0 & 0 \\ B_{21} & B_{22} \\ 0 & 0 \\ B_{41} & B_{42} \\ 0 & 0 \\ B_{61} & B_{62} \\ \end{pmatrix}
A=
0000001000000A230A4300001000000000000010
B=rI
0B210B410B610B220B420B62
C = ( 1 0 0 0 0 0 0 0 1 0 0 0 ) D = 0 C=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ \end{pmatrix}\ \ \ D=0 C=(100001000000) D=0
x = ( x x ˙ θ P θ P ˙ δ δ ˙ ) u = ( v L O ˙ v R O ˙ ) x=\begin{pmatrix} {x} \\ \dot{x} \\ {\theta_P} \\ \dot{\theta_P} \\ {\delta} \\ \dot{\delta} \\ \end{pmatrix}\ \ \ u=\begin{pmatrix} \dot{v_{LO}} \\ \dot{v_{RO}} \\ \end{pmatrix} x= xx˙θPθP˙δδ˙ u=(vLO˙vRO˙)
reference
轮趣科技——基于LQR控制的平衡小车

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)