本系列文章力求以简洁易懂的文字介绍计算几何中的基本概念，使读者快速入门，故不追求难度和深度，仅起到抛砖引玉的作用。     

       在我们的计算几何中，乃至基本的几何学中我们都需要解决一类问题，那就是几何图形的面积交并，周长交并问题，在计算几何中我们也常常遇到这样的问题，在这里我们介绍一种神奇的用来解决这类问题的算法，叫做扫描线（scan line algorithm）算法，是2018年公布的计算机科学技术名词，主要倾向于线段树+离散化这类思想，然后扫描求解过程有点像积分，那么我们开始讲解扫描线。

      我们先来看一个最基础的问题： 

      看到n的数据范围是：

      看到这个以后，我们是要去打ACM的话，肯定只考虑100%的数据，因此O(n^2)的算法直接被我们抛弃，这样子主要考虑O(n)或者O(nlogn)的算法，那么就是我们今天的算法:扫描线算法，时间复杂度是O(nlogn)的，接下来讲一下这个算法的运作过程。

扫描线：假设有一条扫描线从一个图形的下方扫向上方（或者左方扫到右方），那么通过分析扫描线被图形截得的线段就能获得所要的结果（相当于是每次算出每个单位长度上的微分，最后积起来这样的一个过程）。该过程可以用线段树进行加速。

       由于都是矩形，因此运用扫描线以后，面积的求法其实可以简化为 ∑截线段长度×扫过的高度，这也是扫描线算法最基础的应用。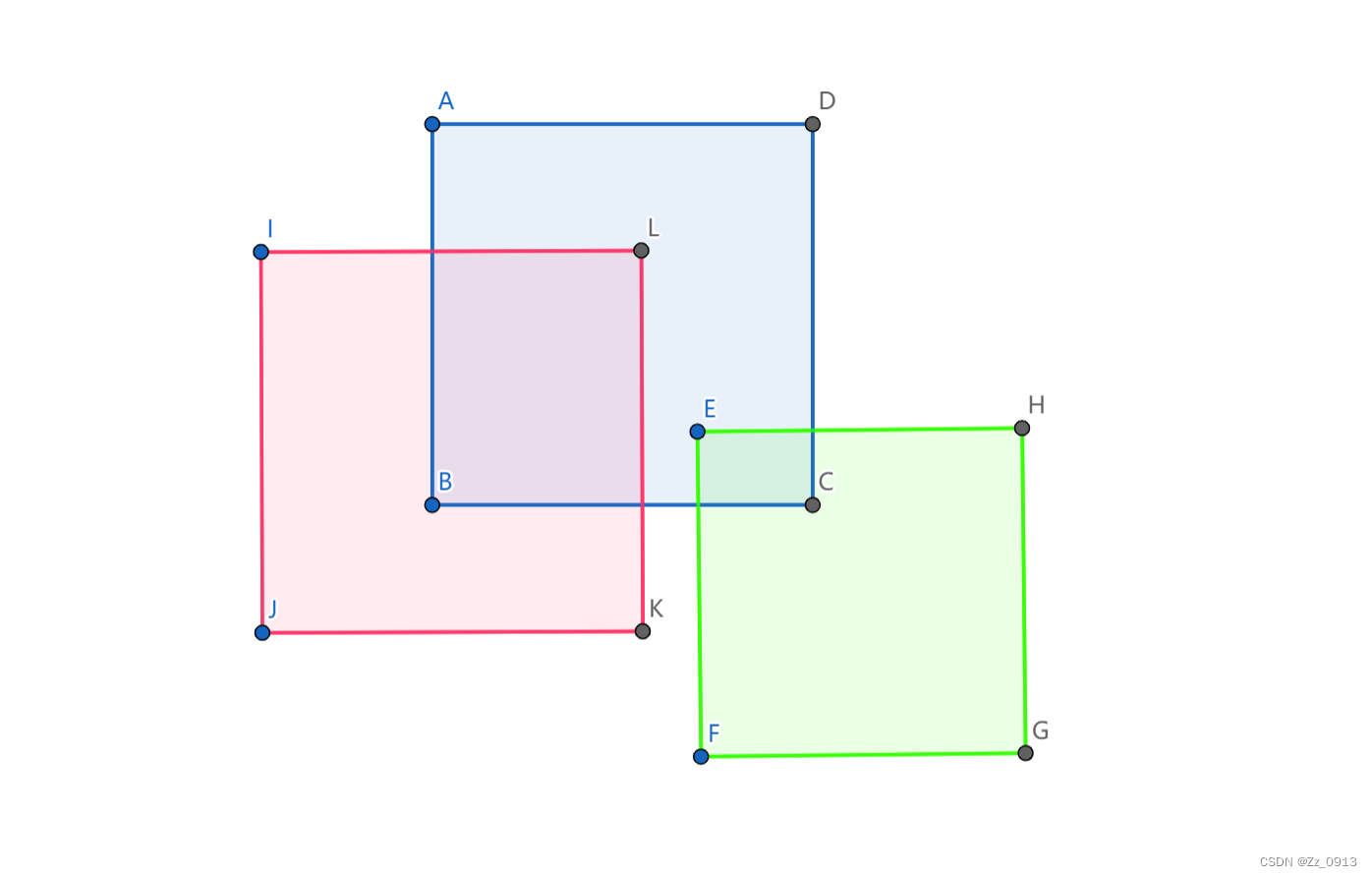

  问题在于如何才能模拟扫描线从下向上扫过图形，并且快速计算出当前扫描线被截得的长度。

  现在假设，扫描线每次会在碰到横边的时候停下来，如图👇：

      简单来说，可对图形面积产生影响的元素，也就是这些横边左右端点的坐标。那么还有一个很严重的问题就是，如何加边减边的问题，就是在某个区间怎么判断这条边还在吗？这个很简单，我们只需要在一个矩形的上下两边加上不同的权值，按照扫描方向，假如方向是从下往上，那么下方的边权就是1，上方的边权就是-1，这样子就解决了边的存在问题了：       然后把所有的横边按照矩形y坐标升序排序。这样，对于每个矩形，扫描线总是会先碰到下边，然后再碰到上边。那么就能保证扫描线所截的长度永远非负了。这样操作以后，就可以和线段树扯上关系，我们只需要在输入的时候将每个矩形的横坐标剥离出来，放在x轴上进行离散化。（其实就是把所有点的横坐标存到X[]里，然后升序排个序，最后去重。）

       👆：在这个例子中，4个端点的纵投影总共把x轴切割成了5部分。取中间的3部分线段，建立一棵线段树，其每个端点维护一条线段（也就是一个区间）的信息：

  1. 该线段被覆盖了多少次（被多少个矩形所覆盖）。
  2. 该线段内被整个图形所截的长度是多少。

      显然，只要一条线段被覆盖，那么它肯定被图形所截。所以，整个问题就转化为了一个区间查询问题，即：每次将当前扫描线扫到的边对应的信息按照之前赋上的权值更新，然后再查询线段树根节点的信息，最后得到当前扫描线扫过的面积。这就可以用线段树来实现了（线段树：顾名思义，就是树上的结点为一条条线段~），接下来我们来简单看一下模拟过程：

       1.初始化，取点存线段，建立线段树：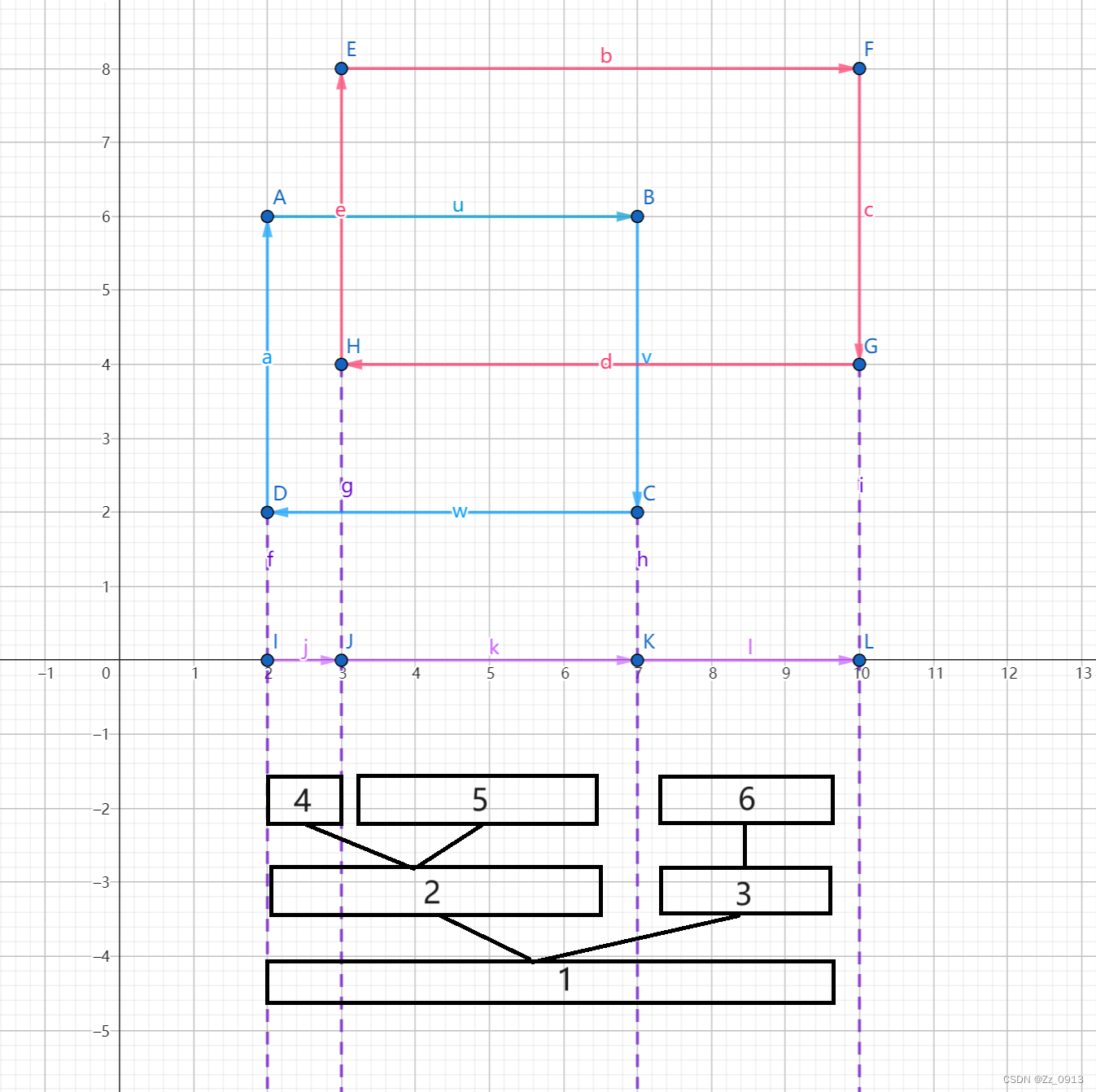

       2：扫描第一条边：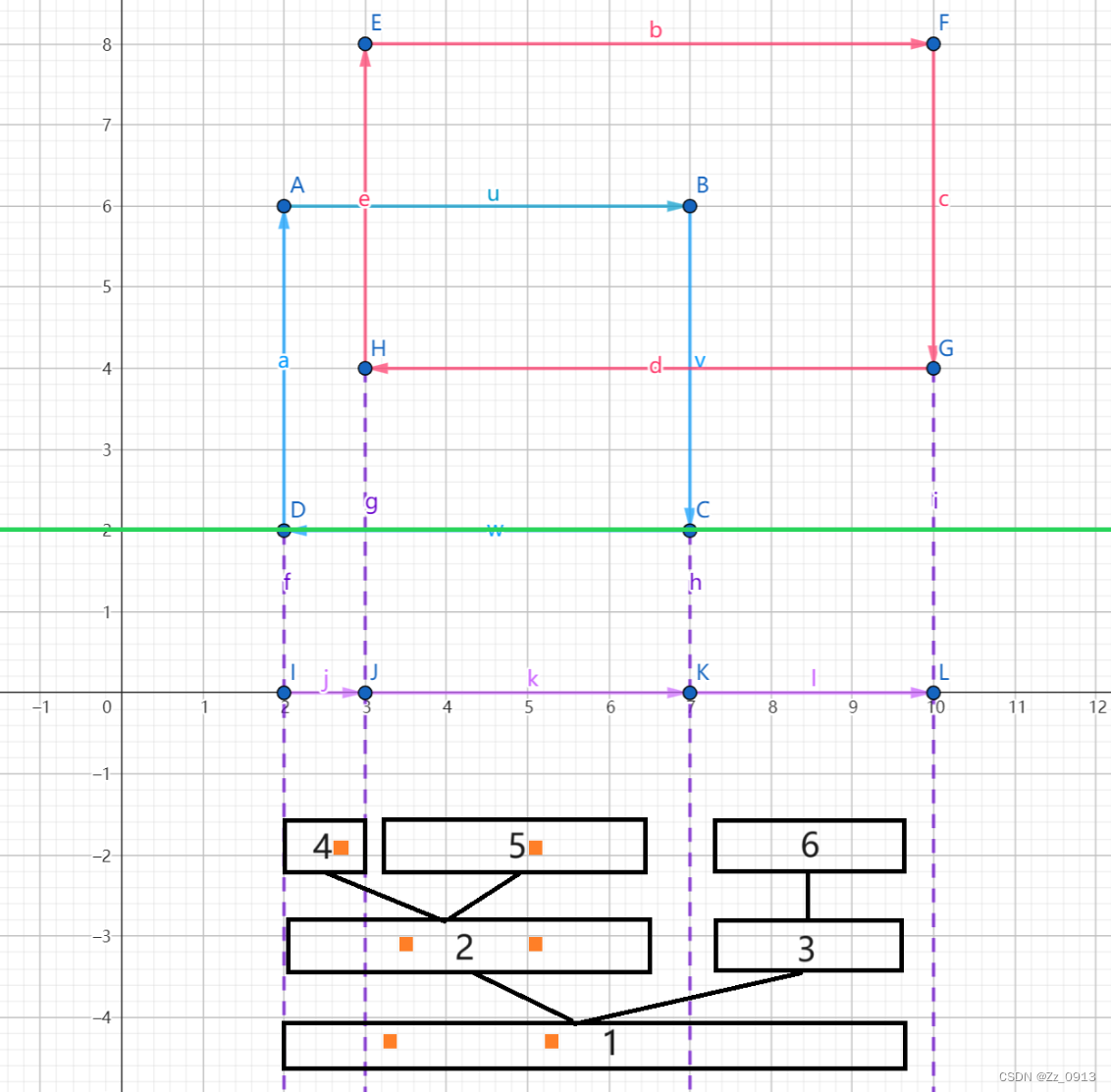

         3：扫描第二条边：

          4：扫描第三条边：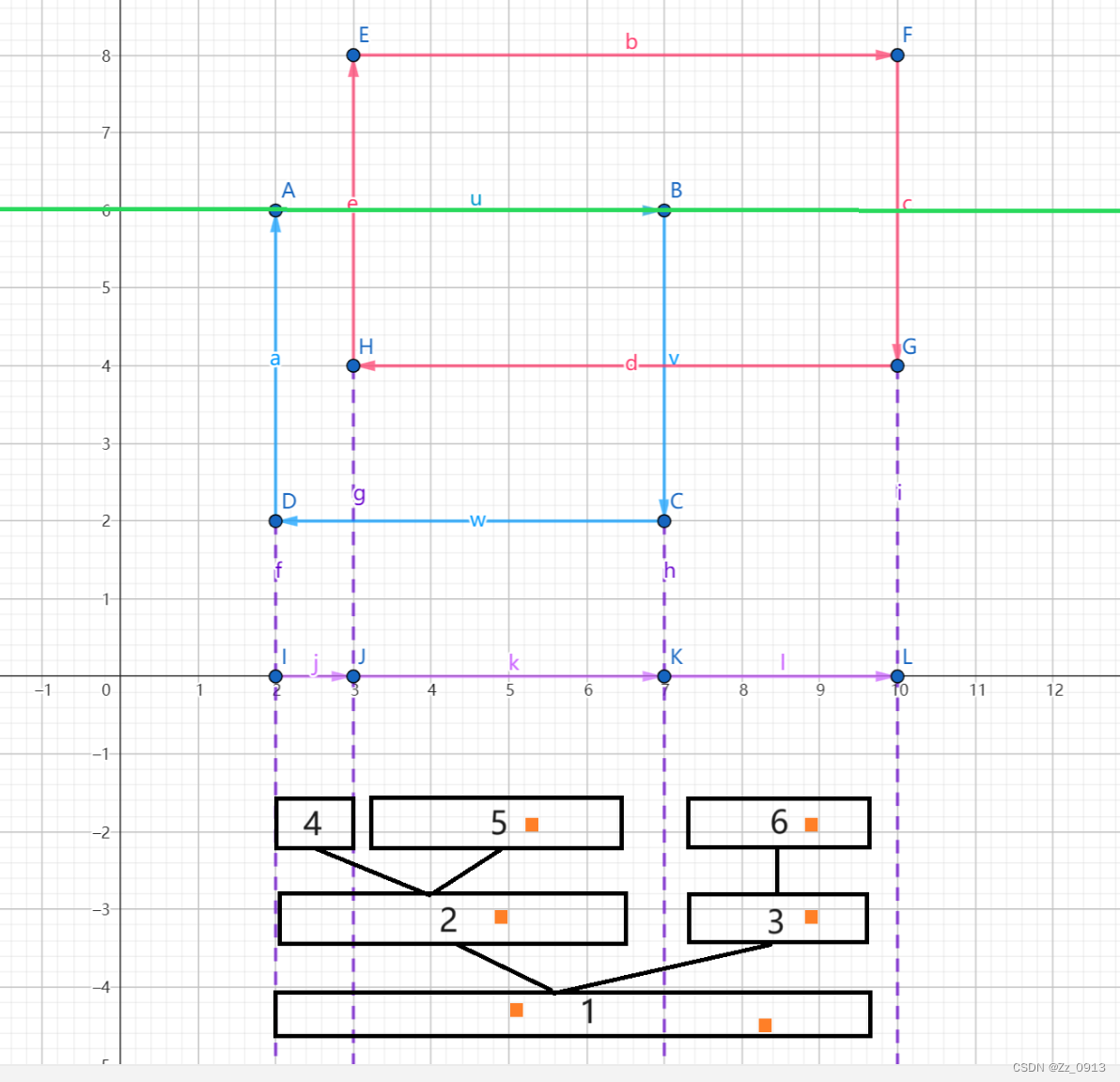

          5：扫描第四条边：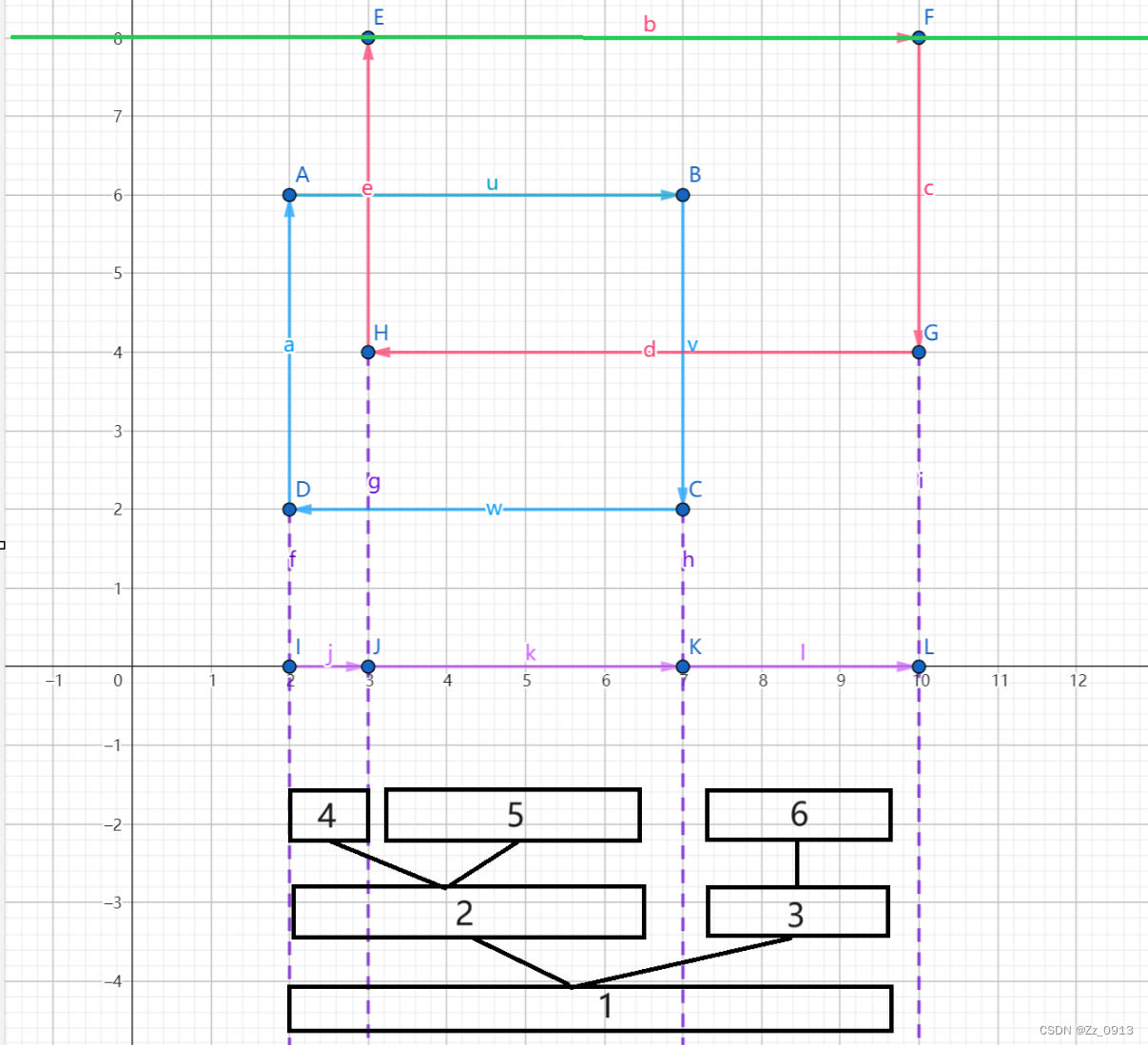

      那么对于这样的一个基本情况就是这么简单的模拟，我们只需要建立一棵线段树来存储这些线段就OK了，但是问题来了，我们应该存储线段的那些信息？这些线段应该怎么存？（开区间 or 闭区间 or 半开半闭）

      所以为了保证线段之间的兼容性，我们一般这么考虑：考虑把线段树每个节点x对应的区间（tree[x].l,tree[x].r）不变，改变区间和横边的映射关系，具体为：节点x对应[X[tree[x].l],X[tree[x].r + 1]这条横边，如果不这样想可能会出现线段之间的端点重合问题，实在是细腻啊~，所以我们建树这样子建（保存的信息还是一样，提取的时候搞一下操作）：

        然后我们只需要在更新线段树的时候做操作~：

    OK了😄，算法思路和细节方面的问题我们都解决了，接下来就看一下这个算法的板子：

#include<bits/stdc++.h>
#include<algorithm>
#define ll long long
using namespace std;
const int MAXN = 1e6 + 10;
int n,i,x1,x2,yy,y2;
int X[MAXN << 1];
inline int read1(){char ch;
	while((ch = getchar()) < '0' || ch > '9'); int res = ch - 48;
	while((ch = getchar()) >= '0' && ch <= '9') res = res * 10 + ch - 48;
	return res;}
inline long long read2(){char ch;
	while((ch = getchar()) < '0' || ch > '9'); long long res = ch - 48;
	while((ch = getchar()) >= '0' && ch <= '9') res = res * 10 + ch - 48;
	return res;}
struct ScanLine{ 
    long long l,r,h; 
	int mark; 
    bool operator<(const ScanLine &rhs) const {return h < rhs.h;}
}line[MAXN << 1];
struct SegTree{int l,r,sum; long long len; }Tree[MAXN << 2];
void Build_Tree(int k,int l,int r)
{
	Tree[k].l = l,Tree[k].r = r,Tree[k].sum = 0,Tree[k].len = 0;
	if(l == r) return;
	int mid = (l + r) >> 1;
	Build_Tree(k << 1,l,mid);
	Build_Tree(k << 1 | 1,mid + 1,r);
	return;
}
void Push_Up(int k)
{
	int l = Tree[k].l,r = Tree[k].r;
	if(Tree[k].sum) Tree[k].len = X[r + 1] - X[l];
	   else Tree[k].len = Tree[k << 1].len + Tree[k << 1 | 1].len;
}
void Update_Tree(int k,long long L,long long R,int c)
{
	int l = Tree[k].l,r = Tree[k].r;
	if(X[r + 1] <= L || X[l] >= R) return;
	if(X[l] >= L && X[r + 1] <= R)
	{
		Tree[k].sum = Tree[k].sum + c;
		Push_Up(k);
		return;
	}
	int mid = (l + r) >> 1;
	Update_Tree(k << 1,L,R,c);
	Update_Tree(k << 1 | 1,L,R,c);
	Push_Up(k);
}
int main()
{
	n = read1();
    memset(X,0,sizeof(X));
	for(int i = 1;i <= n;i++)
	{
		{x1 = read2();yy = read2();x2 = read2();y2 = read2();}
		X[2 * i - 1] = x1,X[2 * i] = x2;
		line[2 * i - 1] = (ScanLine) {x1,x2,yy,1};
		line[2 * i] = (ScanLine) {x1,x2,y2,-1};
	}
	n = n << 1;
	sort(line + 1,line + n + 1);
	sort(X + 1,X + n + 1);
	int tot = unique(X + 1,X + n + 1) - X - 1;
	Build_Tree(1,1,tot - 1);
	long long ans = 0;
	for(int i = 1;i < n;i++)
	{
		Update_Tree(1,line[i].l,line[i].r,line[i].mark);
		ans = ans + Tree[1].len * (line[i + 1].h - line[i].h);
	}
	cout<<ans<<endl;
	return 0;
}

好，我们趁热打铁（当然不是那个打铁~），再来看一道比较模板的扫描线题🤔：

     刚刚算过了矩形面积并之后，我们第一反应就可以想到截取线段，然后建立线段树维护，那么单单从下到上只能算出宽，不能算出高，所以很简单，我们再从左到右做一次同样的操作就行了~一样的道理，每次得到的贡献需要和上一次做差，表示这次新增或删除的贡献~✌

      由于每次扫描线扫描的过程和求面积并是相似的，所以这次我们不手动模拟了，那个之前忘记讲了，这个存放矩形其实也有一个结构体E（l,r,d,h):

      👆：感觉不是特别重要，但是这个计算几何的知识体系好歹完整一点😄

        OK,我们先来看看这一种做两次扫描线算法能不能再做简化，也就是只做一次扫描线，毕竟矩形的高与宽之间的联系还是非常大的，所以我们通过画图计算可以发现以下结论：

        1.纵边总长度=∑2×被截得的线段条数×扫过的高度

        2.横边总长度=∑∣上次截得的总长−现在截得的总长∣

          👆：大家可以自己模拟计算一下~

       那么事情看起来就简单很多了，我们只需要在原来线段树中存储的信息中再加上一个“线段的条数”，然后纵边和横边分开计算即可，代码如下😄：

#include<bits/stdc++.h>
#include <algorithm>
#define lson (x << 1)
#define rson (x << 1 | 1)
using namespace std;
#define Temp template<typename T>
Temp inline void read(T &x)
{
	x = 0;
	T w = 1,ch = getchar();
	while(! isdigit(ch) && ! ch == '-')
	    ch = getchar();
	if(ch == '-')
	    w = -1,ch = getchar();
	while(isdigit(ch))
	    x = (x << 3) + (x << 1) + (ch ^ '0'),ch = getchar();
	x = x * w;
}
const int MAXN = 1e5 + 10;
int n,X[MAXN << 1];
int x1,yy,x2,y2,pre = 0;
struct ScanLine{
	int l, r, h, mark;
	if(h == rhs.h) return mark > rhs.mark;
    return h < rhs.h;
}line[MAXN << 1];
struct SegTree{
	int l,r,sum,len,c;
    bool lc,rc;
}tree[MAXN << 2];
void Build_Tree(int x, int l, int r) 
{
	tree[x].l = l;
	tree[x].r = r;
	tree[x].lc = tree[x].rc = false;
	tree[x].sum = tree[x].len = 0;
	tree[x].c = 0;
	if(l == r)
		return;
	int mid = (l + r) >> 1;
	Build_Tree(lson, l, mid);
	Build_Tree(rson, mid + 1, r);
}
void Push_Up(int x) 
{
	int l = tree[x].l,r = tree[x].r;
	if(tree[x].sum) 
	{
		tree[x].len = X[r + 1] - X[l];
		tree[x].lc = tree[x].rc = true;
		tree[x].c = 1;
	}
	else 
	{
		tree[x].len = tree[lson].len + tree[rson].len;
		tree[x].lc = tree[lson].lc, tree[x].rc = tree[rson].rc;
		tree[x].c = tree[lson].c + tree[rson].c;
		if(tree[lson].rc && tree[rson].lc)
			tree[x].c -= 1;
	}
}

void Update_Tree(int x, int L, int R, int c) 
{
	int l = tree[x].l, r = tree[x].r;
	if(X[l] >= R || X[r + 1] <= L) return;
	if(L <= X[l] && X[r + 1] <= R) 
	{
		tree[x].sum += c;
		Push_Up(x);
		return;
	}
	Update_Tree(lson, L, R, c);
	Update_Tree(rson, L, R, c);
	Push_Up(x);
}

ScanLine make_line(int l, int r, int h, int mark) 
{
	ScanLine res;
	res.l = l, res.r = r,
	res.h = h, res.mark = mark;
	return res;
}
int main() 
{
	read(n);
	for(int i = 1; i <= n; i++) 
	{
		read(x1),read(yy),read(x2),read(y2);
		line[i * 2 - 1] = make_line(x1, x2, yy, 1);
		line[i * 2] = make_line(x1, x2, y2, -1);
		X[i * 2 - 1] = x1, X[i * 2] = x2;
	}
	n = n << 1;
	sort(line + 1, line + n + 1);
	sort(X + 1, X + n + 1);
	int tot = unique(X + 1, X + n + 1) - X - 1;
	Build_Tree(1, 1, tot - 1);
	int res = 0;
	for(int i = 1; i < n; i++) 
	{
		Update_Tree(1, line[i].l, line[i].r, line[i].mark);
		res = res + abs(pre - tree[1].len);
		pre = tree[1].len;
		res = res + 2 * tree[1].c * (line[i + 1].h - line[i].h);
	}
	res = res + line[n].r - line[n].l;
	cout<<res<<endl;
	return 0;
}

     👆：只能说上面求周长并的代码跟面积并的代码非常相似，可以相互比较理解一下

         那么简单的扫描线算法到这里为止，我们已经会使用扫描线算法来求得多个矩形的面积并和周长并 —— 非常基础的一些计算几何问题，当然这里还涉及到了有关线段树加速的知识，如果不了解线段树的同学通过这个算法也可以加深对线段树的理解[doge]。

         OK，上点强度~✌，接下来让我们想想除了矩形，三角形，梯形，圆这些几何图形的面积并是否也可以用扫描线求出？🤔

         👆：等腰三角形的扫描线模型

          👆：圆离散后的扫描线模型

     我们仔细看一看上面的两种模型，都是离散+扫描，经典的扫描线算法啊，可行性映入眼帘了， 所以~

         ————  答案是可以的，因为之前提过扫描线算法的思想其实接近于微积分，即求出每个单位内的微分作积，而求任何几何图形的面积，在数学里我们使用的最多的就是微积分的方法，计算几何中，我们也常常使用自适应辛普森积分公式，格林公式等微积分的方法来求相关值，所以扫描线算法这种模拟微分也是可以的，并且精度方面占点优势：

             👇：辛普森积分公式

                👇：格林公式

        这边以圆的面积并为例，我们采用三种方法，一种是采用扫描线+辛普森公式，一种是圆的离散化，还有一种是基本的几何方法~，👇选择性理解一下叭，这个还是有点难度~：

           1.圆的离散化👇：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 55;
const int MAXN = maxn * maxn + 3 * maxn;
const double Eps = 1e-10;
 
#define Temp template<typename T>
Temp inline void read(T &x)
{
    x = 0;
	T w = 1,ch = getchar();
    while(!isdigit(ch) && ch != '-')
	    ch = getchar();
    if(ch == '-')
	    w = -1,ch = getchar();
    while(isdigit(ch))
	    x = (x << 3) + (x << 1) + (ch ^ '0'),ch = getchar();
    x = x * w;
}
 
int Sign(double x) { if(fabs(x) < Eps) return 0;if(x > 0) return 1;if(x < 0) return -1;}
 
int Dcmp(double x,double y) { if(fabs(x - y) < Eps) return 0;if(x > y) return 1;if(x < y) return -1;}
 
double sqr(double x) { return x * x;}
 
struct Point{
	double x,y;
	Point(double x = 0,double y = 0) : x(x) , y(y) {};
}point[MAXN];
 
typedef Point Vector;
 
Vector operator + (Vector Alpha,Vector Beta) { return Vector(Alpha.x + Beta.x,Alpha.y + Beta.y);}
 
Vector operator - (Vector Alpha,Vector Beta) { return Vector(Alpha.x - Beta.x,Alpha.y - Beta.y);}
 
Vector operator * (Vector Alpha,double x) { return Vector(Alpha.x * x,Alpha.y * x);}
 
Vector operator / (Vector Alpha,double x) { return Vector(Alpha.x / x,Alpha.y / x);}
 
double Dis(Point Alpha,Point Beta)
{
	return sqrt(sqr(Alpha.x - Beta.x) + sqr(Alpha.y - Beta.y));
}
 
struct Tcir{
	double r;
	Point o;
};
 
struct Tinterval
{
	double x,y,Area,mid;
	int type;
	Tcir owner;
	void area(double l,double r)
	{
		double len = sqrt(sqr(l - r) + sqr(x - y));
		double d = sqrt(sqr(owner.r) - sqr(len) / 4.0);
		double angle = atan(len / 2.0 / d);
		Area = fabs(angle * sqr(owner.r) - d * len / 2.0);
	}
}inter[maxn];
double x[MAXN],l,r;
int n,N,Nn;
 
bool cmpR(Tcir Alpha,Tcir Beta)
{
	return Alpha.r > Beta.r;
}
 
void Get(Tcir owner,double x,double &l,double &r)
{
	double y = fabs(owner.o.x - x);
	double d = sqrt(fabs(sqr(owner.r) - sqr(y)));
	l = owner.o.y + d;
	r = owner.o.y - d;
}
 
void Get_Interval(Tcir owner,double l,double r)
{
	Get(owner,l,inter[Nn].x,inter[Nn + 1].x);
	Get(owner,r,inter[Nn].y,inter[Nn + 1].y);
	Get(owner,(l + r) / 2.0,inter[Nn].mid,inter[Nn + 1].mid);
	inter[Nn].owner = inter[Nn + 1].owner = owner;
	inter[Nn].area(l,r),inter[Nn + 1].area(l,r);
	inter[Nn].type = 1,inter[Nn + 1].type = -1;
	Nn = Nn + 2;
}
bool cmp(Tinterval Alpha,Tinterval Beta)
{
	return Alpha.mid > Beta.mid + Eps;
}
void Add(double xx)
{
	x[N] = xx;
	N = N + 1;
}
double dist2(Point Alpha,Point Beta)
{
	return sqr(Dis(Alpha,Beta));
}
Point Rotate(Point p,double cost,double sint)
{
	double x = p.x,y = p.y;
	return Point(x * cost - y * sint,x * sint + y * cost);
}
pair<Point,Point>crosspoint(Point ap,double ar,Point bp,double br)
{
	double d = (ap - bp).norm();
	double cost = (ar * ar + d * d - br * br) / (2 * ar * d);
	double sint = sqrt(1. - cost * cost);
	Point v = (bp - ap) / (bp - ap).norm() * ar;
	return make_pair(ap + Rotate(v,cost,-sint),ap + Rotate(v,cost,sint));
}
double getUnion(int n,Tcir a[])
{
	int p = 0;
	sort(a,a + n,cmpR);
	for(int i = 0;i < n;i++)
	{
		bool f = true;
		for(int j = 0;j < i;j++)
		if(dist2(a[i].o,a[j].o) <= sqr(a[i].r - a[j].r) + Eps)
		{
			f = false;
			break;
		}
		if(f == true)
		{
			a[p] = a[i];
			p = p + 1;
		}
	}
	n = p;
    N = 0;
    for(int i = 0;i < n;i++)
    {
    	Add(a[i].o.x - a[i].r);
        Add(a[i].o.x + a[i].r);
        Add(a[i].o.x);
        for(int j = i + 1;j < n;j++)
        if(dist2(a[i].o,a[j].o) <= sqr(a[i].r + a[j].r) + Eps)
		{
			pair<Point,Point> cross=crosspoint(a[i].o,a[i].r,a[j].o,a[j].r);
			Add(cross.first.x);
			Add(cross.second.x);
		} 
	}
	sort(x,x + N);
	p = 0;
	for(int i = 0;i < N;i++)
	if(! i || fabs(x[i] - x[i - 1]) > Eps) 
	{
		x[p] = x[i];
		p = p + 1;
	}
	N = p;
	
	double ans = 0;
	for(int i = 0;i + 1 < N;i++)
	{
		l = x[i],r = x[i + 1];
		Nn = 0;
		for(int j = 0;j < n;j++)
		if(fabs(a[j].o.x - l) < a[j].r + Eps && fabs(a[j].o.x - r) < a[j].r + Eps)
		    Get_Interval(a[j],l,r);
		if(Nn)
		{
			sort(inter,inter + Nn,cmp);
			int cnt = 0;
			for(int i = 0;i < Nn;i++)
			{
				if(cnt > 0)
				{
					ans = ans + (fabs(inter[i - 1].x - inter[i].x)
					          + fabs(inter[i - 1].y - inter[i].y)) * (r - l) / 2.0;
					ans = ans + inter[i - 1].type * inter[i - 1].Area;
					ans = ans - inter[i].type * inter[i].Area;
				}
				cnt = cnt + inter[i].type;
			}
		}
	}
	return ans;
}
 
int main()
{
	read(n);
	Tcir Circle[MAXN];
	for(int i = 0;i < n;i++)
	{
		double xxx,yyy,rrr;
		scanf("%lf%lf%lf",&xxx,&yyy,&rrr);
		Circle[i].o.x = xxx,Circle[i].o.y = yyy;
		Circle[i].r = rrr;
	}
	printf("%.10f\n",getUnion(n,Circle));
	return 0;
}

         2：👇基本的几何方法：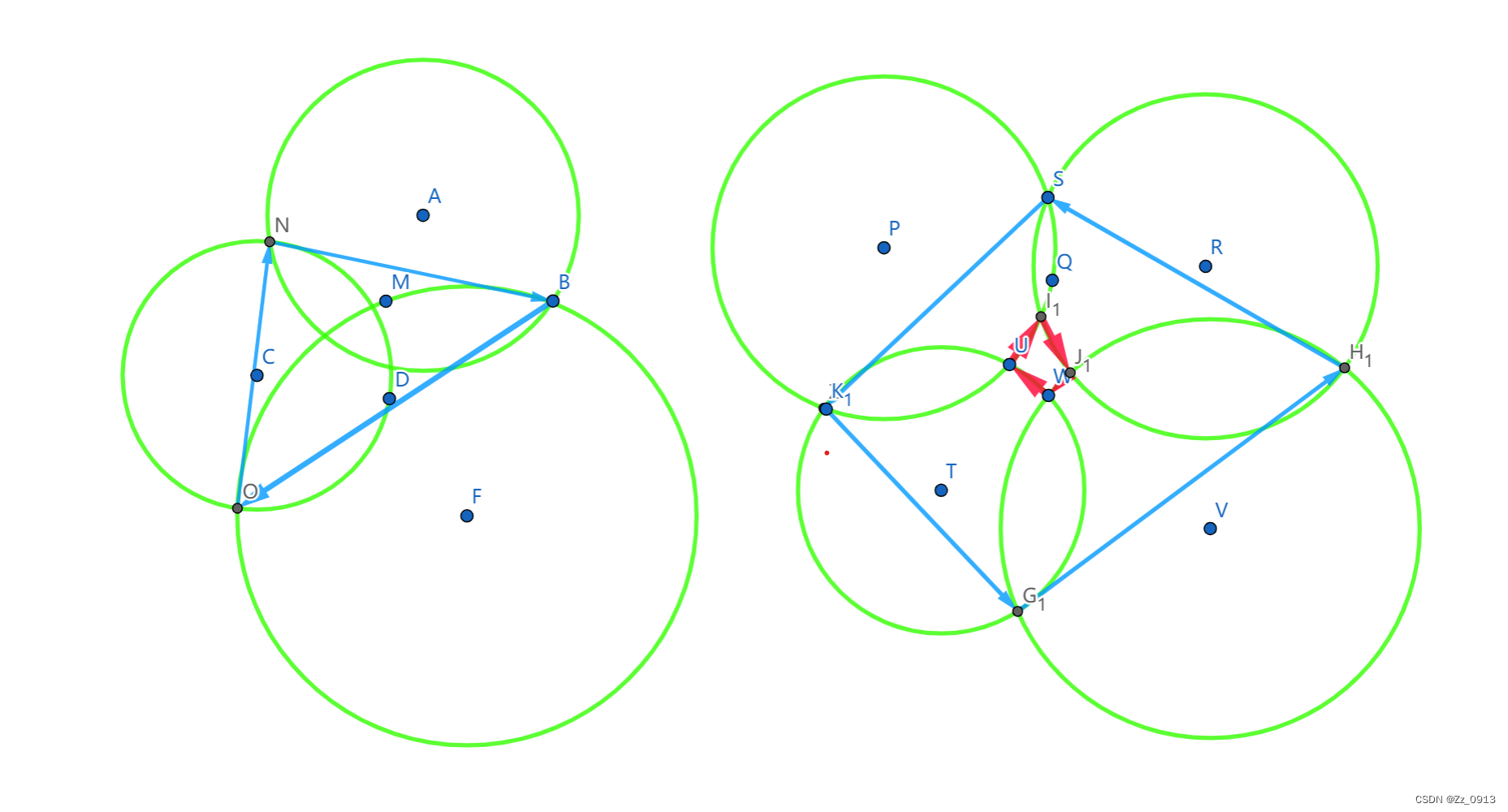

    1.如图所示，将圆的面积剖分成若干个多边形的面积与若干个弓形的面积。多边形的边就是圆的交点构成的不被其他圆覆盖的弦。计算有向面积的话，可以看到中间“洞”的面积恰好被顺时针的多边形包围，因此会被减去。请注意，必须去重复的圆，否则答案会有重复计算的面积。

        代码：

double Cross(Point Alpha,Point Beta)
{
	return Alpha.x * Beta.y - Alpha.y * Beta.x;
}
struct Circle{
	Point p;
	double r;
	bool operator < (Circle o)
	{
		if(Sign(r - o.r) != 0) return Sign(r - o.r) == -1;
		if(Sign(p.x - o.p.x) != 0)
		{
			return Sign(p.x - o.p.x) == -1;
 		}
		return Sign(p.y - o.p.y) == -1;
	}
	bool operator == (Circle o)
	{
		return Sign(r - o.r) == 0 && Sign(p.x - o.p.x) == 0 && Sign(p.y - o.p.y) == 0;
	}
}; 
inline pair<Point,Point>crosspoint(Circle Alpha,Circle Beta)
{
	return crosspoint(Alpha.p,Alpha.r,Beta.p,Beta.r);
}
Circle c[1000],tc[1000];
int n,m;
struct Node{
	Point p;
	double a;
	int d;
	Node(Point p,double a,int d) : p(p) , a(a) , d(d) {}
	bool operator < (Node o) 
	{
		return a < o.a;
	}
};
double arg(Point p)
{
	return arg(complex<double>(p.x,p.y));
}
double solve()
{
	sort(tc,tc + m);
	m = unique(tc,tc + m) - tc;
	for(int i = m - 1;i >= 0;i--)
	{
		bool ok = true;
		for(int j = i + 1;j < m;j++)
		{
			double d = (tc[i].p - tc[j].p).norm();
			if(Sign(d - abs(tc[i].r - tc[j].r)) <= 0)
			{
				ok = false;
				break;
			}
		}
		if(ok == true) 
		{
			c[n] = tc[i];
			n = n + 1;
		}
	}
	double ans = 0;
	for(int i = 0;i < n;i++)
	{
		vector<Node> event;
		Point boundary = c[i].p + Point(-c[i].r,0);
		event.push_back(Node(boundary,-pi,0));
		event.push_back(Node(boundary,pi,0));
		for(int j = 0;j < n;j++)
		{
			if(i == j) continue;
			double d = (c[i].p - c[j].p).norm();
			if(Sign(d - (c[i].r + c[j].r)) < 0)
			{
				pair<Point,Point> ret = crosspoint(c[i],c[j]);
				double x = arg(ret.first - c[i].p);
				double y = arg(ret.second - c[i].p);
				if(Sign(x - y) > 0)
				{
					event.push_back(Node(ret.first,x,1));
					event.push_back(Node(boundary,pi,-1));
					event.push_back(Node(boundary,-pi,1));
					event.push_back(Node(ret.second,y,-1));
				}else
				{
					event.push_back(Node(ret.first,x,1));
					event.push_back(Node(ret.second,y,-1));
				}
			}
		}
		sort(event.begin(),event.end());
		int sum = event[0].d;
		for(int j = 1;j <(int)event.size();j++)
		{
			if(sum == 0)
			{
				ans = ans + cross(event[j - 1].p,event[j].p) / 2;
				double x = event[j - 1].a;
				double y = event[j].a;
				double area = c[i].r * c[i].r * (y - x) / 2;
				Point v1 = event[j - 1].p - c[i].p;
				Point v2 = event[j].p - c[i].p;
				area = area - Cross(v1,v2) / 2;
				ans = ans + area;
			}
		}
	}
	return ans;
}

          3：辛普森积分👇：

 

      那么小有难度的圆的面积并也被我们轻松解决了，ok，这篇博文实在是有点长了，再讲三角形和梯形就没必要了毕竟大家思路都懂了对叭~[doge] ，所以给几道可以去试试的例题：

           三角形 - 洛谷

           [HNOI2012] 三角形覆盖问题 - 洛谷 

           POJ 1177

           POJ 1151 

    这个扫描线算法小有难度但是真的很有趣啊，跟旋转卡壳一样有趣不是吗[doge]，我要好好学旋转卡壳辣，今天就先到这里~

# 算法 # 几何学 # c++ # c语言 # 青少年编程 # 推荐算法 # 数据结构
Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

cover

赛项征集 | 第二届开放原子开源大赛——汽车软件开源赛火热进行中

avatar 开放原子开发者工作坊

开放原子校源行启动优质开源课程征集，助力高校开源人才培养

校源行启动优质开源课程征集，助力高校开源人才培养

avatar 开放原子开发者工作坊
cover

第二届Open Source Congress在北京成功举办

avatar 开放原子开发者工作坊