网络放大器
网络放大器问题描述对于一个石油传送网络可由一个加权有向无环图G表示。该图中有一个称为源点的顶点S ( 保证S的入度为0 ) , 从S出发 , 石油流向图中的其他顶点 . G中每条边上的权重为它所连接的两点间的距离。在输送石油的过程中 , 需要有一定的压力才能使石油从一个点到达另一个点,但压力会随着路程的增加而降低 ( 即压力的损失量是路程的函数 ) .因此为了保证石油在网络的正常运输,在网络传输中
网络放大器
问题描述
对于一个石油传送网络可由一个加权有向无环图G表示。该图中有一个称为源点的顶点S ( 保证S的入度为0 ) , 从S出发 , 石油流向图中的其他顶点 . G中每条边上的权重为它所连接的两点间的距离。
在输送石油的过程中 , 需要有一定的压力才能使石油从一个点到达另一个点,但压力会随着路程的增加而降低 ( 即压力的损失量是路程的函数 ) .
因此为了保证石油在网络的正常运输,在网络传输中必须保证在任何位置的压力都要不小于最小压力Pmin。为了维持这个最小压力,可在G中的一些或全部顶点放置压力放大器 , 压力放大器可以将压力恢复至该网络允许的最大压力Pmax。
可以设d为石油从压力Pmax降为压力Pmin所走的距离 , 在无压力放大器的情况下石油可运输的距离不超过d .
在该问题中 , 需要在G中放置最少的压力放大器 , 使得该传输网络从S出发,能够将汽油输送到图中的所有位置。
基本要求
1.针对该问题做出一定的合理分析和假设
2.确定输入的数据格式并给出数据生成器.
3.给出两种方法以解决上述问题,思考如何验证两种方法的正确性.
4.比较两种方法的时间和空间性能,用图表显示比较结果。
已经实现
- 使用分支定界和回溯解决了问题。
- 对程序的正确性有推导或对比: 将对拍程序封装成函数,并且验证了两个方法的正确性.
- 合理且完善的性能分析与图表展示: 使用python的matplotlib 实现了时间和空间性能用图表显示比较结果,进行了分析。
- 用库cyaron的数据生成器make.py 生成了部分数据进行了测试
- 使用dot作图的方法,实现了图的可视化方便验证正确性,可以直观的展示程序的结果 , 包括放大器的位置 , 每个位置的压力 , 边权等.
- 程序设计规范,封装良好,拥有详细的注释。
- 压缩包包括solution1.h solution2.h graph.h main.cpp 以及生成图表的testRoom.py testtime.py make.py
- GitHub实验代码
部分展示
一次跑完100个样例并且输出到文件,包括性能分析图表、每个样例的图片!


性能分析图表,时间和空间


结构
- graph.h 定义图结构DAG以及用于分支定界的子集树
- solution1.h 回溯算法实现
- sooluton2.h 分支定界算法实现
- main.cpp Drive Program
可视化
void visualize(int i)
使用dot作图 的方式进行画图验证正确性,只需要输入描述性语言,例如图的节点以及信息,边的信息,执行dot命令 就可以画出每个样例的图的信息的图片。
最后进行系统调用,把dot 作图成为jpg
void DAG::visualize(int i)
{//可视化
recountpre();
//system("cd C:\\Users\\12042\\Desktop\\dagData\\outputimage");
string name = to_string(i) + ".dot";
std::ofstream out(name);
out << "digraph g {\n";
for (int i = 1; i < nodes.size(); i++) {
out << i;
if (place_bst[i])
out << "[label=\"node" << i << ";pre = " << nodes[i].press << "\",style=filled, fillcolor=red];\n";
else
out << "[label=\"node" << i << ";pre = " << nodes[i].press << "\",style=filled, fillcolor=white];\n";
}
for (auto i = 1; i <= n; ++i) {
for (auto& edge : nodes[i].edges) {
out << i << "->" << edge.to << "[label=\"cost=" << edge.cost << "\"];\n";
}
}
out << "}\n";
out.close();
string order = "dot -Tjpg " + to_string(i) + ".dot -o solve" + to_string(i) + ".jpg";
system(order.c_str());
}
对拍
void check()
对拍程序即对自己程序的输出文件与标准(正确)答案的输出文件进行答案比对,如果完全相同,则证明正确性上没有问题,如果有不同,则证明正确性无法保证。 通常是单独写一个cpp文件,然后执行exe,鉴于本实验输出结果每个样例有且只有一个数字,所以把他封装成函数,每次输入STDOUTPUT的结果和自己的结果进行挨个比对,进行对拍即可!
void check() {
int flag = 0;
stringstream ss;
for (int i = 1; i <= 100; i++) {
cout << "正在测试数据集: " << i << "\n";
string opstd = "C:\\Users\\12042\\Desktop\\dagData\\outputSTD\\";
string myin = "C:\\Users\\12042\\Desktop\\dagData\\output\\";
opstd += to_string(i) + ".out";
myin += to_string(i) + ".out";
ifstream finstd(opstd);
if (!finstd.is_open()) {
cout << "文件打开失败\n";
}
int ans; finstd >> ans;
finstd.close();
ifstream finmy(myin);
if (!finmy.is_open()) {
cout << "文件打开失败\n";
}
int me; finmy >> me;
finmy.close();
if (me != ans) {
cout << "Wrong Answer\n";
ss << i << "WA!\n";
flag = 1;
}
else {
cout << "Accept\n";
}
}
if (!flag) {
cout << "All Accept!\n";
}
else cout << "Wrong Answer\n";
cout << ss.str();
}
基本算法
void topsort() 拓扑排序
因为各个顶点之间存在着前后关系,并且有源点,所以为了布置好放大器,必须要建立一个拓扑序列,根据拓扑序列进行油压的检测以及放大器的放置的判断。
具体思路:
①每次找出入度为0的点
②将这些顶点以及他们的出边删除
③记录删除的顺序作为拓扑序列。
④更新受影响的点的入度。
⑤重复1-4直到每个点都确定了一个拓扑次序。
void DAG::topsort()
{//确定一个拓扑序列 以便后续
int cnt = 1;
queue<int> q;
for (int i = 1; i <= n; i++) {
if (in_deg[i] == 0) q.push(i);
}
while (!q.empty()) {
int u = q.front(); q.pop();
nodes[u].toponum = cnt;
dig[cnt++] = u;//排序
for (auto e : nodes[u].edges) {
if (--in_deg[e.to] == 0)
q.push(e.to);
}
}
if (cnt < n) {
cout << "图中有环路!不符合要求!\n";
return;
}
//for (int i = 1; i <= n; i++)
//cout << "top " << i << " " << dig[i] << "\n";
}
回溯算法
第一种解决算法是使用回溯+剪枝的方式解决放大器放置的问题
回溯是按照DFS的策略从根节点开始出发,搜索解空间树(决策树),每个点都有可能放置或者不放置放大器,而这样的复杂度是 O ( 2 n ) O(2^n) O(2n) 为了降低复杂度,就必须使用剪枝函数,在搜索最优解的过程中对解空间进行剪枝,例如确定某点必须放置,或者确定某解空间必定不为最优解等等,来减少解空间的搜索次数。
具体思路
void DAG::backtracking(int level, int cnt)
level 是 搜索层数,n是节点个数,cnt是放置的放大器个数,best是指迄今为止记录的最优解
①level >= n时便求得了一个解,如果此时的cnt 更小,则是一个更优解,进行更新最优解的操作。
②如果level < n-1, 当前扩展的节点有两种可能,放置或者不放置,如果该点向其他点输送时,有的点油压<PMIN,则该点必须放置,剪掉不放置的情况,进行递归和回溯。其次,如果该点的油压<Pmin 则该点必须放置,剪掉不放置的情况,进行递归和回溯。否则,需要进行放置和不放置的两个决策的递归。
剪枝:
①如果在某层决策的时候,cnt以及大于best了,则不需要进行决策了,因为必然不是最优解。
②如果某点PRESS < PMIN 则必须放。 但是,事实上,从前向后按拓扑序决策,前面的决策已经保证了该点的油压>Pmin了,所以此种情况不会遇到!
③如果送去相邻节点PRESS < PMIN,必须放增压器,不需要考虑不放!
注意 :如果某点油压>=PMAX 或者说到其他节点都符合要求,也要考虑放置放大器,因为求最优解,此处不放置可能导致后面多个子节点放置,导致求出不为最优解的情况,所以两个决策都要考虑!
数据结构
回溯方法,需要考虑解空间树(决策树) 但是不需要实际建立,需要在每次决策中体现出来即可。之后维护level cnt分别作为决策的深度,以及放置的个数,用来剪枝和确定最优解。邻接表的表头node 存储每个点的信息,例如press 以及 booster,最后需要把信息输入到place_booster 数组,确定哪些点放了放大器。
// 回溯需要按照拓扑序跑! dfs
void DAG::backtracking(int level, int cnt)
{//进行回溯决策树里面 左是该节点不放 右子树是放
//搜索第level层
int u = dig[level];//当前点 level也代表了拓扑序
if (level >= n) {//最底层了
best_ans = min(cnt, best_ans);
//记录下最好的情况 不然会被冲了
//更新放置情况
for (int i = 1; i <= n; i++) {
place_bst[i] = false;
place_bst[i] = nodes[i].booster;
}
return;
}
if (level == 1) {//第一层 源点肯定放了(不算)只需要判断其他边 如果低了 就在v放
backtracking(2, 0);
}
else {//其他层 如果到v 不行 则在 u放
int j;
int flag = 0;
int temp_pre = -1;//临时变量pre 用来回溯!
//求press[u] 优化 用入边
//for (auto& c : nodes[u].inedges) {
// int f = c.from;
// if (nodes[f].toponum < nodes[u].toponum)
// {//必须是拓扑序前面的
// temp_pre = max(temp_pre, nodes[u].press - c.cost);
// }
//}
for (int k = 1; k < level; k++) {//求 前面到
for (auto& x : nodes[dig[k]].edges) {
if (x.to == u)
//nodes[u].press = max(nodes[u].press, nodes[dig[k]].press - x.cost);
temp_pre = max(temp_pre, nodes[dig[k]].press - x.cost);
}
}
for (j = 0; j < 2; j++)
{//进行两种决策
//剪枝1
if (temp_pre >= Pmax) {
backtracking(level + 1, cnt);
break;
}
//剪枝2
if (temp_pre < Pmin)
{
cnt++;
nodes[u].booster = true;
//剪枝3
if (cnt >= best_ans) {
return;
}
backtracking(level + 1, cnt);
}
if (j == 0) {//不放 但是需要
for (auto& v : nodes[u].edges) {//对于所有出边进行判断
int next_pr = temp_pre - v.cost;
if (next_pr < Pmin) {
flag = 1;
break;
}
}
}
//决策 put
if (j == 1 || flag == 1) {//放
cnt++;
nodes[u].press = Pmax;
nodes[u].booster = true;
//剪枝
if (cnt >= best_ans)
return;
else {
backtracking(level + 1, cnt);
}
}
//not put
else if (j == 0) {//对应的 j==0 && flag!=1
nodes[u].press = temp_pre;
nodes[u].booster = false;
backtracking(level + 1, cnt);
}
}
}
}
分支定界
最小耗费的优先队列 分支定界求解
分支定界采用子集树来表示解空间,但是每个活结点只有一次机会成为扩展结点,活结点一旦成为扩展节点,就会产生所有的儿子节点,不可能行的都丢弃。使用最小耗费分支定界的限界函数来进行生成和展开活结点数量。每次确定最小耗费的下限,即最少的cnt数。
具体思路
①最开始的活结点是根节点,之后求活结点的子节点进行判断其能否作为扩展结点。
②求出子节点压力,如果子节点有不符合要求的,则必须把该节点作为扩展结点,如果他符合不油压要求,则cnt++,作为活结点,否则两种情况作为活结点,直到level == n-1结束(最后一个一定不put)
数据结构
使用一个子集树节点 subsetnode (btnode) 里面存储每个扩展结点的父节点,即从哪来的,press,level,是否放放大器,以及bstnum,该路上已经放了多少个booster,以此max_to_cost,用来减少复杂度限界使用!之后进行求解,使用优先队列存储子集树节点,按照bstnum排序,最后求出的第一个level = n-1的解,即最优解!
//最小耗费 分支定界
void DAG::branch_bound()
{//分支定界 活结点--扩展结点-- 子集空间树
btnode* enode = new btnode(Pmax, 2);//活结点
int level = 2;
while (level <= n - 1)
{//进行活结点的拓展
int vert = dig[level];//该层扩展的节点
int temp_press = -1;
int flag = 0;
//求扩展结点的压力
for (int k = 1; k <= level - 1; k++) {
for (auto& e : nodes[dig[k]].edges) {
if (e.to == vert) {
btnode* p = enode;
//????
for (int j = level - 1; j > k; j--)
p = p->parent;
temp_press = max(temp_press, p->press - e.cost);
}
}
}
//限界函数 -最大花费 小必须放
if (temp_press - nodes[vert].max_to_cost < Pmin) {
flag = 1;
}
//check 到 邻接点是否符合要求
/*for (auto& e : nodes[vert].edges) {
if (temp_press < Pmin + e.cost) {
flag = 1; break;
}
}*/
if (flag == 0) {//两种 放或者放
btnode* t = new btnode(temp_press, level + 1, enode, enode->bstnum);
pq.push(t);
btnode* tt = new btnode(Pmax, level + 1, enode, enode->bstnum + 1);
tt->bst_here = true;
pq.push(tt);
}
else {//必须放
btnode* tt = new btnode(Pmax, level + 1, enode, enode->bstnum + 1);
tt->bst_here = true;
pq.push(tt);
}
enode = pq.top(); pq.pop();
level = enode->level;
}
best_ans = enode->bstnum;
btnode* p = enode;
while (p) {
place_bst[dig[p->level - 1]] = p->bst_here;
p = p->parent;
}
}
性能分析
进行性能对比,在跑每个样例的过程中记录一下时间,输出到文件中,并且计算每个样例所用的空间大小,输出到文件。
使用Python matplotlib作图,做出折线图对比性能。 使用LARGE_INTEGER + QueryPerformanceCounter() 统计时间
统计时间
LARGE_INTEGER start_time; //开始时间
LARGE_INTEGER end_time; //结束时间
double dqFreq; //计时器频率
LARGE_INTEGER freq; //计时器频率
QueryPerformanceFrequency(&freq);
dqFreq = (double)freq.QuadPart;
QueryPerformanceCounter(&start_time); //计时开始
DAG g;
g.topsort();
g.backtracking(1, 0);
fout << g.best_ans << "\n";
QueryPerformanceCounter(&end_time); //计时end
// write out!
ofstream fo("cost1.txt", ios::app);
double run_time = (end_time.QuadPart - start_time.QuadPart) / dqFreq * 1000;
fo << i << " " << run_time << "\n";
fo.close();
//空间 第一种 回溯
ofstream foo("room1.txt", ios::app);
//int 4 bool 1
ll romcost = 5 * g.n + 4 * g.m + 4 * g.n;
foo << i << " " << romcost << "\n";
foo.close();
测试time并画图的Python代码
import matplotlib.pyplot as plt
input_txt = 'cost1.txt'
x = []
y = []
z = []
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
x.append(int(line[0]))
y.append(float(line[1]))
f.close
input_txt = 'cost2.txt'
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
z.append(float(line[1]))
f.close
plt.plot(x, y, marker='o', label='backtrack')
plt.plot(x, z, marker='*', label='branch_bound',linestyle="--")
plt.xticks(x[0:len(x):2], x[0:len(x):2], rotation=45)
plt.margins(0)
plt.xlabel("data")
plt.ylabel("cost(ms)")
plt.title("compare time")
plt.tick_params(axis="both")
plt.legend()
plt.show()
测试空间性能并画图的Python代码,空间性能是我大致根据字节数计算的,没找到如何测量
import matplotlib.pyplot as plt
input_txt = 'room1.txt'
x = []
y = []
z = []
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
x.append(int(line[0]))
y.append(int(line[1]))
f.close
input_txt = 'room2.txt'
f = open(input_txt)
for line in f:
line = line.strip('\n')
line = line.split(' ')
z.append(int(line[1]))
f.close
plt.plot(x, y, marker='o', label='backtrack')
plt.plot(x, z, marker='*', label='branch_bound',linestyle="--")
plt.xticks(x[0:len(x):2], x[0:len(x):2], rotation=45)
plt.margins(0)
plt.xlabel("data")
plt.ylabel("cost(Byte)")
plt.title("compare roomspace")
plt.tick_params(axis="both")
plt.legend()
plt.show()
结果展示
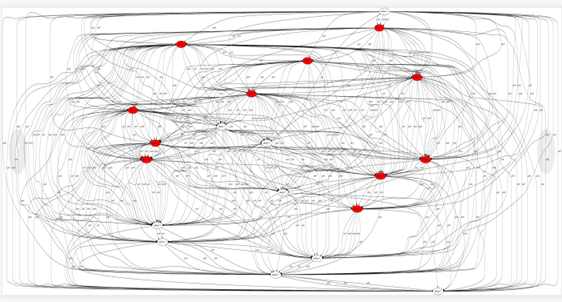
生成DAG的图片

具体DAG图片,红色mark 放大器的位置


结果分析
复杂度
回溯和分支定界:时间复杂度都为O(2^n),但是经过剪枝和限界之后会远小于这个复杂度。
性能表现
回溯法和分支定界法,这两个算法都需要有一个限界函数,并且设计思想类似。对于这两个算法,时间复杂度都是O(2^n),虽然复杂度一样,但是在具体问题特别是数据较多的时候,由于回溯法即使找到了最优解也不能马上就肯定他是最优的,必须把所有可行解都求出来才能确定。而分支定界,只需要找到一个解,这个解必为最优的。分支定界比回溯法检查更少的情况和节点,时间性能更好。
但是在空间性能上:回溯法如果建立解空间的话,使用的内存是O(n)即最长路径的空间大小,而分支定界占用的内存为O(2^n)加之回溯法不需要真的建立节点,而分支定界需要建立节点,又多了一层空间代价。

在回溯时,如果一个节点>Pmax并且临界点都>Pmin 不能直接剪去放置的情况,经过实验发现,Vi没放置,但是他的下一个临界点Vi+1 Vi+2… 可能会因为他们的下一个节点而放置,也就是放置了>1个。此时如果Vi 放置了,会提升他们的Press,可能他不需要额外放置,所以总共放置了1个,所以需要对两种决策都进行递归回溯。为此,我也删除了我的一个剪枝函数,才得到了最优解。
改进
- 可以尝试暴力算法求解
- 剪枝算法可以进一步优化剪枝,提高效率
- 在数据结构方面,或许可以考虑图结构的反转 ,根据使用频率来优化数据结构
- 计算所需空间性能,可以思考如何度量
- 优化整体项目结构,(现在回看写的太chou了~)
定他是最优的,必须把所有可行解都求出来才能确定。而分支定界,只需要找到一个解,这个解必为最优的。分支定界比回溯法检查更少的情况和节点,时间性能更好。
但是在空间性能上:回溯法如果建立解空间的话,使用的内存是O(n)即最长路径的空间大小,而分支定界占用的内存为O(2^n)加之回溯法不需要真的建立节点,而分支定界需要建立节点,又多了一层空间代价。
[外链图片转存中…(img-Zi8B3xRG-1651889072411)]
在回溯时,如果一个节点>Pmax并且临界点都>Pmin 不能直接剪去放置的情况,经过实验发现,Vi没放置,但是他的下一个临界点Vi+1 Vi+2… 可能会因为他们的下一个节点而放置,也就是放置了>1个。此时如果Vi 放置了,会提升他们的Press,可能他不需要额外放置,所以总共放置了1个,所以需要对两种决策都进行递归回溯。为此,我也删除了我的一个剪枝函数,才得到了最优解。
改进
- 可以尝试暴力算法求解
- 剪枝算法可以进一步优化剪枝,提高效率
- 在数据结构方面,或许可以考虑图结构的反转 ,根据使用频率来优化数据结构
- 计算所需空间性能,可以思考如何度量
- 优化整体项目结构,(现在回看写的太chou了~)

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)