一、定义

1、FIRST集：看产生式左部

FIRST(α) = {a | α $\stackrel{\ast }{\Rightarrow }$a···，a∈$V_T$}

FIRST(α)是α的所有可能推导的开头终结符或可能的ε。

2、 FOLLOW集：看产生式右部

FOLLOW(A) = {a | S$\stackrel{\ast }{\Rightarrow }$···Aa···，a∈$V_T$}

FOLLOW(A)是所有该文法开始符推导的句型中出现在紧跟A之后的终结符或 “#”。

二、求解规则

1、FIRST集的求解规则

(1.1) 若X→a···，则将终结符 a 加入FIRST(X)中。

(1.2) 若X→ε，则将 ε 加入FIRST(X)中。

(1.3) 若X→Y…，且Y属于非终结符，则将FIRST(Y)/{ε}加入到FIRST(X)中。

(1.4) 若X→$Y_1{Y}_2\cdot \cdot \cdot Y_K$，且$Y_1,Y_2,\cdot \cdot \cdot ,Y_{i-1}$都是非终结符，且$Y_1,Y_2,\cdot \cdot \cdot ,Y_{i-1}$的FIRST集合中均包含ε，则将FIRST($Y_j$) ，(j=1,2,···,i)的所有非 ε 元素加入到FIRST(X)中，特别地，若$Y_1$~$Y_k$均有 ε 产生式，则将 ε 加到FIRST(X)中。

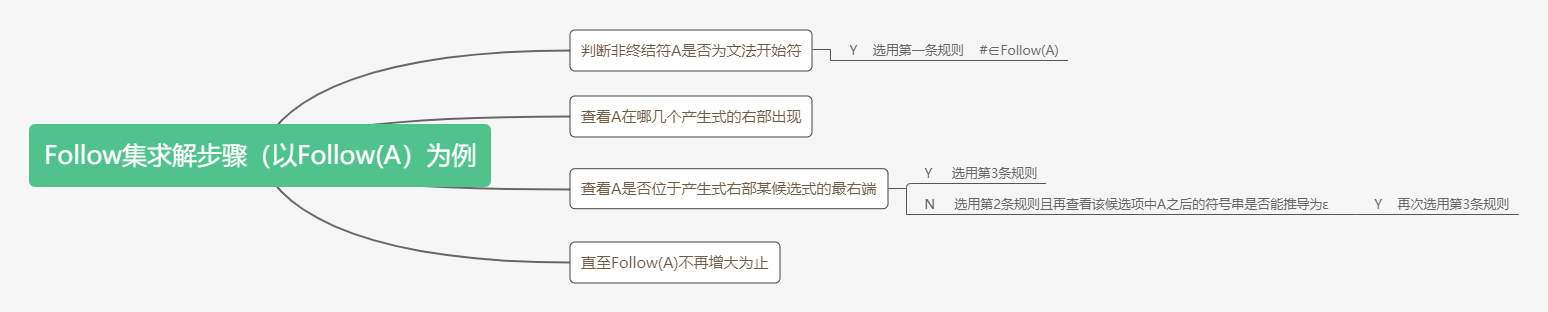
2、FOLLOW集的求解规则

(2.1) 对文法开始符号S, 置 # 于FOLLOW(S)中。

(2.2) 若有A→αBβ，则将 FIRST(β) \ {ε} 加入FOLLOW(B)中（此处 α 可以为空）。

(2.3) 若A→αB或A→αBβ,且β $\stackrel{\ast }{\Rightarrow }$ ε（即ε∈FIRST(β)），则将 FOLLOW(A)加入FOLLOW(B)中（此处 α 可以为空）。

三、求FIRST集例题

例1：写出下面文法中所有非终结符的FIRST集。

	E → TE’
	E’ → +E|ε
	T → FT’
	T’ → T|ε
	F → PF’
	F’ → *F’|ε
	P  → (E)|a|b|^

解答：

	FIRST(E’) = {+ , ε}  			规则(1.1)(1.2)
	FIRST(F’) = {* , ε}    		 	规则(1.1)(1.2)
	FIRST(P)  = {( , a , b , ^}		规则(1.1)
	FIRST(F)  = FIRST(PF’) = FIRST(P)\{ε}= {( , a , b , ^}	规则(1.3)  		FIRST(P)不包含ε
	FIRST(T)  = FIRST(FT’) = FIRST(F)\{ε}= {( , a , b , ^}	规则(1.3)  		FIRST(F)不包含ε
	FIRST(E)  = FIRST(TE’) = FIRST(T)\{ε}= {( , a , b , ^}	规则(1.3)  		FIRST(T)不包含ε
	FIRST(T’) = {FIRST(T)\{ε}} ∪ {ε} = {( , a , b , ^ ，ε}	规则(1.2)(1.3)	FIRST(T)不包含ε

例2：写出下面文法中求FIRST(S)，FIRST(A)，FIRST(B)。

	G: S → BA
	   A → BS|d
	   B → aA|bS|c

解答：

	FIRST(A) = {FIRST(B)\{ε}}∪{d} = {a, b, c, d} 
	FIRST(S) = {FIRST(B)\{ε}} = {a, b, c}
	FIRST(B)={a, b, c}

例3：写出下面文法中所有非终结符的FIRST集。

	E  → TE’
	E’ → +E|ε
	T  → Fd
	F  → PF’
	F’ → *F’|ε
	P  → (E)|a|b|ε

解答：

	FIRST(E)  = FIRST(TE’) = FIRST(T) = {( , a, b, *, d}
	FIRST(E’) = {+, ε} 
	FIRST(T)  = FIRST(Fd) 
			  = {FIRST(F)\{ε}}∪{d} 
			  = {(, a, b, *, d}
	FIRST(F)  = FIRST(PF’) 
		      = {FIRST(P)\{ε}}∪{FIRST(F’)\{ε}}∪{ε}
		      = {(, a, b, *, ε}
	FIRST(F’) = {*, ε} 
	FIRST(P)  = {(, a, b, ε}

四、求FOLLOW集例题

例1：写出下面文法中所有非终结符的FOLLOW集。

  	G:  E  → TE’
		E’ → +TE’|ε 
		T  → FT’ 
		T’ → *FT’|ε 
		F  → (E)|i

已知：

	FIRST(E)  = FIRST(T) = FIRST(F) = {(, i}
	FIRST(E’) = {+, ε}
	FIRST(T’) = {*, ε}

解答：

1、由规则(2.1)，对文法开始符E，置#于FOLLOW(E)中

	# ∈ FOLLOW(E) 

2、E在产生式F → (E)|i 的右部出现，由规则(2.2)，结合步骤1

	FOLLOW(E) = {#，)}

3、E’在产生式E → TE’和 E’ → +TE’|ε 的右部出现，由规则(2.3)

	FOLLOW(E’) = FOLLOW(E)∪FOLLOW(E’) = {#，)}

4、T在产生式 E → TE’和E’ → +TE’|ε 的右部出现，由规则(2.2)，再由规则(2.3)

	FOLLOW(T) = {FIRST(E’)\{ε}}∪FOLLOW(E)∪FOLLOW(E’) = {+，#，)}

5、T’在产生式T → FT’ 和T’ → *FT’|ε 的右部出现，由规则(2.3)

	FOLLOW(T’) = FOLLOW(T)∪FOLLOW(T’) = {+，#，)}

6、F在产生式T → FT’ 和T’ → *FT’|ε 的右部出现，由规则(2.2)，再由规则(2.3)

	FOLLOW(F) = {FIRST(T’)\{ε}}∪FOLLOW(T)∪FOLLOW(T’) = {*，+，#，)}