空洞卷积原理详解及其pytorch代码实现
空洞卷积及其pytorch实现
一、空洞卷积
1.1 普通小卷积核卷积-池化-再上采样会出现的问题
-
- Up-sampling / pooling layer (e.g. bilinear interpolation) is deterministic. (a.k.a. not learnable)内部数据结构丢失;
-
- 空间层级化信息丢失。
-
- 小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)
在这样问题的存在下,语义分割问题一直处在瓶颈期无法再明显提高精度, 而 dilated convolution 的设计就良好的避免了这些问题。
- 小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)
在图像分割领域,图像输入到CNN(典型的网络比如FCN[3])中,FCN先像传统的CNN那样对图像做卷积再pooling,降低图像尺寸的同时增大感受野,但是由于图像分割预测是pixel-wise的输出,所以要将pooling后较小的图像尺寸upsampling到原始的图像尺寸进行预测(upsampling一般采用deconv反卷积操作,deconv可参见知乎答案如何理解深度学习中的deconvolution networks?),之前的pooling操作使得每个pixel预测都能看到较大感受野信息。
因此图像分割FCN中有两个关键,一个是pooling减小图像尺寸增大感受野,另一个是upsampling扩大图像尺寸。在先减小再增大尺寸的过程中,肯定有一些信息损失掉了,那么能不能设计一种新的操作,不通过pooling也能有较大的感受野看到更多的信息呢?答案就是dilated conv。
1.2 空洞卷积的好处
空洞卷积最初的提出是为了解决图像分割的问题而提出的,常见的图像分割算法通常使用池化层和卷积层来增加感受野(Receptive Filed),同时也缩小了特征图尺寸(resolution),然后再利用上采样还原图像尺寸,特征图缩小再放大的过程造成了精度上的损失,因此需要一种操作可以在增加感受野的同时保持特征图的尺寸不变,从而代替下采样和上采样操作,在这种需求下,空洞卷积就诞生了
空洞卷积为什么能够保持特征图尺寸不变的同时增加感受野,详细原因可以参考这一篇博客:吃透空洞卷积(Dilated Convolutions)
扩大感受野:在deep net中为了增加感受野且降低计算量,总要进行降采样(pooling或s2/conv),这样虽然可以增加感受野,但空间分辨率降低了。为了能不丢失分辨率(持怀疑态度),且仍然扩大感受野,可以使用空洞卷积。这在检测,分割任务中十分有用。一方面感受野大了可以检测分割大目标,另一方面分辨率高了可以精确定位目标。捕获多尺度上下文信息:空洞卷积有一个参数可以设置dilation rate,具体含义就是在卷积核中填充dilation rate-1个0【n-1】,因此,当设置不同dilation rate时,感受野就会不一样,也即获取了多尺度信息。多尺度信息在视觉任务中相当重要。
其实说白了,就是池化可以扩大感受野,可以降低数据维度,可以减少计算量,但是会损失信息,而对于语义分割来说,这造成了发展瓶颈。而空洞卷积可以在扩大感受野的情况下不损失信息,但其实,空洞卷积的确没有损失信息,但是却没有用到所有的信息.
在二维图像上直观地感受一下扩张卷积的过程:

上图是一个扩张率为2的3×3卷积核,感受野与5×5的卷积核相同,而且仅需要9个参数。你可以把它想象成一个5×5的卷积核,每隔一行或一列删除一行或一列。
在相同的计算条件下,空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野,但计算资源有限而无法提高卷积核数量或大小时,可以考虑空洞卷积。
但是空洞卷积也有其缺点,比如连续使用的时候可能丢失局部信息等,具体可以参考空洞卷积的超详细解释
二、代码实现
空洞卷积模型定义
#pytorch封装卷积层
class ConvModule(nn.Module):
def __init__(self):
super(ConvModule,self).__init__()
#定义六层卷积层
#两层HDC(1,2,5,1,2,5)
self.conv = nn.Sequential(
#第一层 (3-1)*1+1=3 (64-3)/1 + 1 =62
nn.Conv2d(in_channels = 3,out_channels = 32,kernel_size = 3 , stride = 1,padding=0,dilation=1),
nn.BatchNorm2d(32),
# inplace-选择是否进行覆盖运算
nn.ReLU(inplace=True),
#第二层 (3-1)*2+1=5 (62-5)/1 + 1 =58
nn.Conv2d(in_channels = 32,out_channels = 32,kernel_size = 3 , stride = 1,padding=0,dilation=2),
nn.BatchNorm2d(32),
# inplace-选择是否进行覆盖运算
nn.ReLU(inplace=True),
#第三层 (3-1)*5+1=11 (58-11)/1 +1=48
nn.Conv2d(in_channels = 32,out_channels = 64,kernel_size = 3 , stride = 1,padding=0,dilation=5),
nn.BatchNorm2d(64),
# inplace-选择是否进行覆盖运算
nn.ReLU(inplace=True),
#第四层(3-1)*1+1=3 (48-3)/1 + 1 =46
nn.Conv2d(in_channels = 64,out_channels = 64,kernel_size = 3 , stride = 1,padding=0,dilation=1),
nn.BatchNorm2d(64),
# inplace-选择是否进行覆盖运算
nn.ReLU(inplace=True),
#第五层 (3-1)*2+1=5 (46-5)/1 + 1 =42
nn.Conv2d(in_channels = 64,out_channels = 64,kernel_size = 3 , stride = 1,padding=0,dilation=2),
nn.BatchNorm2d(64),
# inplace-选择是否进行覆盖运算
nn.ReLU(inplace=True),
#第六层 (3-1)*5+1=11 (42-11)/1 +1=32
nn.Conv2d(in_channels = 64,out_channels = 128,kernel_size = 3 , stride = 1,padding=0,dilation=5),
nn.BatchNorm2d(128),
# inplace-选择是否进行覆盖运算
nn.ReLU(inplace=True)
)
#输出层,将通道数变为分类数量
self.fc = nn.Linear(128,num_classes)
def forward(self,x):
#图片经过三层卷积,输出维度变为(batch_size,C_out,H,W)
out = self.conv(x)
#使用平均池化层将图片的大小变为1x1,第二个参数为最后输出的长和宽(这里默认相等了)
out = F.avg_pool2d(out,32)
#将张量out从shape batchx128x1x1 变为 batch x128
out = out.squeeze()
#输入到全连接层将输出的维度变为3
out = self.fc(out)
return out
注:可以从上面可以看出一共有6个空洞卷积层,其空洞率分别是1、2、5、1、2、5;1、2、5不包含大于1的公约数,所以其是包含2个的HDC,然后其每一层的输入和输出的算法见注释。
“3x3的kernel设置dialted-rate=2时,理应变为5x5”的kernel,多出来的空洞用0填充,这也是变相的增加了感受野。也就是说,设置dialted-rate>1时,会使得卷积的kernel变大。”
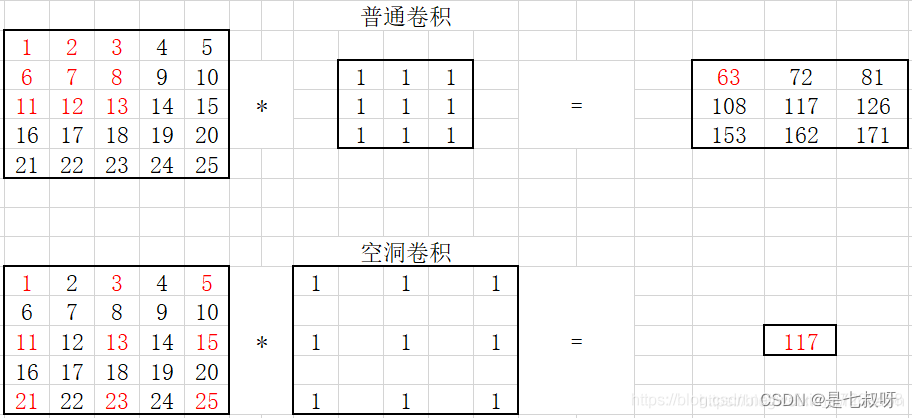
普通卷积和空洞卷积示意图:

参考文章:简书:空洞卷积(dilated convolution)理解
pytorch实现空洞卷积+残差网络实验(torch实现)
pytorch代码验证空洞卷积
【深度学习】空洞卷积(Atrous Convolution)
总结-空洞卷积(Dilated/Atrous Convolution)

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献10条内容
已为社区贡献10条内容





所有评论(0)