作者主页：爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?type=blog个人简介：打工人。

持续分享：机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。

如发现文章有误，麻烦请指出，我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666@foxmail.com 

        强化学习是一种机器学习的方法，旨在通过与环境进行交互学习来最大化累积奖励。强化学习研究的核心问题是“智能体（agent）在不断与环境交互的过程中如何选择行为以最大化奖励”。其中，A3C算法（Asynchronous Advantage Actor-Critic）是一种基于策略梯度的强化学习方法，通过多个智能体的异步训练来实现快速而稳定的学习效果。

本文将详细讲解强化学习常用算法之一“A3C”

目录

一、A3C算法的简介

二、A3C算法的发展历程

三、A3C算法的公式和原理讲解

        1. A3C算法的公式

        2. A3C算法的原理

四、A3C算法的功能

五、A3C算法的示例代码

        分解代码

        完整代码

六、总结

一、A3C算法的简介

        A3C（Asynchronous Advantage Actor-Critic）算法是一种在强化学习领域中应用广泛的算法，它结合了策略梯度方法和价值函数的学习，用于近似解决马尔可夫决策过程（Markov Decision Process）问题。A3C算法在近年来备受关注，因为它在处理大规模连续动作空间和高维状态空间方面具有出色的性能。 

二、A3C算法的发展历程

        A3C算法是对DQN（Deep Q Network）算法在强化学习领域的一个重要延伸和改进。DQN算法在2013年被DeepMind团队首次提出，并在很多任务上取得了令人瞩目的效果。然而，DQN算法在处理连续动作空间、高维状态空间等复杂问题上面临着困难。为了解决这些问题，研究人员开始关注基于策略梯度的方法，并提出了A3C算法。

三、A3C算法的公式和原理讲解

        1. A3C算法的公式

        A3C算法的目标是最大化累积奖励，将这一目标表示为优化问题，可以用如下的公式表示：

L(θ) = -E[logπ(a|s;θ)A(s,a)]

        其中，L(θ)表示损失函数，θ表示模型参数，π(a|s;θ)表示在状态s下选择动作a的概率，A(s,a)表示在状态s选择动作a相对于平均回报的优势函数。A3C算法的优化目标是最小化损失函数L(θ)。

        2. A3C算法的原理

        A3C算法采用Actor-Critic结构，由Actor和Critic两个网络组成。Actor网络的目标是学习策略函数，即在给定状态下选择动作的概率分布。Critic网络的目标是学习状态值函数或者状态-动作值函数，用于评估不同状态或状态-动作对的价值。

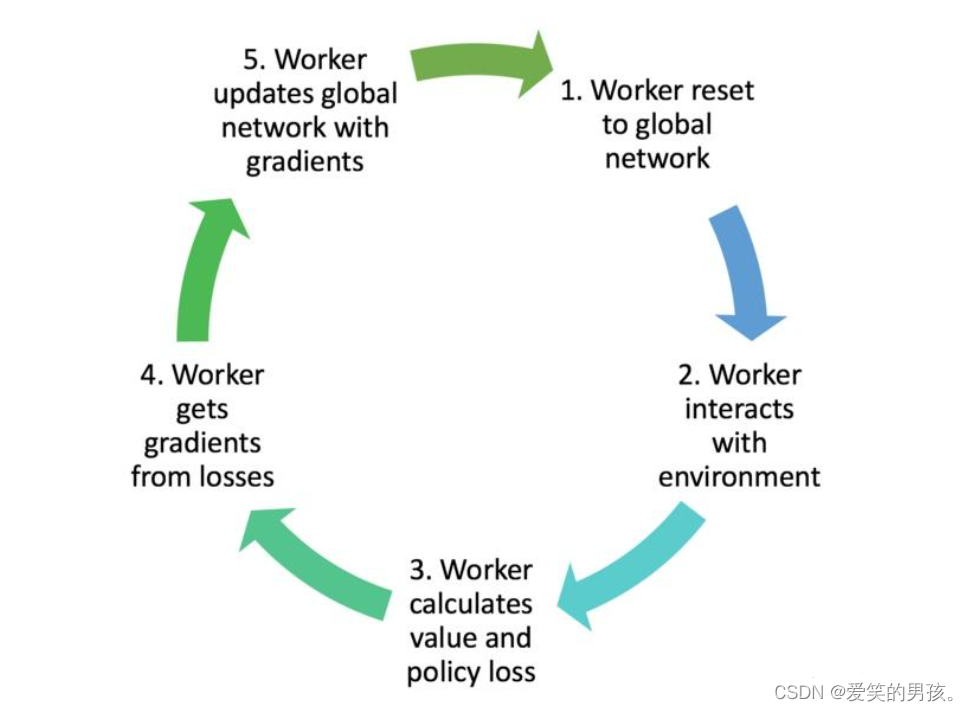
        A3C算法的训练过程可以分为以下几个步骤：

  • 初始化神经网络参数。
  • 创建多个并行的训练线程，每个线程独立运行一个智能体与环境交互，并使用Actor和Critic网络实现策略和价值的近似。
  • 每个线程根据当前的策略网络选择动作，并观测到新的状态和奖励，将这些信息存储在经验回放缓冲区中。
  • 当一个线程达到一定的时间步数或者轨迹结束时，该线程将经验回放缓冲区中的数据抽样出来，并通过计算优势函数进行梯度更新。
  • 每个线程进行一定次数的梯度更新后，将更新的参数传递给主线程进行整体参数更新。
  • 重复上述步骤直到达到预定的训练轮次或者达到终止条件为止。

        A3C算法采用了Asynchronous（异步）的训练方式，每个线程独立地与环境交互，并通过参数共享来实现梯度更新。这种异步训练的方式可以提高训练的效率和稳定性，并且能够学习到更好的策略和价值函数。

四、A3C算法的功能

        A3C算法具有以下功能和特点：

  • 支持连续动作空间和高维状态空间的强化学习；
  • 通过多个并行的智能体实现快速而稳定的训练；
  • 利用Actor和Critic两个网络分别学习策略和价值函数，具有更好的学习效果和收敛性；
  • 通过异步训练的方式提高了训练的效率和稳定性。

五、A3C算法的示例代码

        下面是一个简单的A3C算法的示例代码

        分解代码

        首先，导入需要的库和模块：

import gym
import torch
import torch.optim as optim
from torch.distributions import Categorical
import torch.multiprocessing as mp
import torch.nn as nn
import torch.nn.functional as F

        然后定义A3C算法中的Actor和Critic网络： 

class ActorCritic(nn.Module):
    def __init__(self):
        super(ActorCritic, self).__init__()
        self.fc1 = nn.Linear(4, 128)
        self.actor = nn.Linear(128, 2)
        self.critic = nn.Linear(128, 1)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        action_probs = F.softmax(self.actor(x), dim=-1)
        state_value = self.critic(x)
        return action_probs, state_value

        定义ActorCritic类来实现Actor和Critic网络的结构。

        然后定义训练函数，该函数将使用A3C算法进行智能体的训练：

def train(global_model, rank):
    env = gym.make('CartPole-v1')
    model = ActorCritic()
    model.load_state_dict(global_model.state_dict())
    optimizer = optim.Adam(global_model.parameters(), lr=0.01)
    torch.manual_seed(123 + rank)
    max_episode_length = 1000

    for episode in range(2000):
        state = env.reset()
        done = False
        episode_length = 0
        while not done and episode_length < max_episode_length:
            episode_length += 1
            state = torch.from_numpy(state).float()
            action_probs, _ = model(state)
            dist = Categorical(action_probs)
            action = dist.sample()
            next_state, reward, done, _ = env.step(action.item())

            if done:
                reward = -1

            next_state = torch.from_numpy(next_state).float()
            next_state_value = model(next_state)[-1]
            model_value = model(state)[-1]

            delta = reward + (0.99 * next_state_value * (1 - int(done))) - model_value

            actor_loss = -dist.log_prob(action) * delta.detach()
            critic_loss = delta.pow(2)

            loss = actor_loss + critic_loss

            optimizer.zero_grad()
            loss.backward()
            nn.utils.clip_grad_norm_(model.parameters(), 0.5)
            optimizer.step()

            state = next_state.numpy()

        global_model.load_state_dict(model.state_dict())

        在训练函数中，每个进程都会拷贝全局模型，并在自己的进程中进行模型的训练。训练过程中，智能体使用Actor模型根据当前状态选择动作，然后与环境进行交互，得到下一状态和奖励。根据奖励和下一状态的估值更新网络参数，得到一个损失函数。然后使用反向传播算法更新网络参数。

        最后，运行训练函数：

if __name__ == '__main__':
    num_processes = 4
    global_model = ActorCritic()
    global_model.share_memory()
    processes = []
    for rank in range(num_processes):
        p = mp.Process(target=train, args=(global_model, rank,))
        p.start()
        processes.append(p)
    for p in processes:
        p.join()

        完整代码

# -*- coding: utf-8 -*-
import gym
import torch
import torch.optim as optim
from torch.distributions import Categorical
import torch.multiprocessing as mp
import torch.nn as nn
import torch.nn.functional as F
device = torch.device("cuda")

class ActorCritic(nn.Module):
    def __init__(self):
        super(ActorCritic, self).__init__()
        self.fc1 = nn.Linear(4, 128)
        self.actor = nn.Linear(128, 2)
        self.critic = nn.Linear(128, 1)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        action_probs = F.softmax(self.actor(x), dim=-1)
        state_value = self.critic(x)
        return action_probs, state_value

def train(global_model, rank):
    env = gym.make('CartPole-v1')
    model = ActorCritic().to(device)
    model.load_state_dict(global_model.state_dict())
    optimizer = optim.Adam(global_model.parameters(), lr=0.01)
    torch.manual_seed(123 + rank)
    max_episode_length = 1000

    for episode in range(2000):
        state = env.reset()
        done = False
        episode_length = 0
        while not done and episode_length < max_episode_length:
            episode_length += 1
            state = torch.from_numpy(state).float().to(device)
            action_probs, _ = model(state)
            dist = Categorical(action_probs)
            action = dist.sample().to(device)
            next_state, reward, done, _ = env.step(action.item())

            if done:
                reward = -1

            next_state = torch.from_numpy(next_state).float().to(device)
            next_state_value = model(next_state)[-1].cpu()
            model_value = model(state)[-1].cpu()

            delta = reward + (0.99 * next_state_value * (1 - int(done))) - model_value

            actor_loss = -dist.log_prob(action) * delta.detach().to(device)
            critic_loss = delta.pow(2).to(device)

            loss = actor_loss + critic_loss

            optimizer.zero_grad()
            loss.backward()
            nn.utils.clip_grad_norm_(model.parameters(), 0.5)
            optimizer.step()

            state = next_state.cpu().numpy()

        global_model.load_state_dict(model.state_dict())

if __name__ == '__main__':
    num_processes = 4
    global_model = ActorCritic()
    global_model.share_memory()
    processes = []
    for rank in range(num_processes):
        p = mp.Process(target=train, args=(global_model, rank,))
        p.start()
        processes.append(p)
    for p in processes:
        p.join()

        因为分解代码是cpu运行...的，速度很慢，所以我在完整代码里加了cuda去运行，但是我的电脑...唉，自己看吧。。。

        上述代码使用了OpenAI Gym中的’CartPole-v1’环境作为示例，通过A3C算法训练智能体在该环境中尽可能长时间地保持杆的平衡。 

六、总结

        A3C算法是一种基于策略梯度的强化学习算法，通过多个并行的智能体异步地与环境交互，并利用Actor和Critic网络实现策略和价值的近似，从而实现快速而稳定的强化学习训练。A3C算法具有良好的学习效果和收敛性，并且适用于处理连续动作空间和高维状态空间的问题。本文讲解了A3C算法的介绍、详细讲解其发展历程、算法公式、原理、功能和示例代码，希望能让读者对A3C算法有了更加深入和全面的理解。

 

 

# 算法 # python # 人工智能
Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

“小满”安全车控操作系统正式在AtomGit开源

10月24日，由中国汽车工业协会指导，普华基础软件股份有限公司主办的“小满”安全车控操作系统开源发布会暨共建计划说明会成功举行。普华基础软件宣布将安全车控操作系统“小满”（简称“小满”）V24.10源代码正式在开放原子开源基金会（简称“基金会”）旗下AtomGit开源协作平台开源，并在AtomGit平

avatar 开放原子开发者工作坊

开放原子大赛——CIKM 2024赛果揭晓，10强争霸，角逐第33届国际信息与知识管理大会

开放原子大赛——CIKM 2024赛果揭晓，10强争霸，角逐第33届国际信息与知识管理大会

avatar 开放原子开发者工作坊

50万奖金池！开放原子大赛——第二届OpenHarmony创新应用挑战赛正式启动

50万奖金池！开放原子大赛——第二届OpenHarmony创新应用挑战赛正式启动

avatar 开放原子开发者工作坊