通俗易懂且全面的L2正则化(岭回归)解析
从多角度分析为什么正则项能够帮助防止过拟合,从而从更深层理解L2正则化(岭回归)
1. 概述
正则化的定义:减少泛化误差而不是训练误差,即避免过拟合。
L2正则化(岭回归):
目标函数
J
(
θ
)
=
1
m
∑
i
=
1
m
(
θ
T
⋅
x
(
i
)
−
y
(
i
)
)
2
+
α
∑
i
=
1
n
θ
i
2
J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(\theta^{T} \cdot x^{(i)}-y^{(i)}\right)^{2}+\alpha \sum_{i=1}^{n} \theta_{i}^{2}
J(θ)=m1i=1∑m(θT⋅x(i)−y(i))2+αi=1∑nθi2矩阵写法:
J
(
θ
)
=
(
X
θ
−
y
)
T
(
X
θ
−
y
)
+
α
1
2
∥
w
∥
2
2
J(\theta)=(\mathbf{X} \theta-\mathbf{y})^{T}(\mathbf{X} \theta-\mathbf{y})+\alpha \frac{1}{2}\|\mathbf{w}\|_{2}^{2}
J(θ)=(Xθ−y)T(Xθ−y)+α21∥w∥22
- 当 α \alpha α(乘法因子)为0时,退化为线性回归的目标函数;
- 当 α \alpha α很大时,所有权值都趋近于0。
在线性回归的基础上加入正则项 α 1 2 ∥ w ∥ 2 2 \alpha \frac{1}{2}\|\mathbf{w}\|_{2}^{2} α21∥w∥22 后,能够避免过拟合。其本质是通过权重衰减,弱化不显著的特征所占权重,下文将论证这一点。
2. 原理和分析:权重衰减
目标函数为两个正数项相加,因此在优化过程中,两个正数项都要逐渐趋近于0。可知,该正则项实际的作用是希望权重越小越好。也就是说,希望忽略一些不重要的特征。
下面先从岭回归的优化过程入手,来理解改算法是如何做到忽略不重要特征的。
下证:在岭回归训练过程中的每一步迭代都对当前的权重矩阵进行了收缩
为简单起见,忽略偏置偏置的迭代,只观察权重的迭代。此时岭回归具有以下目标函数:
J
~
(
w
;
X
,
y
)
=
α
2
w
⊤
w
+
J
(
w
;
X
,
y
)
\tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\frac{\alpha}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})
J~(w;X,y)=2αw⊤w+J(w;X,y)其中
J
J
J为线性回归的目标函数。对
w
w
w求导得到梯度为
∇
w
J
~
(
w
;
X
,
y
)
=
α
w
+
∇
w
J
(
w
;
X
,
y
)
\nabla_{\boldsymbol{w}} \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha \boldsymbol{w}+\nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})
∇wJ~(w;X,y)=αw+∇wJ(w;X,y)使用单步梯度下降更新权重
w
←
w
−
ϵ
(
α
w
+
∇
w
J
(
w
;
X
,
y
)
)
\boldsymbol{w} \leftarrow \boldsymbol{w}-\epsilon\left(\alpha \boldsymbol{w}+\nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})\right)
w←w−ϵ(αw+∇wJ(w;X,y))整理得到
w
←
(
1
−
ϵ
α
)
w
−
ϵ
∇
w
J
(
w
;
X
,
y
)
\boldsymbol{w} \leftarrow(1-\epsilon \alpha) \boldsymbol{w}-\epsilon \nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})
w←(1−ϵα)w−ϵ∇wJ(w;X,y)对比线性回归的权重迭代过程可知,岭回归的迭代过程中首先收缩了权重向量,然后再进行更新。也就是说,在每一步迭代都对当前的权重矩阵进行了收缩。
下证:在整个训练过程中,Hessian矩阵特征值越小的方向所对应权重被收缩的比例越大。
下面将分析,在整个训练过程中(即不再关注单步迭代,而是整个迭代过程),权值究竟是如何被缩放的。
先考虑线性回归的情况:
令
w
∗
\boldsymbol{w^*}
w∗未正则化的目标函数(即线性回归)取得最小训练误差时的权重向量,即
w
∗
=
arg
min
w
J
(
w
)
\boldsymbol{w}^{*}=\arg \min _{\boldsymbol{w}} J(\boldsymbol{w})
w∗=argminwJ(w),并在
w
∗
\boldsymbol{w^*}
w∗的邻域对目标函数做二次近似(泰勒级数近似),由于训练误差最小时处于极值点,函数的一阶导数为零:
J
^
(
θ
)
=
J
(
w
∗
)
+
1
2
(
w
−
w
∗
)
⊤
H
(
w
−
w
∗
)
\hat{J}(\boldsymbol{\theta})=J\left(\boldsymbol{w}^{*}\right)+\frac{1}{2}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right)^{\top} \boldsymbol{H}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right)
J^(θ)=J(w∗)+21(w−w∗)⊤H(w−w∗)其中
H
\boldsymbol{H}
H 为
J
J
J 在
w
∗
\boldsymbol{w^*}
w∗ 处计算得关于
w
\boldsymbol{w}
w 的Hessian矩阵。
其梯度为:
∇
w
J
^
(
w
)
=
H
(
w
−
w
∗
)
\nabla_{\boldsymbol{w}} \hat{J}(\boldsymbol{w})=\boldsymbol{H}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right)
∇wJ^(w)=H(w−w∗)
此处需要注意,因为
w
∗
\boldsymbol{w^*}
w∗是
J
J
J的一个最优解,可以得到
H
\boldsymbol{H}
H 是半正定的。
证明:凸函数的Hessian矩阵一定是半正定的
函数的泰勒二阶等价: f ( x ) = f ( x 0 ) + ∇ f ⊤ ( x 0 ) ( x − x 0 ) + 1 2 ( x − x 0 ) ⊤ H x 0 ( x − x 0 ) f(x)=f\left(x_{0}\right)+\nabla f^{\top}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{1}{2}\left(x-x_{0}\right)^{\top} H_{x_{0}}\left(x-x_{0}\right) f(x)=f(x0)+∇f⊤(x0)(x−x0)+21(x−x0)⊤Hx0(x−x0)
凸函数的充要条件: f ( x ) ⩾ f ( x 0 ) + ∇ f ⊤ ( x 0 ) ( x − x 0 ) f(x) \geqslant f\left(x_{0}\right)+\nabla f^{\top}\left(x_{0}\right)\left(x-x_{0}\right) f(x)⩾f(x0)+∇f⊤(x0)(x−x0)
因此 f ( x ) = f ( x 0 ) + ∇ f ⊤ ( x 0 ) ( x − x 0 ) + 1 2 ( x − x 0 ) ⊤ H x 0 ( x − x 0 ) ⩾ f ( x 0 ) + ∇ f ⊤ ( x 0 ) ( x − x 0 ) f(x)=f\left(x_{0}\right)+\nabla f^{\top}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{1}{2}\left(x-x_{0}\right)^{\top} H_{x_{0}}\left(x-x_{0}\right)\geqslant f\left(x_{0}\right)+\nabla f^{\top}\left(x_{0}\right)\left(x-x_{0}\right) f(x)=f(x0)+∇f⊤(x0)(x−x0)+21(x−x0)⊤Hx0(x−x0)⩾f(x0)+∇f⊤(x0)(x−x0)
即 1 2 ( x − x 0 ) ⊤ H x 0 ( x − x 0 ) ⩾ 0 \frac{1}{2}\left(x-x_{0}\right)^{\top} H_{x_{0}}\left(x-x_{0}\right) \geqslant 0 21(x−x0)⊤Hx0(x−x0)⩾0
也就是矩阵 H H H满足半正定矩阵定义。
再分析岭回归的情况:
上面已经求得岭回归的梯度为
∇
w
J
~
(
w
;
X
,
y
)
=
α
w
+
∇
w
J
(
w
;
X
,
y
)
\nabla_{\boldsymbol{w}} \tilde{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=\alpha \boldsymbol{w}+\nabla_{\boldsymbol{w}} J(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})
∇wJ~(w;X,y)=αw+∇wJ(w;X,y)使用变量
w
~
\tilde{w}
w~ 表示岭回归的最优点,和之前求得的
∇
w
J
^
(
w
)
=
H
(
w
−
w
∗
)
\nabla_{\boldsymbol{w}} \hat{J}(\boldsymbol{w})=\boldsymbol{H}\left(\boldsymbol{w}-\boldsymbol{w}^{*}\right)
∇wJ^(w)=H(w−w∗)代入上述梯度公式,且最优点的梯度为0,得
α
w
ˉ
+
H
(
w
~
−
w
∗
)
=
0
\alpha \bar{\boldsymbol{w}}+\boldsymbol{H}\left(\tilde{w}-w^{*}\right)=0
αwˉ+H(w~−w∗)=0解得
w
~
=
(
H
+
α
I
)
−
1
H
w
∗
\tilde{w}=(\boldsymbol{H}+\alpha \boldsymbol{I})^{-1} \boldsymbol{H} w^{*}
w~=(H+αI)−1Hw∗因为
H
\boldsymbol{H}
H 是半正定的,所以
H
\boldsymbol{H}
H 是实对称的,因此可以使用特征分解(谱分解),将其分解为一个对角矩阵
Λ
\Lambda
Λ 和一组特征向量的标准正交基
Q
Q
Q,即
H
=
Q
Λ
Q
⊤
H=Q \Lambda Q^{\top}
H=QΛQ⊤,将其带入上式得到
w
~
=
(
Q
Λ
Q
⊤
+
α
I
)
−
1
Q
Λ
Q
⊤
w
∗
=
[
Q
(
Λ
+
α
I
)
Q
⊤
]
−
1
Q
Λ
Q
⊤
w
∗
=
Q
(
Λ
+
α
I
)
−
1
Λ
Q
⊤
w
∗
\begin{aligned} \tilde{w} &=\left(\boldsymbol{Q} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top}+\alpha \boldsymbol{I}\right)^{-1} \boldsymbol{Q} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \\ &=\left[\boldsymbol{Q}(\boldsymbol{\Lambda}+\alpha \boldsymbol{I}) \boldsymbol{Q}^{\top}\right]^{-1} \boldsymbol{Q} \boldsymbol{\Lambda} Q^{\top} w^{*} \\ &=\boldsymbol{Q}(\boldsymbol{\Lambda}+\alpha \boldsymbol{I})^{-1} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \end{aligned}
w~=(QΛQ⊤+αI)−1QΛQ⊤w∗=[Q(Λ+αI)Q⊤]−1QΛQ⊤w∗=Q(Λ+αI)−1ΛQ⊤w∗可以得出结论:权重衰减的效果是沿着由
H
\boldsymbol{H}
H 的特征向量所定义的轴缩放
w
∗
\boldsymbol{w}^{*}
w∗,根据
λ
i
λ
i
+
α
\frac{\lambda_{i}}{\lambda_{i}+\alpha}
λi+αλi 因子缩放与
H
\boldsymbol{H}
H 第
i
i
i 个特征向量对齐的
w
∗
\boldsymbol{w}^{*}
w∗ 的分量。沿着
H
\boldsymbol{H}
H 特征值较大的方向 (如
λ
i
≫
a
\lambda_{i} \gg a
λi≫a)正则化的影响较小。而
λ
i
≪
a
\lambda_{i} \ll a
λi≪a 的分量将会收缩到几乎为零。
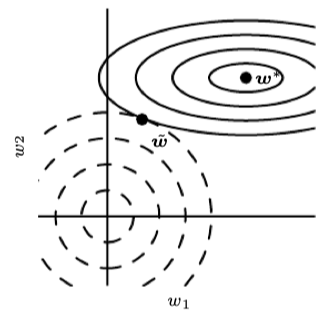
从几何角度理解这种效应:帮助算法往收益最大的方向下降,尽力忽视收益小的方向。

上图中,实线椭圆为不加正则项的目标函数(线性回归)等值线,虚线圆圈表示 L2 正则化项的等值线。目标函数
J
J
J 在第一维的变化速度很小,等值线稀疏,Hessian矩阵的第一特征值小,因此当
w
∗
\boldsymbol{w}^{*}
w∗ 水平移动时,目标函数不会变化太多,因为目标函数对这个方向没有强烈的偏好,所以正则化项对该轴具有强烈的影响;相反,目标函数
J
J
J 在第二维的变化速度很大,等值线密集,Hessian矩阵的第二特征值大,因此当
w
∗
\boldsymbol{w}^{*}
w∗ 竖直移动时,目标函数会更快速的变化,权重衰减对
w
2
w_2
w2 的位置影响相对较小。
只有在显著减小目标函数方向上的参数会保留得相对完好。在无助于目标函数减小的方向(对应 Hessian 矩阵较小的特征值)上改变参数不会显著增加梯度。这种不重要方向对应的分量会在训练过程中因正则化而衰减掉。 防止算法在无必要的方向上下降,即防止了过拟合。
从机器学习的角度理解这种效应:方差越小的特征(包含信息量越小的特征)所对应的权重缩减越大。
以分类任务为例,当特征的方差为0时,不管该样本属于什么类别,他们都拥有相同的值,即该特征无法帮助分类,因此可以认为方差越小的特征所含有的信息量越少。如果拘泥于含有信息量很少的特征,则容易发生过拟合。比如,我们需要分类咖啡和巧克力,用于训练的样本中咖啡的颜色相比巧克力几乎相同(样本特征方差不大),如果我们以这个特征分类,即认为深色一些的都是咖啡,当真实样本中出现牛奶咖啡,算法就会将其误分类为巧克力,即发生了过拟合。下面将从机器学习的角度,来揭示该算法是如何帮助忽视信息量小的特征以实现防止过拟合的:
线性回归的代价函数是平方误差之和:
(
X
w
−
y
)
⊤
(
X
w
−
y
)
(\boldsymbol{X} \boldsymbol{w}-\boldsymbol{y})^{\top}(\boldsymbol{X} \boldsymbol{w}-\boldsymbol{y})
(Xw−y)⊤(Xw−y)添加正则项后,代价函数变为:
(
X
w
−
y
)
⊤
(
X
w
−
y
)
+
1
2
α
w
⊤
w
(\boldsymbol{X} \boldsymbol{w}-\boldsymbol{y})^{\top}(\boldsymbol{X} \boldsymbol{w}-\boldsymbol{y})+\frac{1}{2} \alpha \boldsymbol{w}^{\top} \boldsymbol{w}
(Xw−y)⊤(Xw−y)+21αw⊤w当代价函数在理想情况下被优化为0时,线性回归的解为:
w
=
(
X
⊤
X
)
−
1
X
⊤
y
\boldsymbol{w}=\left(\boldsymbol{X}^{\top} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\top} \boldsymbol{y}
w=(X⊤X)−1X⊤y而正则后的解为
w
=
(
X
⊤
X
+
α
I
)
−
1
X
⊤
y
\boldsymbol{w}=\left(\boldsymbol{X}^{\top} \boldsymbol{X}+\alpha \boldsymbol{I}\right)^{-1}\boldsymbol{X}^{\top} \boldsymbol{y}
w=(X⊤X+αI)−1X⊤y
式中
X
⊤
X
\boldsymbol{X}^{\top} \boldsymbol{X}
X⊤X与协方差矩阵
1
m
X
⊤
X
\frac{1}{m} \boldsymbol{X}^{\top} \boldsymbol{X}
m1X⊤X成正比(通常会对数据进行正则化处理,可以认为数据都进行了demean操作,如果没有进行正则化,这里就变成二范数越小影响越大),L2 正则项将这个矩阵替换为
(
X
⊤
X
+
α
I
)
−
1
\left(\boldsymbol{X}^{\top} \boldsymbol{X}+\alpha \boldsymbol{I}\right)^{-1}
(X⊤X+αI)−1。这个矩阵的对角项对应每个输入特征的方差,也就是说方差越大,受到的影响越小。L2正则化能 让学习算法 ‘‘感知’’ 到具有较高方差的输入
x
\boldsymbol{x}
x,因此信息量较少的特征的权重将会收缩。
与PCA的联系:
PCA同样通过协方差矩阵的特征值分解,将较小的特征值直接置零,即也是缩减了方差较小的特征的权重,从而忽略了含有信息量少的特征。
参考文献
Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016.

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)