GA-BP神经网络——遗传算法优化BP神经网络Python实现

使用遗传算法（GA）优化BP神经网络。

x_8efengfan

8904人浏览 · 2024-03-06 00:19:16

x_8efengfan · 2024-03-06 00:19:16 发布

文章目录

前言
一、遗传算法优化BP神经网络
二、代码实现
三、程序测试
- 3.1 问题描述与测试代码
- 3.2 测试结果
四、完整代码

前言

善始者繁多，克终者盖寡。

先来回顾一下BP（Back Propagation）神经网络和遗传算法（Genetic Algorithm，GA）。
神经网络算法模仿了生理学上的神经网络，主要通过反向传播不断调整权重和偏置以减小误差（此时的误差就是损失函数），从而获取更准确的预测结果，在处理非线性问题和不确定性问题时具有良好的泛化能力，但是模型中初始参数会严重影响模型的性能，某些时候得到的结果往往不是全局最优。BP神经网络实例请看往期文章numpy手写BP神经网络。

遗传算法以达尔文进化理论为基础，是模拟生物进化过程以获取问题最优解的算法，涉及的操作主要有选择、交叉（繁衍）、变异，重要的概念有编码、个体、种群、适合度。该算法中通过选择操作挑选出优秀的个体，被选中的可能是依赖于个体适合度的高低，适合度高的个体被选中的可能性更大；通过交叉操作生成新的个体；通过变异操作扩大样本空间，增加随机性。遗传算法实例请看往期文章GA遗传算法。

一、遗传算法优化BP神经网络

1. 将神经网络中所有的权重、偏置组合为种群中的一个个体；
2. 将神经网络的实际输出与真实值间的误差作为GA的适合度函数；
3. 使用“优胜劣汰”替换BP神经网络中的反向传播过程；
4. 繁衍n代，从种群中挑选适合度最高的个体（个体就是权重和偏置的组合），相当于模型已经训练完毕，该个体就是模型最优时权重、偏置的值。

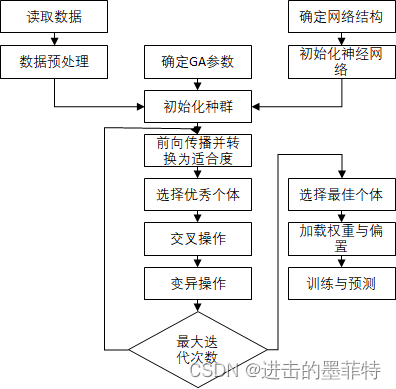
图解GA-BP神经网络：

在这里插入图片描述

请注意，此时种群中“个体”就是权重和偏置的连接形成的，在选择、交叉、变异操作中均有权重和偏置的更新操作！！！与BP神经网络中的反向传播对应，可以简单的理解为将反向传播操作替换为选择、交叉、变化操作。

二、代码实现

2.1 确定网络结构和GA参数

类中涉及BP神经网络的参数有num_inputs、num_hidden、num_outputs、learning_rate，分别表示神经网络的输入层、隐含层、输出层神经元个数以及神经网络的学习率。
涉及GA的参数有population 、population_size、fitness_values、mutation_rate ，分布表示种群本身、种群大小、种群中个体适合度的集合、变异概率。
此处种群优秀个体的依据是个体的适合度，所以后续会涉及大量的随机取值操作，于是在类中内置一个随机数生成器。

    def __init__(self, num_inputs, num_hidden, num_outputs, population_size, mutation_rate, learning_rate):
        self.num_inputs = num_inputs
        self.num_hidden = num_hidden
        self.num_outputs = num_outputs
        self.learning_rate = learning_rate

        self.population = []
        self.population_size = population_size
        #通过变异操作能够增大样本输入空间，类似于学习率，此处也以参数形式传入
        self.mutation_rate = mutation_rate
        #种群中各个体的适合度，fitness_values的大小与种群中个体数相同
        self.fitness_values = np.zeros(population_size)
        #后续操作中需要频繁使用随机取数的操作，所有在类中内置一个随机数生成器
        self.random_state = check_random_state(None)  # 设置随机数种子

2.2 初始化神经网络和种群

神经网络的初始参数通过numpy随机生成，此网络结构仅包含一个隐含层，所有权重只有input_hidden_weights、hidden_output_weights两个二维矩阵，将两个权重作为一个整体（通过元组的方式实现，因为相较于列表，元组内容不可变）加入种群中。
注意：虽然该网络结构只有两个权重，但实际运行时模型参数体量也是极其巨大的，受限于硬件条件，此处未添加偏置！！！

    #初始化种群，也是初始化神经网络权重的过程，将某次随机生成的权重当做种群中的一个对象
    def initialize_population(self):
        # 短横杠表示临时参数，和占位符一个作用
        for _ in range(self.population_size):
            input_hidden_weights = np.random.uniform(low=-1, high=1, size=(self.num_inputs, self.num_hidden))
            hidden_output_weights = np.random.uniform(low=-1, high=1, size=(self.num_hidden, self.num_outputs))
            self.population.append((input_hidden_weights, hidden_output_weights))

2.3 前向传播并转换为适合度

种群中每一个个体都表示一组权重的组合，也就是一种方案，我们期望从中找出一种让模型效果最佳的方案，而判断某个方案优劣的依据是模型输出与真实数据间的误差，所以我们得先计算出每一种方案下模型的误差（这里用方差表示），该过程对应BP神经网络的前向传播过程。
某方案下模型的误差越小，说明该方案越好，放在种群中来说就是该个体适合度越高，我们很容易联想到用误差的倒数来表示种群中个体的适合度。

    #适合度函数
    def evaluate_fitness(self, x, y):
        #计算中权重每个对象（权重）的适合度，并将适合度保存到fitness_values中
        for i in range(self.population_size):
            #此处为前向传播，计算中间层和输出层的激活值
            input_hidden_weights, hidden_output_weights = self.population[i]
            hidden_activations = self.sigmoid(np.dot(x, input_hidden_weights))
            output_activations  = np.dot(hidden_activations, hidden_output_weights)
            #以方差作为损失函数，将损失函数的倒数作为适合度，损失函数越小，适合度函数值越大
            error = np.mean((output_activations - y) ** 2)
            self.fitness_values[i] = 1 / (error + 1e-8)

2.4 选择优秀个体

种群中所有个体的适合度计算出来后，我们就要挑选出优秀的个体以进行后续的繁衍行为，某个体被选择的几率取决于其适合度的高低，适合度高则被选择的几率大，此处用“个体适合度/总体适合度”表示某个体被选中的概率。

注意：有种观点是将个体按照适合度的高低进行排序，重复选择适合度较高的几个个体，本人对该观点存疑。
假设种群中有100个个体，在选择优秀个体时只重复选择适合度前10的个体组成新的种群，现适合度排名第十的个体A适合度为0.08，排名第十一的个体B适合度为0.79998，两者适合度相差无几，说不定经过变异操作B的适合度会高于个体A。
所有本人更倾向于用概率的方法来选择优秀个体。

    def selection(self):
        #计算总适合度，并将适合度转换为被选中的概率
        total_fitness = np.sum(self.fitness_values)
        selection_probs = self.fitness_values / total_fitness
        #从种群中随机选择一些对象（依据概率），并将其保存到selected_population中
        selected_indices = self.random_state.choice(np.arange(self.population_size), size=self.population_size, replace=True, p=selection_probs)
        selected_population = []
        for idx in selected_indices:
            selected_population.append(self.population[idx])

        self.population = selected_population

2.5 交叉操作

交叉操作是种群繁衍的主要操作，其思路是随机从种群中挑选两个个体，交换其部分信息以生成新的个体。而且，我们有理由让优秀的个体繁衍的可能性更大！！！
交叉操作二进制形式演示可参看GA遗传算法对应章节。

从代码角度看，具体操作是：

计算种群中各个体适合度；
使用类中随机数生成器选择父、母个体的下标，使用“p=selection_probs ”指定个体被选中的概率；
随机指定父、母个体交叉位置（此处个体表示的是input_hidden_weights、hidden_output_weights形成的元组，元组交叉类似于字符串拼接），生成新的个体；
用新的种群替换原来的种群。

    #交叉（繁衍行为的主要操作）
    def crossover(self):
        offspring_population = []
        # 计算总适合度，并将适合度转换为被选中的概率，因为我们有理由让适合度高的个体参与到繁衍的过程中
        total_fitness = np.sum(self.fitness_values)
        selection_probs = self.fitness_values / total_fitness

        for _ in range(self.population_size):
            #parent是input_hidden_weights、hidden_output_weights组合而成的元组
            parent1_indices = self.random_state.choice(np.arange(self.population_size),p=selection_probs)
            parent2_indices = self.random_state.choice(np.arange(self.population_size),p=selection_probs)
            input_hidden_weights1, hidden_output_weights1 = self.population[parent1_indices]
            input_hidden_weights2, hidden_output_weights2 = self.population[parent2_indices]
            #对w1进行交叉操作，交叉点随机（把input1前半部分和Input2后半部分拼接）
            crossover_point = self.random_state.randint(0, self.num_hidden)
            input_hidden_weights = np.concatenate((input_hidden_weights1[:, :crossover_point], input_hidden_weights2[:, crossover_point:]), axis=1)
            #对w2进行交叉操作，交叉点随机
            crossover_point = self.random_state.randint(0, self.num_outputs)
            hidden_output_weights = np.concatenate((hidden_output_weights1[:, :crossover_point], hidden_output_weights2[:, crossover_point:]), axis=1)
            #将繁衍产生的对象放入新的种群，直至生成population_size个对象
            offspring_population.append((input_hidden_weights, hidden_output_weights))

        self.population = offspring_population

2.6 变异操作

变异操作增大了样本的输入空间，变异概率不宜过大，通常为1%~10%。具体代码实现就是在原有权重上整体添加一个较小的值，达到数据变化的效果。
此处变异操作与GA遗传算法中的具体实现有所不同。

    #变异
    def mutation(self):
        for i in range(self.population_size):
            input_hidden_weights, hidden_output_weights = self.population[i]

            if self.random_state.rand() < self.mutation_rate:
                input_hidden_weights += np.random.uniform(low=-0.1, high=0.1, size=(self.num_inputs, self.num_hidden))

            if self.random_state.rand() < self.mutation_rate:
                hidden_output_weights += np.random.uniform(low=-0.1, high=0.1, size=(self.num_hidden, self.num_outputs))

            self.population[i] = (input_hidden_weights, hidden_output_weights)

2.7 训练模型

在BP神经网络中，理想情况是经过训练后的神经网络模型效果最佳，也就是经过训练后的神经网络模型权重、偏置等参数达到最优。
同样，GA-BP神经网络经过num_generations代繁衍后其输出也应当是所有个体中的最优个体，也可以说是所有方案中的最优方案，即最佳的input_hidden_weights和hidden_output_weights。

    def train(self, x, y, num_generations):
        self.initialize_population()

        for generation in range(num_generations):
            self.evaluate_fitness(x, y)
            self.selection()
            #挑选出优秀个体后重新计算种群中个体适合度，因为我们有理由让适合度高的个体参与到繁衍的过程中
            self.evaluate_fitness(x, y)
            self.crossover()
            self.mutation()

        best_weights = self.population[np.argmax(self.fitness_values)]
        input_hidden_weights, hidden_output_weights = best_weights

        return input_hidden_weights, hidden_output_weights

三、程序测试

3.1 问题描述与测试代码

使用GA-BP神经网络模型“异或”操作，测试程序中将模型保存为“.npy”格式的文件，目的是加快程序运行速度。
测试程序中创建了“2101”的网络结构，包含30个权重参数，种群中包含100个个体，繁衍一次需要更新30*100个参数，程序中共繁衍10000代，除去变异等操作，至少需要执行30 * 100 * 10000次操作，当神经网络神经元个数、网络层数、繁衍代数增加时，计算次数会更多。

if __name__ == '__main__':
    # 设置神经网络和遗传算法参数
    num_inputs = 2
    num_hidden = 10
    num_outputs = 1
    population_size = 100
    mutation_rate = 0.01
    learning_rate = 0.1
    num_generations = 10000

    # 创建GA-BP神经网络对象
    ga_bp = GeneticAlgorithmBP(num_inputs, num_hidden, num_outputs, population_size, mutation_rate, learning_rate)

    # 创建训练数据集
    x_train = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    y_train = np.array([[0], [1], [1], [0]])

    #读取input_hidden_weights.npy文件
    if os.path.exists('input_hidden_weights.npy'):
        # 读取权重文件
        input_hidden_weights = np.load('input_hidden_weights.npy')
        hidden_output_weights = np.load('hidden_output_weights.npy')
    else:
        # 训练神经网络
        input_hidden_weights, hidden_output_weights = ga_bp.train(x_train, y_train, num_generations)
        #保存权重
        np.save('input_hidden_weights.npy', input_hidden_weights)
        np.save('hidden_output_weights.npy', hidden_output_weights)

    # 使用训练好的权重进行预测
    hidden_activations = ga_bp.sigmoid(np.dot(x_train, input_hidden_weights))
    output_activations  = np.dot(hidden_activations, hidden_output_weights)
    # predictions = np.round(output_activations)
    predictions = output_activations
    print("预测结果：")
    print(predictions)

3.2 测试结果

预测误差较小，已经十分接近真实结果了。
在这里插入图片描述

四、完整代码

import numpy as np
from sklearn.utils import check_random_state

import os


class GeneticAlgorithmBP:
    def __init__(self, num_inputs, num_hidden, num_outputs, population_size, mutation_rate, learning_rate):
        self.num_inputs = num_inputs
        self.num_hidden = num_hidden
        self.num_outputs = num_outputs
        self.learning_rate = learning_rate

        self.population = []
        self.population_size = population_size
        #通过变异操作能够增大样本输入空间，类似于学习率，此处也以参数形式传入
        self.mutation_rate = mutation_rate
        #种群中各个体的适合度，fitness_values的大小与种群中个体数相同
        self.fitness_values = np.zeros(population_size)
        #后续操作中需要频繁使用随机取数的操作，所有在类中内置一个随机数生成器
        self.random_state = check_random_state(None)  # 设置随机数种子

    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    #初始化种群，也是初始化神经网络权重的过程，将某次随机生成的权重当做种群中的一个对象
    def initialize_population(self):
        # 短横杠表示临时参数，和占位符一个作用
        for _ in range(self.population_size):
            input_hidden_weights = np.random.uniform(low=-1, high=1, size=(self.num_inputs, self.num_hidden))
            hidden_output_weights = np.random.uniform(low=-1, high=1, size=(self.num_hidden, self.num_outputs))
            self.population.append((input_hidden_weights, hidden_output_weights))

    #适合度函数
    def evaluate_fitness(self, x, y):
        #计算中权重每个对象（权重）的适合度，并将适合度保存到fitness_values中
        for i in range(self.population_size):
            #此处为前向传播，计算中间层和输出层的激活值
            input_hidden_weights, hidden_output_weights = self.population[i]
            hidden_activations = self.sigmoid(np.dot(x, input_hidden_weights))
            output_activations  = np.dot(hidden_activations, hidden_output_weights)
            #以方差作为损失函数，将损失函数的倒数作为适合度，损失函数越小，适合度函数值越大
            error = np.mean((output_activations - y) ** 2)
            self.fitness_values[i] = 1 / (error + 1e-8)

    def selection(self):
        #计算总适合度，并将适合度转换为被选中的概率
        total_fitness = np.sum(self.fitness_values)
        selection_probs = self.fitness_values / total_fitness
        #从种群中随机选择一些对象（依据概率），并将其保存到selected_population中
        selected_indices = self.random_state.choice(np.arange(self.population_size), size=self.population_size, replace=True, p=selection_probs)
        selected_population = []
        for idx in selected_indices:
            selected_population.append(self.population[idx])

        self.population = selected_population

    #交叉（繁衍行为的主要操作）
    def crossover(self):
        offspring_population = []
        # 计算总适合度，并将适合度转换为被选中的概率，因为我们有理由让适合度高的个体参与到繁衍的过程中
        total_fitness = np.sum(self.fitness_values)
        selection_probs = self.fitness_values / total_fitness

        for _ in range(self.population_size):
            #parent是input_hidden_weights、hidden_output_weights组合而成的元组
            parent1_indices = self.random_state.choice(np.arange(self.population_size),p=selection_probs)
            parent2_indices = self.random_state.choice(np.arange(self.population_size),p=selection_probs)
            input_hidden_weights1, hidden_output_weights1 = self.population[parent1_indices]
            input_hidden_weights2, hidden_output_weights2 = self.population[parent2_indices]
            #对w1进行交叉操作，交叉点随机（把input1前半部分和Input2后半部分拼接）
            crossover_point = self.random_state.randint(0, self.num_hidden)
            input_hidden_weights = np.concatenate((input_hidden_weights1[:, :crossover_point], input_hidden_weights2[:, crossover_point:]), axis=1)
            #对w2进行交叉操作，交叉点随机
            crossover_point = self.random_state.randint(0, self.num_outputs)
            hidden_output_weights = np.concatenate((hidden_output_weights1[:, :crossover_point], hidden_output_weights2[:, crossover_point:]), axis=1)
            #将繁衍产生的对象放入新的种群，直至生成population_size个对象
            offspring_population.append((input_hidden_weights, hidden_output_weights))

        self.population = offspring_population

    #变异
    def mutation(self):
        for i in range(self.population_size):
            input_hidden_weights, hidden_output_weights = self.population[i]

            if self.random_state.rand() < self.mutation_rate:
                input_hidden_weights += np.random.uniform(low=-0.1, high=0.1, size=(self.num_inputs, self.num_hidden))

            if self.random_state.rand() < self.mutation_rate:
                hidden_output_weights += np.random.uniform(low=-0.1, high=0.1, size=(self.num_hidden, self.num_outputs))

            self.population[i] = (input_hidden_weights, hidden_output_weights)

    def train(self, x, y, num_generations):
        self.initialize_population()

        for generation in range(num_generations):
            self.evaluate_fitness(x, y)
            self.selection()
            #挑选出优秀个体后重新计算种群中个体适合度，因为我们有理由让适合度高的个体参与到繁衍的过程中
            self.evaluate_fitness(x, y)
            self.crossover()
            self.mutation()

        best_weights = self.population[np.argmax(self.fitness_values)]
        input_hidden_weights, hidden_output_weights = best_weights

        return input_hidden_weights, hidden_output_weights

if __name__ == '__main__':
    # 设置神经网络和遗传算法参数
    num_inputs = 2
    num_hidden = 10
    num_outputs = 1
    population_size = 100
    mutation_rate = 0.01
    learning_rate = 0.1
    num_generations = 10000

    # 创建GA-BP神经网络对象
    ga_bp = GeneticAlgorithmBP(num_inputs, num_hidden, num_outputs, population_size, mutation_rate, learning_rate)

    # 创建训练数据集
    x_train = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    y_train = np.array([[0], [1], [1], [0]])

    #读取input_hidden_weights.npy文件
    if os.path.exists('input_hidden_weights.npy'):
        # 读取权重文件
        input_hidden_weights = np.load('input_hidden_weights.npy')
        hidden_output_weights = np.load('hidden_output_weights.npy')
    else:
        # 训练神经网络
        input_hidden_weights, hidden_output_weights = ga_bp.train(x_train, y_train, num_generations)
        #保存权重
        np.save('input_hidden_weights.npy', input_hidden_weights)
        np.save('hidden_output_weights.npy', hidden_output_weights)

    # 使用训练好的权重进行预测
    hidden_activations = ga_bp.sigmoid(np.dot(x_train, input_hidden_weights))
    output_activations  = np.dot(hidden_activations, hidden_output_weights)
    # predictions = np.round(output_activations)
    predictions = output_activations
    print("预测结果：")
    print(predictions)