线结构光三维重建（一）icon-default.png?t=M85Bhttps://blog.csdn.net/beyond951/article/details/125771158        

        上文主要对线激光的三角测量原理、光平面的标定方法和激光条纹提取的方法进行了一个简单的介绍，本文则主要针对线激光三维重建系统的系统参数标定进行阐述，同时对采集到的图片进行标定。本文主要涉及到的几个重难点：相机标定、激光条纹提取、光平面的标定和坐标系变换的理解。

相机标定

        本博客有多篇文章详细阐述了相机标定的理论推导过程，可详细参考下面链接文章的推导和实现。

北邮鲁鹏老师三维重建课程之相机标定icon-default.png?t=M85Bhttps://blog.csdn.net/beyond951/article/details/122201757?spm=1001.2014.3001.5501相机标定-机器视觉基础（理论推导、Halcon和OpenCV相机标定）icon-default.png?t=M85Bhttps://blog.csdn.net/beyond951/article/details/126435661?spm=1001.2014.3001.5502        

        最后标定的结果如下，标定过程中寻找棋盘格角点的检测图、标定的相机内参、经过内参矫正的图片和对应标定板生成的外参。

 

激光条纹提取

        本文采用激光条纹提取方式有灰度重心法和Steger算法，对激光条纹的中心点进行提取。

灰度重心法

vector<Point2f> GetLinePointsGrayWeight(Mat& src, int gray_Thed, int Min, int Max, int Type)
{
	vector<Point2f> points_vec;
	if (Type == 0)
	{
		Min = Min < 0 ? 0 : Min;
		Max = Max > src.rows ? src.rows : Max;
		for (int i = 0; i < src.cols; i++)
		{
			float X0 = 0, Y0 = 0;
			for (int j = Min; j < Max; j++)
			{
				if (src.at<ushort>(j, i) > gray_Thed)
				{
					X0 += src.at<ushort>(j, i) * j;
					Y0 += src.at<ushort>(j, i);
				}
			}
			if (Y0 != 0)
			{
				//Point p = Point(i, X0 / Y0);
				points_vec.push_back(Point2f(i, X0 / (float)Y0));
			}
			else
			{
				//points_vec.push_back(Point2f(i, -1));
			}
		}
	}
	else
	{
		Min = Min < 0 ? 0 : Min;
		Max = Max > src.cols ? src.cols : Max;
		for (int i = 0; i < src.rows; i++)
		{
			int X0 = 0, Y0 = 0;
			for (int j = Min; j < Max; j++)
			{
				if (src.at<Vec3b>(i, j)[0] > gray_Thed)
				{
					X0 += src.at<Vec3b>(i, j)[0] * j;
					Y0 += src.at<Vec3b>(i, j)[0];
				}
			}
			if (Y0 != 0)
			{
				points_vec.push_back(Point2f(X0 / (float)Y0, i));
			}
			else
			{
				points_vec.push_back(Point2f(-1, i));
			}
		}
	}
	return points_vec;
}

Steger算法

vector<Point2f> GetLinePoints_Steger(Mat& src, int gray_Thed, int Min, int Max, int Type)
{
	Mat srcGray, srcGray1;
	cvtColor(src, srcGray1, CV_BGR2GRAY);

	//高斯滤波
	srcGray = srcGray1.clone();
	srcGray.convertTo(srcGray, CV_32FC1);
	GaussianBlur(srcGray, srcGray, Size(0, 0), 6, 6);


	//一阶偏导数
	Mat m1, m2;
	m1 = (Mat_<float>(1, 2) << 1, -1);//x方向的偏导数
	m2 = (Mat_<float>(2, 1) << 1, -1);//y方向的偏导数
	Mat dx, dy;
	filter2D(srcGray, dx, CV_32FC1, m1);
	filter2D(srcGray, dy, CV_32FC1, m2);
	//二阶偏导数
	Mat m3, m4, m5;
	m3 = (Mat_<float>(1, 3) << 1, -2, 1);   //二阶x偏导
	m4 = (Mat_<float>(3, 1) << 1, -2, 1);   //二阶y偏导
	m5 = (Mat_<float>(2, 2) << 1, -1, -1, 1);   //二阶xy偏导
	Mat dxx, dyy, dxy;
	filter2D(srcGray, dxx, CV_32FC1, m3);
	filter2D(srcGray, dyy, CV_32FC1, m4);
	filter2D(srcGray, dxy, CV_32FC1, m5);
	//hessian矩阵
	double maxD = -1;
	vector<double> Pt;
	vector<Point2f> points_vec;
	if (Type == 0)
	{
		Min = Min < 0 ? 0 : Min;
		Max = Max > src.rows ? src.rows : Max;
		for (int i = 0; i < src.cols; i++)
		{
			for (int j = Min; j < Max; j++)
			{
				if (srcGray.at<uchar>(j, i) > gray_Thed)
				{
					Mat hessian(2, 2, CV_32FC1);
					hessian.at<float>(0, 0) = dxx.at<float>(j, i);
					hessian.at<float>(0, 1) = dxy.at<float>(j, i);
					hessian.at<float>(1, 0) = dxy.at<float>(j, i);
					hessian.at<float>(1, 1) = dyy.at<float>(j, i);

					Mat eValue;
					Mat eVectors;
					eigen(hessian, eValue, eVectors);

					double nx, ny;
					double fmaxD = 0;
					if (fabs(eValue.at<float>(0, 0)) >= fabs(eValue.at<float>(1, 0)))  //求特征值最大时对应的特征向量
					{
						nx = eVectors.at<float>(0, 0);
						ny = eVectors.at<float>(0, 1);
						fmaxD = eValue.at<float>(0, 0);
					}
					else
					{
						nx = eVectors.at<float>(1, 0);
						ny = eVectors.at<float>(1, 1);
						fmaxD = eValue.at<float>(1, 0);
					}

					double t = -(nx*dx.at<float>(j, i) + ny*dy.at<float>(j, i)) / (nx*nx*dxx.at<float>(j, i) + 2 * nx*ny*dxy.at<float>(j, i) + ny*ny*dyy.at<float>(j, i));

					if (fabs(t*nx) <= 0.5 && fabs(t*ny) <= 0.5)
					{
						Pt.push_back(i);
						Pt.push_back(j);
					}
				}

			}
		}
	}
	else
	{
		Min = Min < 0 ? 0 : Min;
		Max = Max > src.cols ? src.cols : Max;
		for (int i = Min; i<Max; i++)
		{
			for (int j = 0; j<src.rows; j++)
			{
				if (srcGray.at<uchar>(j, i) > gray_Thed)
				{
					Mat hessian(2, 2, CV_32FC1);
					hessian.at<float>(0, 0) = dxx.at<float>(j, i);
					hessian.at<float>(0, 1) = dxy.at<float>(j, i);
					hessian.at<float>(1, 0) = dxy.at<float>(j, i);
					hessian.at<float>(1, 1) = dyy.at<float>(j, i);

					Mat eValue;
					Mat eVectors;
					eigen(hessian, eValue, eVectors);

					double nx, ny;
					double fmaxD = 0;
					if (fabs(eValue.at<float>(0, 0)) >= fabs(eValue.at<float>(1, 0)))  //求特征值最大时对应的特征向量
					{
						nx = eVectors.at<float>(0, 0);
						ny = eVectors.at<float>(0, 1);
						fmaxD = eValue.at<float>(0, 0);
					}
					else
					{
						nx = eVectors.at<float>(1, 0);
						ny = eVectors.at<float>(1, 1);
						fmaxD = eValue.at<float>(1, 0);
					}

					double t = -(nx*dx.at<float>(j, i) + ny*dy.at<float>(j, i)) / (nx*nx*dxx.at<float>(j, i) + 2 * nx*ny*dxy.at<float>(j, i) + ny*ny*dyy.at<float>(j, i));
					if (fabs(t*nx) <= 0.5 && fabs(t*ny) <= 0.5)
					{
						Pt.push_back(i);
						Pt.push_back(j);
					}
				}
			}
		}
	}
	for (int k = 0; k<Pt.size() / 2; k++)
	{
		points_vec[k].x = Pt[2 * k + 0];
		points_vec[k].y = Pt[2 * k + 1];
	}
	return points_vec;
}

steger参考的网上算法需要调试几个参数。灰度重心法的提取图像如下图所示：

空间中两条直线可以确定一个平面，这里用了四副标板图以及上面的激光轮廓。可将其中一块标板的参考坐标系作为世界坐标系，这里将第一块标板的坐标系当做世界坐标系。另外三幅标板的作用在于将激光条纹提取的轮廓点根据相应的标板外参转到相机坐标系下，再由相机坐标和标板1的外参可将所有的轮廓点坐标转到以标板1为参考系的世界坐标。

上面这段话是理解整个标定、重构过程的精髓，理解了这段话，整个系统的理解就很简单。

 标板投射的激光图，为避免棋盘格的影响，将整个图像的亮度调低。

 提取出来的激光轮廓图，为绿颜色的线条

 光平面标定

首先加载各副标板图对应的外参，并保存下来；

读取激光条纹图，先根据相机标定的内参结果对激光轮廓图进行矫正；

矫正完后，基于灰度重心法对激光条纹轮廓进行提取，将提取的点存在vector；

将各副对应标板图的平面零点和法向量，（一个平面可由平面上的一点和法向量表示），根据其对应的标板外参转换到相机坐标系下，即转换后的标板平面为相机坐标系下的平面；

将提取的点由图像坐标系转为相机坐标系下，将该点和相机光心（相机坐标系的原点）连线，可得到一条空间直线；

求解空间直线和平面的交点即为光平面上的点。

看完理清上面这一段话，再看博文一更好理解。

线结构光三维重建（一）icon-default.png?t=M85Bhttps://blog.csdn.net/beyond951/article/details/125771158?spm=1001.2014.3001.5502

//相机标定完，保存下来各副标板图的外参
//读取外参矩阵
for (int i = 0; i < ImgSource_Vec.size(); i++)
{
	Mat rotation_matrix, translation_vectors;
	File_Help.Load_RT_Params(".\\image\\source\\" + ImgSource_Vec[i] + ".xml", rotation_matrix, translation_vectors);
	R_Vec.push_back(rotation_matrix);
	T_Vec.push_back(translation_vectors);
}
for (int i = 0; i < ImgSource_Vec.size(); i++)
{
	//先根据标定的内参矫正图像
	Mat line_src = imread(Line_path + ImgSource_Vec[i] + ".bmp");
	line_src = Api.Correct_Img(line_src, intrin_matrix, distort_coeffs);
	//灰度重心法提取激光条纹轮廓点
	vector<Point2f> Line_Points_Vec = Api.GetLinePoints_GrayWeight(line_src, 190, 1600, 2000, 1);
	//相机坐标系下标板的零点
	//相机坐标系下平面法向量
	//将世界坐标系下标板的零点和平面法向量转换到对应的相机坐标系下
	Mat Word_Zreo = (Mat_<double>(3, 1) << 0, 0, 0);
	Mat cam_Zero = R_Vec[i] * Word_Zreo + T_Vec[i];             
	Mat Plane_N = (Mat_<double>(3, 1) << 0, 0, 1);
	Mat cam_Plane_N = R_Vec[i] * Plane_N + T_Vec[i];             
	for each (Point2f L_Point in Line_Points_Vec)
	{
		//计算激光条纹点在成像面投影点
		Mat Cam_XYZ = (Mat_<double>(3, 1) << (L_Point.x - u)* 0.0024, (L_Point.y - v)*0.0024, f);
		//计算相机光心和激光条纹点在成像面投影点的连线和标板平面的交点
		Point3f point_Cam = Api.CalPlaneLineIntersectPoint(Vec3d(cam_Plane_N.at<double>(0, 0) - cam_Zero.at<double>(0, 0), cam_Plane_N.at<double>(1, 0) - cam_Zero.at<double>(1, 0), cam_Plane_N.at<double>(2, 0) - cam_Zero.at<double>(2, 0)), Point3f(cam_Zero.at<double>(0, 0), cam_Zero.at<double>(1, 0), cam_Zero.at<double>(2, 0)), Vec3f(Cam_XYZ.at<double>(0, 0), Cam_XYZ.at<double>(1, 0), Cam_XYZ.at<double>(2, 0)), Point3f(0, 0, 0));
		//将求得点进行保存
		Plane_Points_Vec.push_back(point_Cam);
	}
}
//保存点云
ofstream fout(".\\image\\word_cor_points.txt");
for each(Point3f point in Plane_Points_Vec)
{
	fout << point.x << " " << point.y << " " << point.z << endl;
}
//根据上面得到点拟合光平面
float PlaneLight[4];                            
Api.Fit_Plane(Plane_Points_Vec, PlaneLight);
//平面误差
float ems = Api.Get_Plane_Dist(Plane_Points_Vec, PlaneLight);
Mat Plane_V = (Mat_<double>(4, 1) << PlaneLight[0], PlaneLight[1], PlaneLight[2], PlaneLight[3]);

交比不变性标定

首先加载标板图对应的外参参数；

读取对应的标板图像，进行角点检测，将角点按行存储，并拟合直线（蓝线）；

读取对应的激光条纹投射的标板图，提取激光轮廓点，并进行直线拟合（黄线），求拟合直线和棋盘格行直线的交点（红点）；

求得的交点图像坐标已知，根据交比不变性，图像坐标系下的交并复比和标板坐标系下的交并复比相等，求得交点在标板上的坐标；

将求得交点在标板上的坐标根据标板对应的外参转到相机坐标系下；

将多副激光标板求得点进行平面拟合得到其在相机坐标系下的光平面。

//读取外参矩阵
	for (int i = 0; i < ImgSource_Vec.size(); i++)
	{
		Mat rotation_matrix, translation_vectors;
		File_Help.Load_RT_Params(".\\image\\source\\" + ImgSource_Vec[i] + ".xml", rotation_matrix, translation_vectors);
		R_Vec.push_back(rotation_matrix);
		T_Vec.push_back(translation_vectors);
	}

	for (int i = 0; i < ImgSource_Vec.size(); i++)
	{
		//读取标板图像
		Mat src = imread(Chess_path + ImgSource_Vec[i] + ".bmp");
		//根据标定的相机内参先对图像进行校正
		Mat Correct = Api.Correct_Img(src, intrin_matrix, distort_coeffs);
		//提取标板图像上面棋盘格的角点
		vector<Point2f> corners = Api.Get_Conners(Correct, Conner_Size, ".\\image\\line_Image\\" + ImgSource_Vec[i], 0);
		//标板角点按行进行直线拟合
		vector<vector<Point2f>> Lines_Points;
		Mat LineImg = src.clone();
		vector<Vec4f> Chess_Lines; 
		//按行存储
		for (int j = 0; j < Conner_Size.width; j++)
		{
			vector<Point2f> line_points;
			for (int k = 0; k < Conner_Size.height; k++)
			{
				line_points.push_back(corners[j + k*Conner_Size.width]);
				circle(LineImg, corners[j + k*Conner_Size.width], 2, Scalar(0, 0, 255), 2, 8, 0);
			}
			Lines_Points.push_back(line_points);
		}
		//直线拟合	
		for each (vector<Point2f> points in Lines_Points)
		{
			Vec4f corner_line_fit_temp;
			fitLine(points, corner_line_fit_temp, CV_DIST_L2, 0, 0.01, 0.01);
			//直线拟合
			Chess_Lines.push_back(corner_line_fit_temp);
			Mat Temp;
			Api.CVT_Gray2RGB(src, Temp);
			//图片转换
			CvPoint2D32f startpt;
			CvPoint2D32f endpt;
			//直线起点&终点
			Api.getFitLineStartEndPt(Temp, corner_line_fit_temp, startpt, endpt);     
			line(LineImg, startpt, endpt, Scalar(0, 255, 0), 1);
		}
		//首先灰度重心法对激光条纹进行轮廓点进行提取
		//根据提取到的轮廓点进行直线拟合
		Vec4f lightline_fitline;
		//读取标板图对应的激光标板图
		Mat line_src = imread(Line_path + ImgSource_Vec[i] + ".bmp");
		//校正图像
		line_src = Api.Correct_Img(line_src, intrin_matrix, distort_coeffs);
		//灰度重心法提取激光轮廓中心点
		vector<Point2f> Line_Points_Vec = Api.GetLinePoints_GrayWeight(line_src, 254, 1700, 2300, 1);
		//直线拟合
		fitLine(Line_Points_Vec, lightline_fitline, CV_DIST_L12, 0, 0.01, 0.01);        
		Mat Temp;
		//图片转换
		Api.CVT_Gray2RGB(line_src, Temp);                                             
		CvPoint2D32f startpt;
		CvPoint2D32f endpt;
		//直线起点&终点
		Api.getFitLineStartEndPt(Temp, lightline_fitline, startpt, endpt);     
		line(line_src, startpt, endpt, Scalar(0, 255, 0), 1);
		//保存灰度重心法提取光条直线的图片
		imwrite(Line_path + ImgSource_Vec[i] + "_FitLine.bmp", line_src); 
		//棋盘格角点每一行拟合的直线和激光条纹拟合直线的交点
		vector<Point2f> cross_vec;        
		for each (Vec4f line in Chess_Lines)
		{
			/*求交点并画点保存，result.jpg存储在工程目录下*/
			Point2f crossPoint;
			crossPoint = Api.getCrossPoint(line, lightline_fitline);
			cross_vec.push_back(crossPoint);
			circle(LineImg, crossPoint, 3, Scalar(255, 0, 0), 2, 8, 0);
		}
		line(LineImg, startpt, endpt, Scalar(0, 255, 0), 1);
		imwrite(".\\image\\line_Image\\" + ImgSource_Vec[i] + "_Final.bmp", LineImg);
		//激光线标板坐标系坐标提取（交比不变性）
		//根据标板坐标系和图像坐标系的交并复比不变性
		//求取交点在靶标坐标系上的点坐标
		vector<Point3f> Cor_Points;   //标板坐标系激光点
		vector<Point3f> Cam_Points;   //相机坐标系激光点
		for (int m = 0; m < Lines_Points.size(); m++)
		{
			vector<Point2f> Chess_points = Lines_Points[m];   //图像坐标系：标板直线角点
			//图像坐标系的交并复比
			double AC = Api.Point2Point_Dist(Chess_points[10], Chess_points[5]);
			double AD = Api.Point2Point_Dist(Chess_points[10], Chess_points[0]);
			double BC = Api.Point2Point_Dist(cross_vec[m], Chess_points[5]);
			double BD = Api.Point2Point_Dist(cross_vec[m], Chess_points[0]);
			double SR = (AC / BC) / (AD / BD);
			//标板坐标系的交并复比
			//棋盘格一格距离代表2mm
			double ac = (10 - 5) * 2;
			double ad = (10 - 0) * 2;
			double X1 = (ad*SR * 2 * 5 - ac * 2 * 0) / (ad*SR - ac);
			AC = Api.Point2Point_Dist(Chess_points[10], Chess_points[5]);
			AD = Api.Point2Point_Dist(Chess_points[10], Chess_points[4]);
			BC = Api.Point2Point_Dist(cross_vec[m], Chess_points[5]);
			BD = Api.Point2Point_Dist(cross_vec[m], Chess_points[4]);
			SR = (AC / BC) / (AD / BD);
			ac = (10 - 5) * 2;
			ad = (10 - 4) * 2;
			double X2 = (ad*SR * 2 * 5 - ac * 2 * 4) / (ad*SR - ac);
			float x = (X1 + X2) / 2.0f;
			Point3f Point = Point3f(x, m * 2, 0);
			Cor_Points.push_back(Point);
			//将标板上的交点坐标根据标板对应的外参转到相机坐标系
			Mat cam_Point = (Mat_<double>(3, 1) << x, m * 2, 0);
			Mat Trans_Mat = (Mat_<double>(3, 1) << 0, 0, 0);
			Trans_Mat = R_Vec[i] * cam_Point + T_Vec[i];
			Point3f Trans_Point = Point3f(Trans_Mat.at<double>(0, 0), Trans_Mat.at<double>(1, 0), Trans_Mat.at<double>(2, 0));
			Plane_Points_Vec.push_back(Trans_Point);
		}
	}
	//根据点进行平面拟合
	float PlaneLight[4];                             
	Api.Fit_Plane(Plane_Points_Vec, PlaneLight);
	//平面拟合的误差
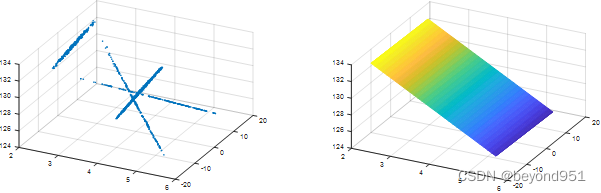
	float ems = Api.Get_Plane_Dist(Plane_Points_Vec, PlaneLight);

最后得到的光平面如下

Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

“源”聚天大，码动未来|开放原子校源行（天津大学站）即将启幕！

11月22日，开放原子校源行（天津大学站）将在天津大学北洋园校区隆重举办。

avatar 开放原子开发者工作坊

openEuler系累计装机量突破1000万，树立操作系统产业新里程碑

11月15日，以“以智能，致世界”为主题的操作系统大会2024在北京中关村国际创新中心召开。

avatar 开放原子开发者工作坊

多模态大模型&科学计算双管齐下，百度飞桨两大赛项报名倒计时！

第二届开放原子大赛是由开放原子开源基金会组织举办的开源技术领域专业赛事，聚焦解决真问题，重点覆盖基础软件、工业软件、人工智能大模型等领域

avatar 开放原子开发者工作坊