Spring-_-Bear 的 CSDN 博客导航

文章目录

一、实验目标

  1. 掌握图的定义和图的存储结构。
  2. 掌握图的创建方法和图的应用。
  3. 使用 C++ 语言，定义图的数据结构，结合迭代开发思路实现 “景区信息管理系统”。

二、实验任务

2.1 任务背景

现有一个景区，景区里面有若干个景点，景点之间满足以下条件：

  1. 某些景点之间铺设了道路（相邻）。
  2. 这些道路都是可以双向行驶的（无向图）。
  3. 从任意一个景点出发都可以游览整个景区（连通图）。

开发景区信息管理系统，对景区的信息进行管理。使用图的数据结构来保存景区景点信息，为用户提供创建图、查询景点信息、旅游景点导航、搜索最短路径、铺设电路规划等功能。

在这里插入图片描述

2.2 景点数据

景区的数据包含景点信息和景点之间的道路信息。分别由两个文本文件 Vex.txt 和 Edge.txt 存储。

2.2.1 Vex.txt

Vex.txt：存储景点信息，文件第 1 行记录景区的景点总个数。从第 2 行开始，每 3 行记录一个景点信息。 每个景点信息的记录格式为：

  1. 景点编号（编号从 0 开始，逐个加 1）
  2. 景点名字
  3. 景点介绍
7
0
A区
风景优美，气候宜人。门票10元。
1
B区
风景优美，气候宜人。门票20元。
2
C区
风景优美，气候宜人。门票30元。
3
D区
风景优美，气候宜人。门票40元。
4
E区
风景优美，气候宜人。门票50元。
5
F区
风景优美，气候宜人。门票60元。
6
G区
风景优美，气候宜人。门票70元。

2.2.2 Edge.txt

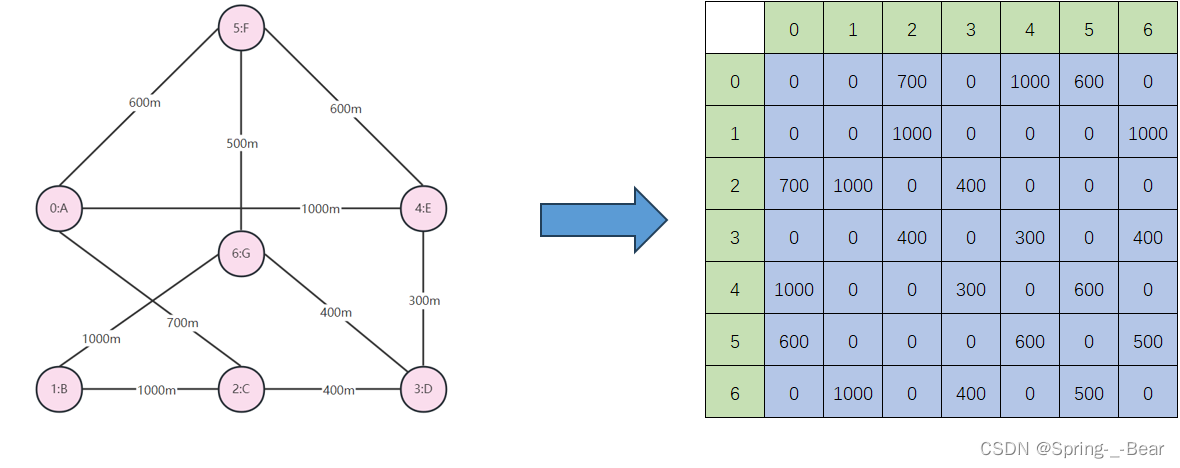
Edge.txt：存储道路信息，文件中每 1 行记录 1 条道路信息。格式为 “景点1的编号 景点2的编号 道路的长度”，每条记录使用空格符进行分割。 若文件中没有某两个景点的信息，就表示这两个景点之间没有直接的路径。

0	2	700
0	4	1000
0	5	600
1	2	1000
1	6	1000
2	3	400
3	4	300
3	6	400
4	5	600
5	6	500

2.3 任务要求

在这里插入图片描述

三、分析和设计

程序输入的数据，可从文件中直接读取，也可以从界面中输入。本程序将直接从 Vex.txt 和 Edge.txt 这两个文件中读取数据，采用图的存储结构，应用深度优先搜索算法 (DFS)、迪杰斯特拉 (Dijkstra) 算法、普里姆 (Prim) 算法等，开发景区信息管理系统。

3.1 程序设计

使用 Mircosoft Visual Studio 2019 开发工具，创建一个空的控制台工程 (Win32 Console Application)。利用图的存储结构来保存景区景点图，使用 C++ 语言开发景区信息管理系统，工程名为 GraphCPro。

  1. 添加 Graph.h 和 Graph.cpp 文件，用来定义图的数据结构，实现图的相关操作。
  2. 添加 Tourism.h 和 Tourism.cpp 文件，用来实现景区信息管理系统的相关功能。
  3. 添加 Main.cpp 文件，在文件中创建程序入口函数 int main(void)。

3.2 界面设计

在 int main(void) 函数中输出菜单，将系统功能列出来，供用户选择。使用 while 循环输出主菜单。使用 cin 获得用户的输入，使用 switch-case 语句判断具体是哪个功能。

选择功能
1创建景区景点图
2查询景点信息
3旅游景点导航
4搜索最短路径
5铺设电路规划
0退出

3.3 数据结构设计

3.3.1 图的存储

当保存图结构时，即要保存顶点信息，也要保存边。图可用数组或链表来存储。

  1. 数组表示，常用一维数组来保存顶点的集合，使用二维数组来保存边的集合；
  2. 链表表示，常用邻接表、十字链表等方式存储图的顶点和边的信息。

本程序中使用数组表示法存储图：

  • 定义一维数组 Vex m_aVexs[20] 保存顶点信息，最多允许有 20 个顶点。
  • 定义二维数组 (邻接矩阵) int m_AdjMatrix[20][20] 保存边的集合，数组中每个元素的值即为边的权值。

3.3.2 景区景点图

景区的地图可以看做是一个带权无向图，使用邻接矩阵来保存。

  1. 景区中的所有景点即为图的顶点。
  2. 当两个景点之间铺设的有道路时，表示两个顶点相连，为一条边。
  3. 两个景点之间的距离，即为边的权值。权值为 0 表示两个顶点不相连。

在这里插入图片描述

3.3.3 顶点和边的信息

定义 Vex 结构体，存储图的顶点信息。

struct Vex
{
    int num;         // 景点编号
    char name[20];   // 景点名字
    char desc[1024]; // 景点介绍
};

定义 Edge 结构体，存储图的边的信息。

struct Edge
{
    int vex1;   // 边的第一个顶点
    int vex2;   // 边的第二个顶点
    int weight; // 权值
};

四、运行示例

4.1 系统欢迎界面

在这里插入图片描述

4.2 系统菜单选择

在这里插入图片描述

4.3 创建景区景点图

在这里插入图片描述

4.4 查询景点信息

在这里插入图片描述

4.5 旅游景点导航

在这里插入图片描述

4.6 搜索最短路径

在这里插入图片描述

4.7 铺设电路规划

在这里插入图片描述

4.8 退出系统

在这里插入图片描述

五、程序源码

注：需将 Vex.txt 和 Edge.txt 文件拷贝到源码目录下。

5.1 main.cpp

#define _CRT_SECURE_NO_WARNINGS

#include <iostream>

#include "Tourism.h"
#include "Graph.h"

using namespace std;

Graph m_Graph;

int main(void)
{
	int choice;

	// 系统界面
	printf("\n\n\n\n\n\n\n\n\n\n\n\n\n\n\t\t\t\t\t\t");
	printf("*欢迎进入景区管理系统*");
	printf("\n\n\n\n\n\n\n\n\n\n\n\n\n\t\t\t\t\t\t");
	system("pause");
	system("cls");

	do
	{
		// 输出系统菜单
		cout << "=====景区信息管理系统=====" << endl;
		cout << "*    1.创建景区景点图    *" << endl;
		cout << "*    2.查询景点信息      *" << endl;
		cout << "*    3.旅游景点导航      *" << endl;
		cout << "*    4.搜索最短路径      *" << endl;
		cout << "*    5.铺设电路规划      *" << endl;
		cout << "*    0.退出              *" << endl;
		cout << "==========================" << endl;

		// 用户选择功能
		cout << "请输入菜单项编号(0-5):";
		cin >> choice;
		cout << endl;

		switch (choice)
		{
		case 1:
			CreateGraph();
			break;
		case 2:
			GetSpotInfo();
			break;
		case 3:
			TravelPath();
			break;
		case 4:
			FindShortPath();
			break;
		case 5:
			DesignPath();
			break;
		case 0:
			cout << "谢谢您使用本系统！" << endl;
			break;
		default:
			cout << "您的输入有误！请重新输入！" << endl
				 << endl;
		}

	} while (choice != 0);

	return 0;
}

5.2 Graph.h

#pragma once

// 存储图的顶点信息
struct Vex
{
	int num;		 // 景点编号
	char name[20];	 // 景点名字
	char desc[1024]; // 景点介绍
};

// 存储边的信息
struct Edge
{
	int vex1;	// 边的第一个顶点
	int vex2;	// 边的第二个顶点
	int weight; // 权值
};

// 顶点数组和邻接矩阵，用来保存图的信息
struct Graph
{
	int m_aAdjMatrix[20][20]; // 邻接矩阵
	Vex m_aVexs[20];		  // 顶点信息数组
	int m_nVexNum;			  // 当前图的顶点个数
};

// 定义链表 PathList 来保存所有路径
typedef struct Path
{
	int vexs[20]; // 保存一条路径
	Path *next;	  // 下一条路径
} *PathList;

// 初始化图
void Init(void);
// 插入顶点信息
bool InsertVex(Vex sVex);
// 插入边的信息
bool InsertEdge(Edge sEdge);
// 通过传入的顶点编号，返回对应顶点信息结构体
Vex GetVex(int v);
// 查询所有与指定顶点相连的边
int FindEdge(int v, Edge aEdge[]);
// 使用深度优先搜索算法遍历图
void DFS(int nVex, bool isVisited[], int &nIndex, PathList &pList);
// 通过调用 DFS 函数，得到深度有限搜索遍历的结果
void DFSTraverse(int nVex, PathList &pList);
// 寻找最短路径
int FindShortPath(int nVexStart, int nVexEnd, Edge aPath[]);
// 通过 Prim 算法构建最小生成树
void FindMinTree(Edge aPath[]);

5.3 Graph.cpp

#define _CRT_SECURE_NO_WARNINGS

#include <iostream>

#include "Graph.h"

extern Graph m_Graph;

// 函数名：Init
// 参数：void
// 返回值：void
// 功能：实现图的初始化，权值信息都初始化为0
void Init(void)
{
	for (int i = 0; i < 20; i++)
	{
		for (int j = 0; j < 20; j++)
		{
			m_Graph.m_aAdjMatrix[i][j] = 0; // 权值信息初始化为0
		}
		m_Graph.m_nVexNum = 0; // 景点数目初始化为0
	}
}

// 函数名：InsertVex
// 参数：结构体vex
// 返回值：true：顶点未满   false：顶点已满
// 功能：通过传入结构体，将顶点的相关信息插入到顶点信息数组中
bool InsertVex(Vex sVex)
{
	if (m_Graph.m_nVexNum == 20)
	{
		// 顶点已满
		return false;
	}
	m_Graph.m_aVexs[m_Graph.m_nVexNum++] = sVex; // 插入顶点信息
	return true;
}

// 函数名：InsertEdge
// 参数：Edge结构体
// 返回值：true:插入成功   false：下表越界
// 功能：通过传入Edge结构体，将边的相关信息插入到权值矩阵中
bool InsertEdge(Edge sEdge)
{
	if (sEdge.vex1 < 0 || sEdge.vex1 >= m_Graph.m_nVexNum || sEdge.vex2 < 0 || sEdge.vex2 >= m_Graph.m_nVexNum)
	{
		// 下标越界
		return false;
	}
	// 插入边的信息
	m_Graph.m_aAdjMatrix[sEdge.vex1][sEdge.vex2] = sEdge.weight;
	m_Graph.m_aAdjMatrix[sEdge.vex2][sEdge.vex1] = sEdge.weight;
	return true;
}

// 函数名：GetVex
// 参数：输入的编号
// 返回值：对应编号的顶点信息结构体
// 功能：通过传入的顶点编号，返回对应顶点信息结构体
Vex GetVex(int v)
{
	return m_Graph.m_aVexs[v];
}

// 函数名：FindEdge
// 参数：nVex:想要查询的顶点   aEdge[]:
// 返回值：边的条数
// 功能：查询与指定顶点相连的边
int FindEdge(int nVex, Edge aEdge[])
{
	int k = 0;

	// 遍历整个图的邻接矩阵
	for (int i = 0; i < 20; i++)
	{
		if (m_Graph.m_aAdjMatrix[nVex][i] != 0 && nVex != i)
		{
			// 得到边的信息
			aEdge[k].vex1 = nVex;
			aEdge[k].vex2 = i;
			aEdge[k].weight = m_Graph.m_aAdjMatrix[nVex][i];
			k++;
		}
	}
	return k;
}

// 函数名：DFS
// 参数：int nVex:顶点编号  bVisted[]:bool类型的数组，用来记录某个顶点是否被遍历过   int &nIndex:记录遍历深度   PathList &pList:遍历得到的结果
// 返回值：void
// 功能：使用深度优先搜索算法遍历图
void DFS(int nVex, bool isVisited[], int &nIndex, PathList &pList)
{
	isVisited[nVex] = true;		  // 修改为已访问
	pList->vexs[nIndex++] = nVex; // 访问顶点nVex

	int num = 0; // 被访问过的节点数
	for (int i = 0; i < m_Graph.m_nVexNum; i++)
	{
		if (isVisited[i])
		{ // 如果当前i节点被访问过，则num++
			num++;
		}
	}

	if (num == m_Graph.m_nVexNum)
	{ // 如果所有节点都被访问过
		// 保存一条路径
		pList->next = new Path;
		for (int i = 0; i < m_Graph.m_nVexNum; i++)
		{
			pList->next->vexs[i] = pList->vexs[i];
		}
		pList = pList->next;
		pList->next = NULL;
	}
	else
	{
		for (int w = 0; w < m_Graph.m_nVexNum; w++)
		{ // 搜索v的所有邻接点
			if (m_Graph.m_aAdjMatrix[nVex][w] > 0 && !isVisited[w])
			{									  // 如果w是nVex的邻接点并未被访问
				DFS(w, isVisited, nIndex, pList); // 递归调用DFS
				isVisited[w] = false;			  // 改为未访问
				nIndex--;						  // 索引值减1
			}
		}
	}
}

// 函数名：DFSTraverse
// 参数：int nVex：顶点编号   PathList &pList：遍历得到的结果
// 返回值：void
// 功能：通过调用DFS（）函数，得到深度有限搜索遍历的结果
void DFSTraverse(int nVex, PathList &pList)
{
	int nIndex = 0;
	bool bVisited[20] = {false};
	DFS(nVex, bVisited, nIndex, pList);
}

// 函数名：FindShortPath
// 功能：寻找最短路径
// 参数：景点的起始跟目的编号；边的路径结构数组
// 返回值：nIndex
int FindShortPath(int nVexStart, int nVexEnd, Edge aPath[])
{
	int nShortPath[20][20]; // 最短路径，行表示终点，列表示从起点到终点的最短路径的每一步
	int nShortDistance[20]; // 保存从起点到任一顶点的最短距离
	bool aVisited[20];		// 判断某点是否已在最短路径中
	int v;					// 每一次找到的可以加入集合的顶点

	// 初始化
	for (v = 0; v < m_Graph.m_nVexNum; v++)
	{
		aVisited[v] = false;

		if (m_Graph.m_aAdjMatrix[nVexStart][v] != 0)
		{
			// 如果顶点v和nVexStart相连，则最短距离设置为两顶点间的距离
			nShortDistance[v] = m_Graph.m_aAdjMatrix[nVexStart][v];
		}
		else
		{
			// 如果不相连，则最短距离设置为最大值
			nShortDistance[v] = 0x7FFFFFFF;
		}

		nShortPath[v][0] = nVexStart; // 起始点为nVexStart
		// 初始化最短路径
		for (int w = 1; w < m_Graph.m_nVexNum; w++)
		{
			nShortPath[v][w] = -1;
		}
	}
	// 初始化，将nVexStart顶点加入到集合中
	aVisited[nVexStart] = true;

	int min; // 暂存路径的最小值
	for (int i = 1; i < m_Graph.m_nVexNum; i++)
	{
		min = 0x7FFFFFFF;
		bool bAdd = false; // 判断是否还有顶点可以加入集合

		for (int w = 0; w < m_Graph.m_nVexNum; w++)
		{
			if (!aVisited[w] && nShortDistance[w] < min)
			{
				v = w;					 // w顶点距离nVexStart顶点最近
				min = nShortDistance[w]; // w到nVexStart的最短距离为min
				bAdd = true;
			}
		}
		// 如果没有顶点可以加入到集合，则跳出循环
		if (!bAdd)
		{
			break;
		}

		aVisited[v] = true;	  // 将w顶点加入到集合
		nShortPath[v][i] = v; // 每次找到最短路径后，就相当于从源点出发到了终点，所以nShortPath[v][i]=v

		for (int w = 0; w < m_Graph.m_nVexNum; w++)
		{
			// 将w作为中间点计算nVexStart到所有顶点的最短距离
			if (!aVisited[w] && (min + m_Graph.m_aAdjMatrix[v][w] < nShortDistance[w]) && (m_Graph.m_aAdjMatrix[v][w] > 0))
			{
				// 如果有新的最短距离,则更新最短路径及距离
				nShortDistance[w] = min + m_Graph.m_aAdjMatrix[v][w];
				for (int i = 0; i < m_Graph.m_nVexNum; i++)
				{
					// 如果通过w到达顶点i的距离比较短，则将w的最短路径赋值给i
					nShortPath[w][i] = nShortPath[v][i];
				}
			}
		}
	}

	int nIndex = 0;
	int nVex1 = nVexStart;

	// 将最短路径保存到边的结构体数组中
	for (int i = 1; i < m_Graph.m_nVexNum; i++)
	{
		if (nShortPath[nVexEnd][i] != -1)
		{
			aPath[nIndex].vex1 = nVex1;
			aPath[nIndex].vex2 = nShortPath[nVexEnd][i];
			aPath[nIndex].weight = m_Graph.m_aAdjMatrix[nVex1][aPath[nIndex].vex2];
			nVex1 = nShortPath[nVexEnd][i];
			nIndex++;
		}
	}
	return nIndex;
}

// 函数名：FindMinTree
// 功能：通过Prim算法构建最小生成树
// 参数：Edge aPath[]
// 返回值：void
void FindMinTree(Edge aPath[])
{
	bool aVisited[20] = {false}; // 判断某顶点是否在最小生成树中
	aVisited[0] = true;			 // 从0号顶点开始，加入到集合中
	int min;
	int nVex1, nVex2;

	for (int k = 0; k < m_Graph.m_nVexNum - 1; k++)
	{
		min = 0X7FFFFFFF;

		for (int i = 0; i < m_Graph.m_nVexNum; i++)
		{
			// 从集合中取一个顶点
			if (aVisited[i])
			{
				for (int j = 0; j < m_Graph.m_nVexNum; j++)
				{
					// 从不在集合的顶点中取出一个顶点
					if (!aVisited[j])
					{
						if ((m_Graph.m_aAdjMatrix[i][j] < min) && (m_Graph.m_aAdjMatrix[i][j] != 0))
						{
							nVex1 = i;
							nVex2 = j;
							// 找出最短边
							min = m_Graph.m_aAdjMatrix[i][j];
						}
					}
				}
			}
		}

		// 保存最短边的两个顶点
		aPath[k].vex1 = nVex1;
		aPath[k].vex2 = nVex2;
		aPath[k].weight = m_Graph.m_aAdjMatrix[nVex1][nVex2];

		// 将两个顶点加入集合
		aVisited[nVex1] = true;
		aVisited[nVex2] = true;
	}
}

5.4 Tourism.h

#pragma once

// 读取文件，创建景区景点图
void CreateGraph(void);
// 调用 GetVex() 函数，得到所有顶点信息并输出
void GetSpotInfo(void);
// 通过调用 DFSTraverse() 函数，实现旅游景点导航功能，将查询到的景点导航路线显示在界面上
void TravelPath();
// 调用 Graph.cpp 文件中的 FindShortPath() 函数查询两个景点间的最短路径和距离
void FindShortPath(void);
// 查询铺设电路规划图
void DesignPath();

5.5 Tourism.cpp

#define _CRT_SECURE_NO_WARNINGS

#include <iostream>
#include <fstream>
#include <string.h>
#include <stdlib.h>

#include "Graph.h"

using namespace std;

extern Graph m_Graph;

// 函数名：LoadVex
// 参数：void
// 返回值：void
// 功能：实现从Vex.txt文件中读取景点信息并输出
void LoadVex(void)
{
	ifstream VexFile("Vex.txt");
	if (!VexFile)
	{
		cout << "Vex.txt文件打开失败，请检查！" << endl;
		return;
	}

	// 暂存从Vex.txt读取到的一行数据
	char num[2];
	char name[20];
	char desc[1024];
	Vex sVex;

	// 逐行读取Vex.txt中的数据
	VexFile.getline(num, 2); // 将第一行的数据读出丢掉

	cout << "景区数目：" << atoi(num) << endl;
	cout << "-----顶点-----" << endl;
	// 将顶点信息保存到顶点数组中
	while (VexFile.getline(num, 2))
	{
		sVex.num = atoi(num);
		VexFile.getline(name, 20);
		strcpy(sVex.name, name);
		VexFile.getline(desc, 1024);
		strcpy(sVex.desc, desc);

		// 将顶点信息输出
		cout << sVex.num << "-" << sVex.name << endl;

		// 设置图的顶点
		if (!InsertVex(sVex))
		{
			cout << "新增景点失败！" << endl;
			continue;
		}
	}
	cout << "------------" << endl;
	VexFile.close();
}

// 函数名：LoadPath
// 参数：void
// 返回值：void
// 功能：实现从Edge.txt文件中读取路径信息并输出
void LoadPath()
{
	ifstream EdgeFile("Edge.txt");
	if (!EdgeFile)
	{
		cout << "Edge.txt文件打开失败，请检查！" << endl;
		return;
	}

	Edge edge;
	cout << "------边------" << endl;
	while (EdgeFile)
	{
		EdgeFile >> edge.vex1 >> edge.vex2 >> edge.weight;
		cout << "<" << edge.vex1 << "," << edge.vex2 << ">   " << edge.weight << endl;

		// 设置图的边
		if (!InsertEdge(edge))
		{
			cout << "新增路径信息失败！" << endl;
			continue;
		}
	}
	cout << "-------------" << endl;
	EdgeFile.close();
	cout << "======================" << endl;
}

// 函数名:CreateGraph
// 参数：void
// 返回值：void
// 功能：读取文件，获取景点信息和道路信息
void CreateGraph(void)
{
	cout << "\n=====创建景点景区图=====" << endl;

	Init();		// 初始化图
	LoadVex();	// 从Vex.txt文件中读取景点信息并输出
	LoadPath(); // 从Edge.txt文件中读取路径信息并输出
	cout << endl;
}

// 函数名：GetSpotInfo
// 参数：void
// 返回值：void
// 功能：调用GetVex（）函数，得到所有顶点信息并输出
void GetSpotInfo(void)
{
	cout << "\n=====查询景点信息=====" << endl;
	int nVexNum = m_Graph.m_nVexNum;
	if (nVexNum == 0)
	{
		cout << "请先创建图！" << endl;
		return;
	}

	// 将景点信息罗列出来，供用户查询选择
	for (int i = 0; i < m_Graph.m_nVexNum; i++)
	{
		Vex sVex = GetVex(i);
		cout << i << "-" << sVex.name << endl;
	}

	cout << "====================" << endl;

	// 提示用户根据编号进行查询
	cout << "\n请输入想要查询的景点编号：";
	int num;
	cin >> num;

	if (num < 0 || num >= m_Graph.m_nVexNum)
	{
		cout << "您的输入有误！请重新输入！" << endl;
		cout << "\n请输入想要查询的景点编号：";
		cin >> num;
	}
	else
	{
		Vex sVex = GetVex(num);
		cout << "----------------------------" << endl;
		cout << sVex.name << ":" << sVex.desc << endl;
		cout << "----------------------------" << endl;
		cout << "-----周边景区-----" << endl;
		Edge aEdge[20];
		int EdgeNum = FindEdge(num, aEdge);
		for (int i = 0; i < EdgeNum; i++)
		{
			Vex v1 = GetVex(aEdge[i].vex1);
			Vex v2 = GetVex(aEdge[i].vex2);
			cout << v1.name << "->" << v2.name << "   " << aEdge[i].weight << "m" << endl;
		}
		cout << "------------------" << endl;
	}
	cout << endl;
}

// 函数名：TravelPath
// 参数：void
// 返回值：void
// 功能：通过调用DFSTraverse（）函数，实现旅游景点导航功能，将查询到的景点导航路线显示在界面上
void TravelPath()
{
	cout << "\n=======旅游景点导航======" << endl;

	int nVexNum = m_Graph.m_nVexNum;
	if (nVexNum == 0)
	{
		cout << "请先创建图！" << endl;
		return;
	}

	for (int i = 0; i < m_Graph.m_nVexNum; i++)
	{
		Vex sVex = GetVex(i);
		cout << "*\t" << i << "-" << sVex.name << "\t\t*" << endl;
	}
	cout << "=========================" << endl;

	// 输入景点编号
	cout << "请输入想要导航的起始点编号：";
	int startNum;
	cin >> startNum;
	if (startNum < 0 || startNum >= m_Graph.m_nVexNum)
	{
		cout << "您输入的编号有误！" << endl;
		return;
	}

	// 遍历景区景点图
	PathList pList = new Path;
	PathList pHead = pList;
	DFSTraverse(startNum, pList);

	cout << endl;

	// 输出遍历结果
	cout << "导航路线为：" << endl;
	int i = 1;
	pList = pHead;
	while (pList->next != NULL)
	{
		Vex vex = GetVex(pList->vexs[0]);
		cout << "路线" << i++ << ":" << vex.name;
		for (int j = 1; j < m_Graph.m_nVexNum; j++)
		{
			vex = GetVex(pList->vexs[j]);
			cout << "->" << vex.name;
		}
		cout << endl;
		pList = pList->next;
	}
	cout << endl;

	delete pList;
	pList = NULL;
	pHead = NULL;
}

// 函数名：FindShortPath
// 功能：调用Graph.cpp文件中的FindShortPath函数查询两个景点间的最短路径和距离
// 参数：void
// 返回值：void
void FindShortPath(void)
{
	cout << "\n======搜索最短路径======\n";

	int nVexNum = m_Graph.m_nVexNum;

	if (nVexNum == 0)
	{
		cout << "请先创建图！" << endl;
		return;
	}

	for (int i = 0; i < m_Graph.m_nVexNum; i++)
	{
		Vex sVex = GetVex(i);
		cout << "*\t" << i << "-" << sVex.name << "\t\t*" << endl;
	}
	cout << "========================\n";

	// 输入两个景点的编号
	int start_place, end_place;
	cout << "请输入起点的编号：";
	cin >> start_place;
	cout << "请输入终点的编号：";
	cin >> end_place;

	if (start_place < 0 || start_place >= m_Graph.m_nVexNum || end_place < 0 || end_place >= m_Graph.m_nVexNum)
	{
		cout << "输入错误！请重新输入！！！" << endl;
		return;
	}

	Edge aPath[20]; // 边信息数组，依次保存最短的路径

	for (int i = 0; i < 20; i++)
	{
		// 初始化边信息数组
		aPath->vex1 = -1;
		aPath->vex2 = -1;
		aPath->weight = -1;
	}

	// 搜索最短路径
	int index = FindShortPath(start_place, end_place, aPath);
	int length = 0; // 最短路径总长度
	Vex sVex = GetVex(aPath[0].vex1);

	// 得到最短路径和最短距离
	cout << "\n最短路径为：" << sVex.name;

	for (int i = 0; i < index; i++)
	{
		sVex = GetVex(aPath[i].vex2);
		cout << "->" << sVex.name;
		length += aPath[i].weight;
	}

	cout << endl;
	cout << "最短距离为:" << length << "米" << endl
		 << endl;
}

// 函数名：DesignPath
// 功能：查询电路铺设规划图
// 参数：void
// 返回值：void
void DesignPath()
{
	cout << "在以下两个景点之间铺设电路";
	cout << "\n=======铺设电路规划=======" << endl;

	Edge aPath[20];

	FindMinTree(aPath); // 构建最小树

	int nVexNum = m_Graph.m_nVexNum;

	if (nVexNum == 0)
	{
		cout << "请先创建图！" << endl;
		return;
	}

	// 输出铺设线路图
	int nAllLength = 0;

	for (int i = 0; i < m_Graph.m_nVexNum - 1; i++)
	{
		Vex nVex1 = GetVex(aPath[i].vex1);
		Vex nVex2 = GetVex(aPath[i].vex2);

		cout << "\t" << nVex1.name << "-" << nVex2.name << ":" << aPath[i].weight << "m" << endl;
		nAllLength += aPath[i].weight;
	}
	cout << "==========================\n";
	cout << "铺设电路的总长度是：" << nAllLength << "m" << endl
		 << endl;
}
# c++
Logo
开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

cover

一文解决Cellphonedb单细胞互作分析及可视化作图（2）

avatar 开放原子开发者工作坊
cover

[工具使用]——时序图与UML类图

avatar 开放原子开发者工作坊

CTFHub技能树 Web-SQL注入 详解

整数型注入我们输入 1不断尝试发现闭合方式就是 1 ，整数型存在两列order by 2存在两个注入点/?id=-1 union select 8,9爆库，当前数据库为sqli/?id=-1 union select 8,database()爆出所有表名,这里我们需要吧sqli转换为16进制/?id=-1 union select 8,group_concat(table_name) from i

avatar 开放原子开发者工作坊