符号说明

模型建立

根据上述变量定义，建立含安全约束的机组最优组合（SCUC）模型如下：

目标函数

目标函数即为最小化成本，包括发电带来的煤耗成本和机组启停产生的开停机成本                         

其中，机组的煤耗函数可用出力的二次函数表述：

等式约束条件

此即为系统的功率平衡约束。

不等式约束条件

(1)热备用                       

(2)机组出力约束

(3)机组爬坡约束    

(4)机组起停时间约束                                                                

(5)起停费用约束

(6) 潮流安全约束

当机组启动最小出力大于爬坡速率，机组爬坡约束将使得所有关停的机组都无法启动，因此改写为

其中，为了简化，可以将启动最大升速率和停机最大降速率都取为

 计算潮流的转移分布因子矩阵，将潮流安全约束改写为

其中描述节点ii的注入功率对于线路l产生的影响。则简化模型的变量为和，在满足约束下，最小化目标函数。

模型简化

由上小节构建的机组组合优化模型，煤耗成本采用二次函数，当系统规模较大时（如节点数超过1000），求解起来将消耗大量时间。因此我们可以对原模型进行线性化处理。

将煤耗函数分段线性化，分为m段，将原模型煤耗函数的替换为

其中，  \[{{K}_{i,s}}\]代表分段线性化后煤耗函数各段斜率，\[{{C}_{0,i}}\]表示机组开机并以最小出力${{P}_{i,\min }}$运行产生的煤耗，${{p}_{i,t,s}}$为机组分段的出力，满足下式：

 算例 ​​​​​​

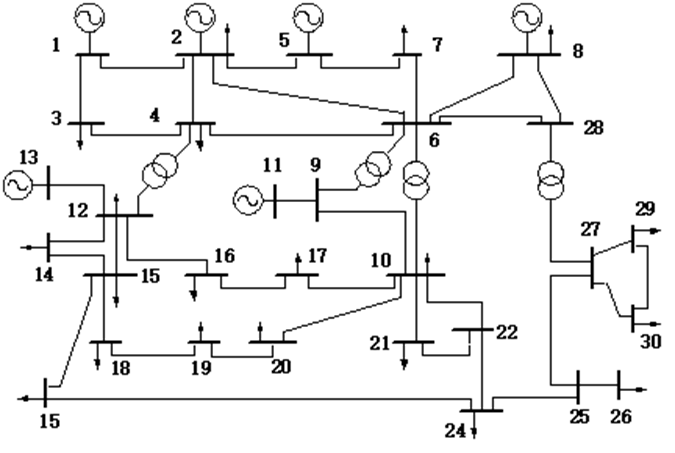
校验程序的算例基于IEEE-30节点标准测试系统，系统接线图如图1。系统包含30个节点，6台发电机组。要求确定系统最优机组组合，使得系统各机组总运行成本（煤耗成本+启停成本）最小化。

 图1. IEEE-30节点测试系统接线

已知：给定系统数据包括如下：

线路网络参数：

编号	首端节点	末端节点	支路电抗(p.u.)	1/2充电电纳(p.u.)	Plmax(p.u.)	Plmin(p.u.)
1	1	2	0.0575	0.0264	1.3	-1.3
2	1	3	0.1852	0.0204	1.3	-1.3
3	2	4	0.1737	0.0184	0.65	-0.65
4	3	4	0.0379	0.0042	1.3	-1.3
5	2	5	0.1983	0.0209	1.3	-1.3
6	2	6	0.1763	0.0187	0.65	-0.65
7	4	6	0.0414	0.0045	0.9	-0.9
8	5	7	0.116	0.0102	0.7	-0.7
9	6	7	0.082	0.0085	1.3	-1.3
10	6	8	0.042	0.0045	0.32	-0.32
11	6	9	0.208	0	0.65	-0.65
12	6	10	0.556	0	0.32	-0.32
13	9	11	0.208	0	0.65	-0.65
14	9	10	0.11	0	0.65	-0.65
15	4	12	0.256	0	0.65	-0.65
16	12	13	0.14	0	0.65	-0.65
17	12	14	0.2559	0	0.32	-0.32
18	12	15	0.1304	0	0.32	-0.32
19	12	16	0.1987	0	0.32	-0.32
20	14	15	0.1997	0	0.16	-0.16
21	16	17	0.1932	0	0.16	-0.16
22	15	18	0.2185	0	0.16	-0.16
23	18	19	0.1292	0	0.16	-0.16
24	19	20	0.068	0	0.32	-0.32
25	10	20	0.209	0	0.32	-0.32
26	10	17	0.0845	0	0.32	-0.32
27	10	21	0.0749	0	0.32	-0.32
28	10	22	0.1499	0	0.32	-0.32
29	21	22	0.0236	0	0.32	-0.32
30	15	23	0.202	0	0.16	-0.16
31	22	24	0.179	0	0.16	-0.16
32	23	24	0.27	0	0.16	-0.16
33	24	25	0.3292	0	0.16	-0.16
34	25	26	0.38	0	0.16	-0.16
35	25	27	0.2087	0	0.16	-0.16
36	28	27	0.396	0	0.65	-0.65
37	27	29	0.4153	0	0.16	-0.16
38	27	30	0.6027	0	0.16	-0.16
39	29	30	0.4533	0	0.16	-0.16
40	8	28	0.2	0.0214	0.32	-0.32
41	6	28	0.0599	0.0065	0.32	-0.32

机组参数：

机组编号	节点号	Pmax(p.u.)	Pmin(p.u.)	a(吨/(p.u.)2）	b(吨/p.u.）	c(吨）	Ru/Rd 上/下爬坡速率 (p.u./h)	TS/TD 关停/开机最小持续时间(h)	H 启动成本($/次)	J 关停成本($/次)
1	1	1.5749	0.5	0.1524	38.5397	786.799	0.375	2	39373	19686
2	2	1	0.25	0.1058	46.1591	945.633	0.3	2	25000	12500
3	5	0.6	0.15	0.028	40.3965	1050	0.15	2	15000	7500
4	8	0.8	0.2	0.0354	38.3055	1243.53	0.2	2	20000	10000
5	11	0.4	0.1	0.0211	36.3278	1658.57	0.15	2	10000	5000
6	13	0.4	0.1	0.0179	38.2704	1356.66	0.15	2	10000	5000

各节点各时段负荷曲线（24小时）：

节点编号	T1	T2	T3	T4	T5	T6	T7	T8	T9	T10	T11	T12	T13	T14	T15	T16	T17	T18	T19	T20	T21	T22	T23	T24
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0.164080073	0.157628	0.152817	0.151232	0.151232	0.152817	0.175287	0.19453	0.208963	0.210604	0.210604	0.208963	0.208963	0.208963	0.205793	0.207378	0.215132	0.217	0.217	0.210604	0.202511	0.189719	0.173702	0.157628
3	0.018147105	0.017433	0.016901	0.016726	0.016726	0.016901	0.019387	0.021515	0.023111	0.023293	0.023293	0.023111	0.023111	0.023111	0.022761	0.022936	0.023793	0.024	0.024	0.023293	0.022397	0.020983	0.019211	0.017433
4	0.057465832	0.055206	0.053521	0.052966	0.052966	0.053521	0.061391	0.06813	0.073185	0.07376	0.07376	0.073185	0.073185	0.073185	0.072075	0.07263	0.075346	0.076	0.076	0.07376	0.070925	0.066445	0.060836	0.055206
5	0.712273866	0.684264	0.66338	0.656501	0.656501	0.66338	0.760922	0.844459	0.907111	0.914236	0.914236	0.907111	0.907111	0.907111	0.893352	0.900232	0.933892	0.942	0.942	0.914236	0.879102	0.823574	0.754042	0.684264
6	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
7	0.172397496	0.165618	0.160563	0.158898	0.158898	0.160563	0.184172	0.204391	0.219556	0.22128	0.22128	0.219556	0.219556	0.219556	0.216225	0.21789	0.226038	0.228	0.228	0.22128	0.212776	0.199336	0.182507	0.165618
8	0.226838811	0.217919	0.211268	0.209077	0.209077	0.211268	0.242332	0.268936	0.288889	0.291158	0.291158	0.288889	0.288889	0.288889	0.284507	0.286698	0.297418	0.3	0.3	0.291158	0.279969	0.262285	0.240141	0.217919
9	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
10	0.043855503	0.042131	0.040845	0.040421	0.040421	0.040845	0.046851	0.051994	0.055852	0.056291	0.056291	0.055852	0.055852	0.055852	0.055005	0.055428	0.057501	0.058	0.058	0.056291	0.054127	0.050708	0.046427	0.042131
11	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
12	0.084686489	0.081356	0.078873	0.078055	0.078055	0.078873	0.090471	0.100403	0.107852	0.108699	0.108699	0.107852	0.107852	0.107852	0.106216	0.107034	0.111036	0.112	0.112	0.108699	0.104522	0.09792	0.089653	0.081356
13	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
14	0.046880021	0.045037	0.043662	0.043209	0.043209	0.043662	0.050082	0.05558	0.059704	0.060173	0.060173	0.059704	0.059704	0.059704	0.058798	0.059251	0.061466	0.062	0.062	0.060173	0.05786	0.054206	0.049629	0.045037
15	0.062002608	0.059564	0.057746	0.057148	0.057148	0.057746	0.066237	0.073509	0.078963	0.079583	0.079583	0.078963	0.078963	0.078963	0.077765	0.078364	0.081294	0.082	0.082	0.079583	0.076525	0.071691	0.065638	0.059564
16	0.026464528	0.025424	0.024648	0.024392	0.024392	0.024648	0.028272	0.031376	0.033704	0.033968	0.033968	0.033704	0.033704	0.033704	0.033192	0.033448	0.034699	0.035	0.035	0.033968	0.032663	0.0306	0.028016	0.025424
17	0.068051643	0.065376	0.06338	0.062723	0.062723	0.06338	0.0727	0.080681	0.086667	0.087347	0.087347	0.086667	0.086667	0.086667	0.085352	0.086009	0.089225	0.09	0.09	0.087347	0.083991	0.078685	0.072042	0.065376
18	0.02419614	0.023245	0.022535	0.022302	0.022302	0.022535	0.025849	0.028686	0.030815	0.031057	0.031057	0.030815	0.030815	0.030815	0.030347	0.030581	0.031725	0.032	0.032	0.031057	0.029863	0.027977	0.025615	0.023245
19	0.07183229	0.069008	0.066901	0.066208	0.066208	0.066901	0.076738	0.085163	0.091481	0.0922	0.0922	0.091481	0.091481	0.091481	0.090094	0.090788	0.094182	0.095	0.095	0.0922	0.088657	0.083057	0.076045	0.069008
20	0.016634846	0.015981	0.015493	0.015332	0.015332	0.015493	0.017771	0.019722	0.021185	0.021352	0.021352	0.021185	0.021185	0.021185	0.020864	0.021025	0.021811	0.022	0.022	0.021352	0.020531	0.019234	0.01761	0.015981
21	0.13232264	0.127119	0.123239	0.121961	0.121961	0.123239	0.14136	0.156879	0.168519	0.169842	0.169842	0.168519	0.168519	0.168519	0.165962	0.16724	0.173494	0.175	0.175	0.169842	0.163315	0.152999	0.140082	0.127119
22	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
23	0.02419614	0.023245	0.022535	0.022302	0.022302	0.022535	0.025849	0.028686	0.030815	0.031057	0.031057	0.030815	0.030815	0.030815	0.030347	0.030581	0.031725	0.032	0.032	0.031057	0.029863	0.027977	0.025615	0.023245
24	0.065783255	0.063196	0.061268	0.060632	0.060632	0.061268	0.070276	0.077991	0.083778	0.084436	0.084436	0.083778	0.083778	0.083778	0.082507	0.083142	0.086251	0.087	0.087	0.084436	0.081191	0.076063	0.069641	0.063196
25	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
26	0.026464528	0.025424	0.024648	0.024392	0.024392	0.024648	0.028272	0.031376	0.033704	0.033968	0.033968	0.033704	0.033704	0.033704	0.033192	0.033448	0.034699	0.035	0.035	0.033968	0.032663	0.0306	0.028016	0.025424
27	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
28	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
29	0.018147105	0.017433	0.016901	0.016726	0.016726	0.016901	0.019387	0.021515	0.023111	0.023293	0.023293	0.023111	0.023111	0.023111	0.022761	0.022936	0.023793	0.024	0.024	0.023293	0.022397	0.020983	0.019211	0.017433
30	0.080149713	0.076998	0.074648	0.073874	0.073874	0.074648	0.085624	0.095024	0.102074	0.102876	0.102876	0.102074	0.102074	0.102074	0.100526	0.1013	0.105088	0.106	0.106	0.102876	0.098922	0.092674	0.08485	0.076998
总负荷	2.142870632	2.058605	1.995775	1.975078	1.975078	1.995775	2.289227	2.540547	2.729037	2.750473	2.750473	2.729037	2.729037	2.729037	2.687643	2.70834	2.809607	2.834	2.834	2.750473	2.644771	2.477717	2.268531	2.058605

注意：数据均基于标幺化系统得到，因此电力电量参数、网络参数等都为标幺值，无量纲。还要注意附件中煤耗系数a,b,c的单位为吨，因此计算煤耗成本还需换算为价格，设燃煤价格为100$/吨。

求解：机组组合结果，即机组各时段启停计划、机组各时段最优出力，以及内含的各时段的直流潮流等。

代码

clear;
clc;
yalmip;
Cplex;
%%系统参数
%所有参数均用有名值表示
paragen=xlsread('excel2017','机组参数');
loadcurve=xlsread('excel2017','负荷曲线');
netpara=xlsread('excel2017','网络参数');
branch_num=size(netpara);%网络中的支路
branch_num=branch_num(1,1);
PL_max=netpara(:,6);%线路最大负荷
PL_min=netpara(:,7);%线路最小负荷
limit=paragen(:,3:4);%机组出力上下限//limit(:,1)表示上限，limit(:,2)表示下限
para=paragen(:,5:7);%成本系数//para(:,1)表示系数a,para(:,2)表示系数b,para(:,3)表示系数c。
price=100;
para=price*para;%价格换算
lasttime=paragen(:,9);%持续时间
Rud=paragen(:,8);%上下爬坡速率//因题中简化上坡下坡速度相同
H=paragen(:,10);%启动成本
J=paragen(:,11);%关停成本
u0=[1 1 1 1 1 1];%初始状态
%% 规模变量
%机组数
gennum=size(paragen);
gennum=gennum(1,1);
%节点数
numnodes=size(loadcurve);
numnodes=numnodes(1,1)-1;
%时间范围
T=size(loadcurve);
T=T(1,2)-1;
%线性化分段数(按需要更改)
m=4;
%各时刻节点总负荷
PL=loadcurve(numnodes+1,2:T+1);
%%
%决策变量
u=binvar(gennum,T,'full');%状态变量
p=sdpvar(gennum,T,'full');%即各机组实时功率p(i,t)
Ps=sdpvar(gennum,T,m,'full');%分段出力
costH=sdpvar(gennum,T,'full');%启动成本
costJ=sdpvar(gennum,T,'full');%关停成本
sum_PowerGSDF=sdpvar(T,branch_num,numnodes,'full');%发电机的输出功率转移总和
%% 目标函数线性化
MaxPs=zeros(gennum,T,m);%这里表示分段出力的上限
st=[];%st约束初始化
for i=1:gennum   %目标函数线性化后分段出力的不等式约束
   for t=1:T
     for s=1:m
	MaxPs(i,t,s)=(limit(i,1)-limit(i,2))/m;
    st=st+[Ps(i,t,s)>=0,Ps(i,t,s)<=MaxPs(i,t,s)];
     end
   end
end
K=zeros(gennum,m);%煤耗函数的斜率值
for i=1:gennum
    for s=1:m
        K(i,s)=2*para(i,1)*(2*s-1)*MaxPs(i,1,1)+para(i,2);%推导简化后的煤耗斜率
    end
end
 %目标函数线性化后分段出力的等式约束
for i=1:gennum 
    for t=1:T
st=st+[p(i,t)==(sum(Ps(i,t,:),3)+u(i,t)*limit(i,2))];
    end
end
%% 目标函数
totalcost=0;%机组费用成本最小
%线性化的最优成本目标
for i=1:gennum
    for t=1:T
        for s=1:m
            totalcost=totalcost+K(i,s)*Ps(i,t,s);%线性化煤耗成本
        end
        totalcost=totalcost+u(i,t)*(para(i,2)*limit(i,2)+para(i,1)*limit(i,2)^2+para(i,3));%加上表示机组开机并以最小出力 运行产生的煤耗
        totalcost=totalcost+costH(i,t)+costJ(i,t);%加上机组启停产生的开停机成本
    end
end
%原二次函数式的最优成本目标
% for i=1:gennum
%     for t=1:T
%     totalcost=totalcost+para(i,1)*p(i,t).^2+para(i,2)*p(i,t)+para(i,3)*u(i,t);  %煤耗成本
%     totalcost=totalcost+costH(i,t);                                %启动成本
%     totalcost=totalcost+costJ(i,t);                                %关停成本
%     end
% end
%%
for t=1:T
st=st+[sum(p(:,t))==PL(1,t)];%负荷平衡约束;
end
%%
for t=1:T
    for i=1:gennum
  st=st+[u(i,t)*limit(i,2)<=p(i,t)<=u(i,t)*limit(i,1)];%机组出力上下限约束
    end
end
%% 机组爬坡约束
%按下式进行推导编程
% %启动最大升速率
% Su=(Pmax+Pmin)/2;
% %停机最大降速率
% Sd=(Pmax+Pmin)/2;
%Ru=Rud;Rd=Rud;
% %上爬坡约束
% for t=2:T
% st=st+[p(:,t)-p(:,t-1)<=u(:,t-1).*(Ru-Su)+Su];
% end
% %下爬坡约束
% for t=2:T
%st=st+[p(:,t-1)-p(:,t)<=u(:,t).*(Rd-Sd)+Sd];
% end
%展开表达式：
for t=2:T
    for i=1:gennum
    % st=st+[-Rud(i,1)*u(i,t)+(u(i,t)-u(i,t-1))*limit(i,2)-limit(i,1)*(1-u(i,t))<=p(i,t)-p(i,t-1)];
    % st=st+[p(i,t)-p(i,t-1)<=Rud(i,1)*u(i,t-1)+(u(i,t)-u(i,t-1))*limit(i,2)+limit(i,1)*(1-u(i,t))];
    %由于原式可能关机以后就无法再开动了，改用下式
    st=st+[p(i,t-1)-p(i,t)<=Rud(i,1)*u(i,t)+(1-u(i,t))*(limit(i,2)+limit(i,1))/2];%下坡
    st=st+[p(i,t)-p(i,t-1)<=Rud(i,1)*u(i,t-1)+(1-u(i,t-1))*(limit(i,2)+limit(i,1))/2];%上坡
    end
end
%% 热备用约束
hp=0.05;%热备用系数
for t=1:T
st=st+[sum(u(:,t).*limit(:,1)-p(:,t))>=hp*PL(1,t)];
end
%% 启停时间约束
%启动约束
for t=2:T
    for i=1:gennum
        indicator=u(i,t)-u(i,t-1);%启停时间约束的简化表达式（自己推导的）,indicator为1表示启动，为0表示停止
        range=t:min(T,t+lasttime(i)-1);
        st=st+[u(i,range)>=indicator];
    end
end
%停机约束
for t=2:T
    for i=1:gennum
        indicator=u(i,t-1)-u(i,t);%启停时间约束
        range=t:min(T,t+lasttime(i)-1);%特别限制时间上限
        st=st+[u(i,range)<=1-indicator];
    end
end
%% 启停成本约束
for t=1:T   %启停成本零限约束
    for i=1:gennum
        st=st+[costH(i,t)>=0]; 
        st=st+[costJ(i,t)>=0];
    end
end
for i=1:gennum  %启停成本条件约束
   for t=2:T
         st=st+[costH(i,t)>=H(i,1)*(u(i,t)-u(i,t-1))];
         st=st+[costJ(i,t)>=J(i,1)*(u(i,t-1)-u(i,t))];
   end
    st=st+[costH(i,1)>=H(i,1)*(u(i,1)-u0(1,i))];%初始状态下的启停成本
    st=st+[costJ(i,1)>=J(i,1)*(u0(1,i)-u(i,1))];
end
%% 直流潮流约束
%% 直流潮流下的导纳矩阵节点参数初始化
netpara(:,4)=1./netpara(:,4);%电抗求倒数成电纳
slack_bus=26;%按不同的平衡节点号更改
Y=zeros(numnodes,numnodes);
%% 直流潮流的导纳矩阵计算
for k=1:branch_num 
    i=netpara(k,2);%首节点
    j=netpara(k,3);%尾节点
    Y(i,j)=-netpara(k,4);%导纳矩阵中非对角元素
    Y(j,i)= Y(i,j);
end
for k=1:numnodes
       Y(k,k)=-sum(Y(k,:)); %导纳矩阵中的对角元素 
end
%再删除掉平衡节点所在的行与列
Y(slack_bus,:)=[];
Y(:,slack_bus)=[];
xlswrite('直流潮流下的节点导纳矩阵',Y,'平衡节点取在第26号节点');
%% 输出功率转移分布因子(GSDF)
X=inv(Y);%X为直流潮流下节点导纳矩阵的逆矩阵
xlswrite('节点导纳的逆矩阵',X,'平衡节点未补充');
row=zeros(1,numnodes-1);%numnodes-1是因为节点导纳矩阵去掉了平衡节点
%再次引入平衡节点的矩阵值，根据直流潮流定义ΔΘ=ΧΔP,平衡机角度始终为0，所以所有涉及平衡节点的X均为0
X=[X(1:slack_bus-1,:);row;X(slack_bus:numnodes-1,:)];%插入全0行
column=zeros(numnodes,1);
X=[X(:,1:slack_bus-1) column X(:,slack_bus:numnodes-1)];%插入全0列
xlswrite('节点导纳的逆矩阵',X,'平衡节点补充');
G=zeros(branch_num,numnodes);%GSDF功率转移矩阵初始化
for k=1:branch_num
    m=netpara(k,2);%首端节点
    n=netpara(k,3);%末端节点
    xk=netpara(k,4);%支路k的阻抗值
for i=1:numnodes
    G(k,i)=(X(m,i)-X(n,i))*xk;%输出功率转移分布因子
end
end
power_gen=paragen(:,2);%发电机对应节点
sum_nodeGSDF=zeros(T,branch_num);%负荷节点的输出功率转移
for t=1:T
    for k=1:branch_num
        for i=1:gennum
            sum_PowerGSDF(t,k,i)=G(k,power_gen(i,1))*p(i,t);%这里即发电机对线路的输出功率转移式
        end
        for i=1:numnodes
            sum_nodeGSDF(t,k)=sum_nodeGSDF(t,k)+G(k,i)*loadcurve(i,t+1);%这里是所有负荷节点对线路的输出功率转移式
        end
        st=st+[PL_min(k,1)<=(sum(sum_PowerGSDF(t,k,:))-sum_nodeGSDF(t,k))];
        st=st+[(sum(sum_PowerGSDF(t,k,:))-sum_nodeGSDF(t,k))<=PL_max(k,1)];
    end
end
%% 求解
ops=sdpsettings('solver', 'cplex');
result=solvesdp(st,totalcost);
double(totalcost) 
subplot(1,2,1)
bar(value(p)','stack')%阶梯图
legend('Unit 1','Unit 2','Unit 3','Unit 4','Unit 5','Unit 6');	%在坐标轴上添加图例
subplot(1,2,2)
stairs(value(p)')
legend('Unit 1','Unit 2','Unit 3','Unit 4','Unit 5','Unit 6');	%在坐标轴上添加图例
xlswrite('机组组合问题求解结果',double(u),'机组各时段启停计划');
P=(sum(sum_PowerGSDF(:,:,:),3)-sum_nodeGSDF(:,:))';%各段支路的实时潮流
P_sp=zeros(numnodes,T);%各个节点的直流潮流功率
for i=1:numnodes
for k=1:branch_num
    m=netpara(k,2);%首端节点
    n=netpara(k,3);%末端节点
    if m==i
        P_sp(i,:)=P_sp(i,:)+P(k,:);
    end
    if n==i
        P_sp(i,:)=P_sp(i,:)-P(k,:);
    end
end
end
dot_theta=zeros(numnodes,T);
dot_theta=X*P_sp;       
xlswrite('机组组合问题求解结果',double(P),'支路各时段的直流潮流');
xlswrite('机组组合问题求解结果',double(P_sp),'节点各时段的潮流功率');
xlswrite('机组组合问题求解结果',double(dot_theta),'节点各时段的潮流相角');


set(0,'ShowHiddenHandles','On')
set(gcf,'menubar','figure')