外排序与MapReduce的Sort

外排序与MapReduce的Sort数据结构课设——外排序Visual Studio 2019Qt Creator4.9C++代码地址：DataStructureCourseProject/ExternalSort(Qt+Vs) at main · Tcoder-l3est/DataStructureCourseProject (github.com)基础数据结构使用竞赛树—最小书输者树来实现外排

Tcoder-l3est

2812人浏览 · 2022-04-06 21:08:40

Tcoder-l3est · 2022-04-06 21:08:40 发布

外排序与MapReduce的Sort

数据结构课设——外排序

Visual Studio 2019

Qt Creator4.9

C++

代码地址：DataStructureCourseProject/ExternalSort(Qt+Vs) at main · Tcoder-l3est/DataStructureCourseProject (github.com)

基础数据结构

使用竞赛树—最小书输者树来实现外排序的归并串的K路归并最终得到排序文件

基础要求

设计并实现最小输者树结构 ADT，ADT 中应包括初始化、返回赢者，重构

等基本操作。

应用最小输者树设计实现外排序，外部排序中的生成最初归并串以及 K 路

归并都应用最小输者树结构实现；

随机创建一个较长的文件作为外排序的初始数据；设置归并路数以及缓冲区

的大小；获得外排序的访问磁盘的次数并进行分析。可采用小文件来模拟磁

盘块。

基本步骤

部分排序生成顺串
顺串进行归并(可能多次可能多路归并)

最小输者树

首先定义Player结构体，包括元素值以及串号，重载运算符

struct Player
{//选手
	int element;//元素值 
	int num;//顺串号
	//bool operator<(const Player &p1)
	//{//先看顺串号再看元素
	//	return (num != p1.num) ? (num < p1.num) : (element < p1.element);
	//}
	bool operator<=(const Player& p1)
	{//先看顺串号再看元素
		return (num != p1.num) ? (num < p1.num) : (element < p1.element);
	}
	Player& operator=(const Player& p)
	{
		num = p.num;
		element = p.element;
		return *this;
	}
	friend ostream& operator<<(ostream& out, Player& p) {
		out << p.element;
		return out;
	};
};

定义最小输者树类


template<class T>
class minLoserTree
{
public:
	minLoserTree(T* ThePlayers = NULL, int n = 0);
	~minLoserTree() { delete[] tree; delete[] edges; }

	void initialize(T* thePlayer,
		int theNumberOfPlayers);
	void play_once(int p, int leftChild, int rightChild);
	int winner(int x, int y) //返回更小的元素下标
	{ //winner 入边 
		return players[x] <= players[y] ? x : y;
	};
	int loser(int x, int y)//返回更大的元素下标
	{//loser 入内部节点
		return players[x] <= players[y] ? y : x;
	};
	void replay(int thePlayer);//重构
	void output();
	void maintain() { tree[0] = edges[1]; };//维护tree[0]
	long long int top() {//返回最小的tree[0]
		return tree[0];
	};
	void make_run(fstream& fin);
	void merge_K(int k, int sta, int level);
	void get_total() {
		totals = 0;
		if (max_run % kk == 0) {
			int temp = max_run / kk; totals += temp;
			while (temp != 1)
			{
				temp /= kk;
				totals += temp;
			}
		}
		else
		{
			int temp = max_run / kk; totals += temp; totals++;
			while (temp != 0)
			{
				temp /= kk;
				totals += temp;
				totals++;
			}
		}
	};
	int kk;				  // K
private:
	T* players;//元素数组
	int* edges;//边上的晋级的元素
	int numberofPlayers;//总共多少参赛者
	int* tree;//专门记录内部节点，tree[0]用来记录最后的输者
	int lowExt;           // lowest-level external nodes
	int offset;           // 2^log(n-1) - 1
	int totals = 0;           //K路合并总共多少 S

};

首先是私有成员：player是存具体元素的(Player 结构体)
edges是需要记录输者树边的信息，边上的信息是记录的晋级的元素，也就是赢的元素，大的元素
t是记录树的内部节点，存的是顺串号
lowExt 是最底层叶子叶节点的位置
offset 是用来看每一层多少节点的

拓展之模拟磁盘

结构体Page

//缓冲区 
struct Page {
	long int* arr;
	int position; //当前顺串扫描的位置 
	Page() {
		position = 0;
	}
	Page(int page_size) {
		position = 0;
		arr = new long int[page_size + 1];
	}
};

主要用在K路归并的函数里面

其实是复杂化了，就是有个输出缓冲区，由Page构成，每次先输入到缓冲区里面，到缓冲区满了就写入到磁盘，也就是真是的文件，然后清空缓冲区。

其中还得考虑一些模拟指针等等问题

我实现的貌似还有小BUG~

其他

自己创建数据集，这个很简单了就是随机数~

设计思路

输者树数据结构相关

voidminLoserTree<T>::initialize(T* thePlayer, int theNumberOfPlayers)设计思路

进行最小输者树的初始化，根据传入的数组，计算得出最底层外部节点个数，单独处理之后，再对上一层进行处理（比赛一次），如果是奇数个，则需要特殊处理。之后进行play_once()
void minLoserTree<T>::play_once(int p, int leftChild, int rightChild)设计思路

根据传入的左右孩子，先进行左右孩子的比赛，并且输者放在tree树结构中，赢者放在边结构中，之后，只要没到根节点，就一直比赛，循环构建好整棵树。
void minLoserTree<T>::replay(int thePlayer)设计思路：

首先根据被替换掉的选手的索引，判断是最外层节点，还是上一层的节点，然后对于从此节点到根的比赛，进行重比，即完成了重构， $O(\log(n))$

外排序相关

void minLoserTree<T>::make_run(fstream& fin)的设计思路

进行生成顺串的操作。

首先从文件、外存中读入输入缓存区大小的文件。

之后进行根据输入的元素进行内部排序，使用最小输者树进行，方法为：输入P个元素初始化一个最小输者树，顺串号都为1，之后将树顶，即最小的元素W加入到输出缓冲区中，然后，用新的元素N替代最小元素，如果新输入的<输出的，则N的顺串号=W顺串号+1，否则N顺串号=W顺串号，N代替W，重构输者树；

一直进行，如果输出满了就输出到外存。直到外存中所有元素都完成顺串的生成。
void minLoserTree::merge_K(int k, int sta, int level)的设计思路

K路归并

对生成的顺串进行K路合并：

因为K可以随机指定，不是固定为顺串数目，所以合并树可能是多层。

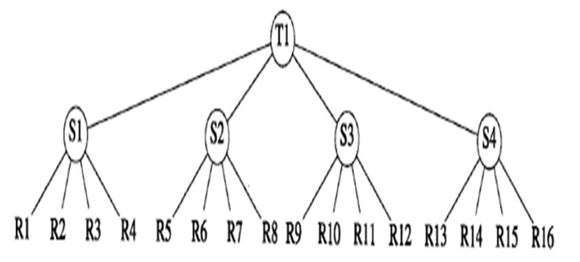
首先：需要确定层数，如果是顺串层，则需要读入顺串，然后生成中间的合并的文件Si，之后对于S层需要再向上进行K路合并，一直到最后只剩下一个S为止，也就是最终排序好的文件T。

所以上述过程是一个迭代过程，确定好每次迭代量：即合并的文件，生成的文件，进行K路合并即可。

而具体K路合并过程：根据当前需要合并的文件数目K，建立K个选手组成的最小输者树，然后对应每个文件，输入元素，进行建树，之后输出最小的元素，再用下一个元素代替他，重构，直到每个文件都处理完，把输出存到一个新文件中。

磁盘模拟相关

Page* make_in_Buffer(int now_k)设计思路

生成一个输入缓冲区，每次根据当前的合并的顺串数目进行K路合并。所以需要用每次新建一个page类型的数组，用来模拟分页式缓存区。

由上述可知：

需要自定义struct Page类型，作为页，即缓存区为 Page数组，每一个数组元素都是一页，并且需要加一个位置指针position，来记录读写到的位置。
void disk_in_buffer(int now_k, ifstream* fins, Page* inBuffer)思路

从磁盘输入模拟缓存区，只需要打开文件然后把缓存区输满，或者把文件输空。

void buffer_to_disk(int outpoint,ofstream &fout, vector<long> outBuffer)函数的设计思路

如果输出缓冲区已经满了，此时需要调用该函数，把缓冲区的数据输入到磁盘中，访问一次磁盘，并且清空缓存区（或者直接覆盖）

利用PAGE数组，因为磁盘文件可能是多个，所以传入的是ifstream输入流数组，进行多个文件的输入，并且写到inbuffer中。

思考

进行大数据测试时，排序时间较长,有时甚至能长达10+min

解决：

多线程外排序解决大数据排序问题(并行内排和并行归并)

并行内排：

采用分区的思想，同时启动多个外排序程序用来生成顺串，固定区大小，例如排1e6 每次读入1e5个数据，所以开启十个进程，分别读外存的0-1e5 1e5-2e5 2e5-3e5 ··· 9e5-1e6 同时进行，则可以以原来十分之一的速度生成所有的顺串。

并行归并：

多个线程单独对两两顺串进行合并，直到剩下一个。

上述在不严谨的模拟下，大文件排序可以缩短4-5倍。
究竟为什么使用最小输者树，可以减少顺串个数？

回答：

读入新的数据，比原来的小顺串号++ 大则不加

一开始的输入时 sizeof_inbuffer个player sizeofile(文件大小，假设为10000) / INbuffer(输入缓冲区大小假设为1000) =N,假设此时为10

1000个元素，一定有一个最小值，他们都会输出到顺串1，

最差情况后面重构是每次都小一点点则后面也是最多N-1个

则最多是N个顺串！！！

最好的情况则是如果是有序的那么就只有一个顺串！！！直接有序！

而只要前面数字有比较小的则必然小于这个N

而N则是其他排序方法的固定的顺串数目！

随机数据的话根据概率应该在中间附近所以平均顺串数目应该是N/2

顺串的平均长度也比一般的内排序方法长，大概为2*players

总之，动态确定顺串号，比其他排序有天然的有时，减少了一半的顺串数！
为什么用输者树不用赢者树？

回答：

排序需要不断重构树结构，输者树向上重构，只需要比较自己和父节点的大小就可以了，而赢者树需要看兄弟节点的大小，访存代价大。所以使用输者树是一个更优的选择！
归并的拓展

借鉴霍夫曼树的思路，如果先合并的顺串长度最长，那么，在合并树中他出现的次数会比其他的多，代价会更高。所以记录每个顺串的长度，从最短的顺串开始合并。效率会更高。
外排序所需要的时间=内排序所需的时间+外存读写所需时间+内归并所需时间，减少外存信息的读写次数是提高外部排序效率的关键。

而对于同一个文件来说，进行外排序所需读写外存的次数与归并趟数有关，为了减少归并趟数，可以通过减少初始顺串的个数、增加归并的路数两个方面进行。