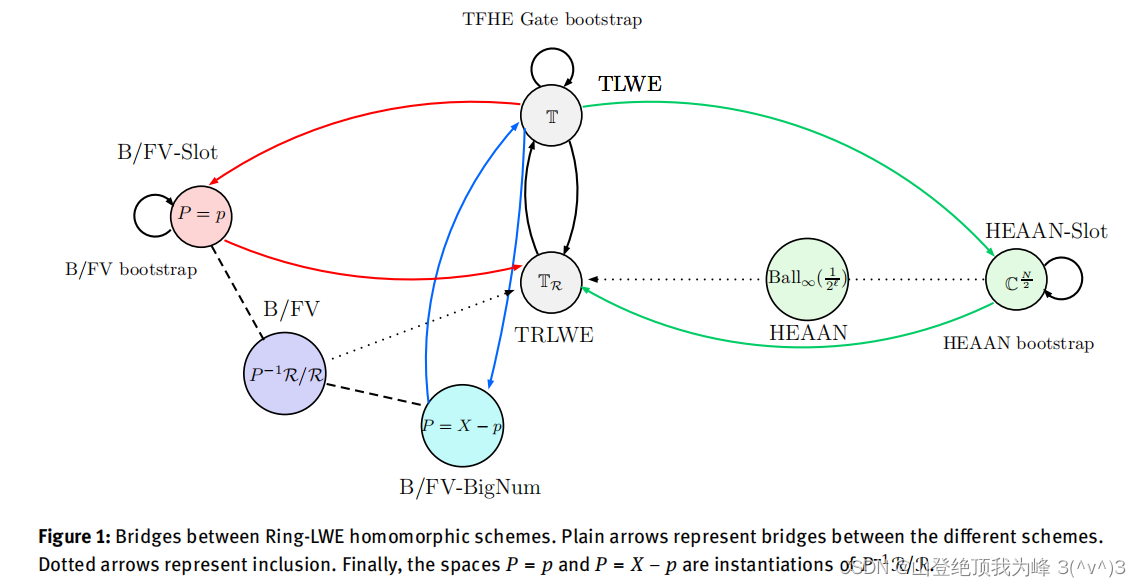
Chimera:混合的 RLWE-FHE 方案
[CGGI20] 给出了实数环面(Torus)上的 T( R )LWE-based FHE 算法 TFHE,其密文的底层代数结构是连续的环面(而非 BGV/BFV、CKKS 的离散的环)。[BGGJ20] 提出了如何把 BFV、CKKS 的明密文空间都映射到环面上,**可以将 BFV、CKKS、TFHE 的明密文空间统一起来**,实现了三者之间的密文转换。开源代码:[DPPH/**chimera-
参考文献:
- [AP13] Alperin-Sheriff J, Peikert C. Practical bootstrapping in quasilinear time[C]//Annual Cryptology Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 1-20.
- [HS14] S. Halevi and V. Shoup. Algorithms in HElib. In Advances in Cryptology–CRYPTO 2014, pages 554–571. Springer, 2014.
- [HS15] S. Halevi and V. Shoup. Bootstrapping for HElib. In Advances in Cryptology–EUROCRYPT 2015, pages 641–670. Springer, 2015.
- [CHKKS18] Cheon J H, Han K, Kim A, et al. Bootstrapping for approximate homomorphic encryption[C]//Advances in Cryptology–EUROCRYPT 2018: 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, April 29-May 3, 2018 Proceedings, Part I 37. Springer International Publishing, 2018: 360-384.
- [CGGI20] Chillotti I, Gama N, Georgieva M, et al. TFHE: fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34-91.
- [BGGJ20] Boura C, Gama N, Georgieva M, et al. Chimera: Combining ring-lwe-based fully homomorphic encryption schemes[J]. Journal of Mathematical Cryptology, 2020, 14(1): 316-338.
- [MP21] Micciancio D, Polyakov Y. Bootstrapping in FHEW-like cryptosystems[C]//Proceedings of the 9th on Workshop on Encrypted Computing & Applied Homomorphic Cryptography. 2021: 17-28.
- [LHH+21] Lu W, Huang Z, Hong C, et al. PEGASUS: bridging polynomial and non-polynomial evaluations in homomorphic encryption[C]//2021 IEEE Symposium on Security and Privacy (SP). IEEE, 2021: 1057-1073.
- [ABB+22] Al Badawi A, Bates J, Bergamaschi F, et al. Openfhe: Open-source fully homomorphic encryption library[C]//Proceedings of the 10th Workshop on Encrypted Computing & Applied Homomorphic Cryptography. 2022: 53-63.
- TFHE 的全同态模结构(FHE Module Structure)-CSDN博客
文章目录
Switching between BGV and BFV
根据 [AP13],LSB 编码与 MSB 编码之间的转换是容易的,因此在 BGV 和 BFV 之间的 Scheme Switching 是平凡的。
明文模数
p
p
p,密文模数
q
q
q,假设
g
c
d
(
p
,
q
)
=
1
gcd(p,q)=1
gcd(p,q)=1,那么根据扩展欧几里得算法得到
c
p
p
+
c
q
q
=
1
c_pp+c_qq=1
cpp+cqq=1,这里
c
p
=
p
−
1
(
m
o
d
q
)
,
c
q
=
q
−
1
(
m
o
d
p
)
c_p = p^{-1} \pmod{q},\,\, c_q = q^{-1} \pmod{p}
cp=p−1(modq),cq=q−1(modp)
- LSB 编码:明文 μ ∈ Z p \mu \in \mathbb Z_p μ∈Zp,编码值 v ∈ Z q v \in \mathbb Z_q v∈Zq 满足 v = e ( m o d q ) v = e \pmod{q} v=e(modq),其中 e ∈ { μ + p Z } ∩ [ − q / 2 , q / 2 ) e \in \{\mu + p\mathbb Z\} \cap [-q/2,q/2) e∈{μ+pZ}∩[−q/2,q/2)
- MSB 编码:明文 μ ∈ Z p \mu \in \mathbb Z_p μ∈Zp,编码值 w ∈ Z q w \in \mathbb Z_q w∈Zq 满足 ⌊ w ⌉ p = μ ( m o d p ) \lfloor w \rceil_p = \mu \pmod{p} ⌊w⌉p=μ(modp),其中 ⌊ w ⌉ p : = ⌊ w ⋅ ( p / q ) ⌉ \lfloor w \rceil_p := \lfloor w \cdot (p/q) \rceil ⌊w⌉p:=⌊w⋅(p/q)⌉
从 LSB 到 MSB 的转换:给定
μ
∈
Z
p
\mu \in \mathbb Z_p
μ∈Zp 的 LSB 编码
v
∈
Z
q
v \in \mathbb Z_q
v∈Zq,计算
w
=
p
−
1
⋅
v
(
m
o
d
q
)
w=p^{-1} \cdot v \pmod{q}
w=p−1⋅v(modq),它就是
−
q
−
1
⋅
μ
∈
Z
p
-q^{-1}\cdot \mu \in \mathbb Z_p
−q−1⋅μ∈Zp 的 MSB 编码值。容易验证:
⌊
p
−
1
⋅
v
⌉
p
=
⌊
p
−
1
⋅
e
⋅
p
q
⌉
=
⌊
1
−
c
q
q
p
⋅
e
⋅
p
q
⌉
=
⌊
(
1
q
−
c
q
)
⋅
e
⌉
=
−
c
q
⋅
e
=
−
q
−
1
⋅
μ
(
m
o
d
p
)
\begin{aligned} \lfloor p^{-1} \cdot v \rceil_p &= \left\lfloor p^{-1} \cdot e \cdot \dfrac{p}{q} \right\rceil\\ &= \left\lfloor \dfrac{1-c_qq}{p} \cdot e \cdot \dfrac{p}{q} \right\rceil\\ &= \left\lfloor (\dfrac{1}{q}-c_q) \cdot e \right\rceil\\ &= -c_q \cdot e\\ &= -q^{-1} \cdot \mu \pmod{p} \end{aligned}
⌊p−1⋅v⌉p=⌊p−1⋅e⋅qp⌉=⌊p1−cqq⋅e⋅qp⌉=⌊(q1−cq)⋅e⌉=−cq⋅e=−q−1⋅μ(modp)
从 MSB 到 LSB 的转换:给定
μ
∈
Z
p
\mu \in \mathbb Z_p
μ∈Zp 的 MSB 编码
w
∈
Z
q
w \in \mathbb Z_q
w∈Zq,计算
v
=
p
⋅
w
(
m
o
d
q
)
v=p \cdot w \pmod{q}
v=p⋅w(modq),它就是
−
q
⋅
μ
∈
Z
p
-q\cdot \mu \in \mathbb Z_p
−q⋅μ∈Zp 的 LSB 编码值。容易验证:
⌊
w
⌉
p
=
⌊
w
⋅
p
q
⌉
=
w
⋅
p
q
−
e
r
o
u
n
d
=
μ
(
m
o
d
p
)
w
⋅
p
−
q
⋅
e
r
o
u
n
d
=
q
⋅
μ
(
m
o
d
p
q
)
\begin{aligned} \lfloor w \rceil_p = \left\lfloor w \cdot \dfrac{p}{q} \right\rceil = w \cdot \dfrac{p}{q} - e_{round} = \mu \pmod{p}\\ w \cdot p - q \cdot e_{round} = q \cdot \mu \pmod{pq}\\ \end{aligned}
⌊w⌉p=⌊w⋅qp⌉=w⋅qp−eround=μ(modp)w⋅p−q⋅eround=q⋅μ(modpq)
其中 e r o u n d ∈ q − 1 Z ∩ [ − 0.5 , 0.5 ) e_{round} \in q^{-1}\mathbb Z \cap [-0.5,0.5) eround∈q−1Z∩[−0.5,0.5),我们简记 e = q ⋅ e r o u n d ∈ Z q e=q \cdot e_{round} \in \mathbb Z_q e=q⋅eround∈Zq。根据模数 p q pq pq 的整除性,得到了 v = w ⋅ p = e ( m o d q ) v=w \cdot p = e \pmod{q} v=w⋅p=e(modq) 以及 e = − q ⋅ μ ( m o d q ) e = -q \cdot \mu \pmod{q} e=−q⋅μ(modq)
特别地,如果我们设置 q = − 1 ( m o d p ) q = -1 \pmod{p} q=−1(modp),那么就有 q − 1 = − 1 ( m o d p ) q^{-1} = -1 \pmod{p} q−1=−1(modp),此时: p − 1 v = M S B . E n c o d e ( μ ) p^{-1}v=MSB.Encode(\mu) p−1v=MSB.Encode(μ) 以及 p ⋅ w = L S B . E n c o d e ( μ ) p \cdot w = LSB.Encode(\mu) p⋅w=LSB.Encode(μ),恰好就是同一个消息的编码值。而对于其他的 p , q p,q p,q 参数,只要追踪 scale factors − q − 1 -q^{-1} −q−1 和 − q -q −q (的运算),解密时把它们去除即可。或者做关于 − q , − c q ( m o d p ) -q, -c_q \pmod{p} −q,−cq(modp) 的同态线性运算,把 scale factors 消除掉。
Switching between FHEW and TFHE
[MP21] 这两个方案的唯一区别就是自举过程(TFHE 的所有优化技术,包括外积运算等,都可以应用到 FHEW 上):
- AP / FHEW 对密文 a i = ∑ j a i j B j a_i=\sum_j a_{ij} B^j ai=∑jaijBj 做分解,自举秘钥 B K i j = E ( s i ⋅ B j ) BK_{ij} = E(s_i \cdot B^j) BKij=E(si⋅Bj),适合高斯分布的私钥。
- GINX / TFHE 对私钥 s i = ∑ u ∈ U s i u ⋅ u s_i=\sum_{u \in U} s_{iu} \cdot u si=∑u∈Usiu⋅u 做分解,自举秘钥 B K i j = E ( s i u ) BK_{ij} = E(s_{iu}) BKij=E(siu),适合二元/三元分布的私钥。
我们只需要把 TFHE 的离散环面 q − 1 Z / Z q^{-1}\mathbb Z/\mathbb Z q−1Z/Z 使用整环 Z q \mathbb Z_q Zq 来模拟即可:消息加密在 Simple-LWE 密文中(仅支持 Z 4 \mathbb Z_4 Z4 上的线性运算),使用 Ring-GSW 去实现 AP / GINX 两种不同的自举过程(可执行非线性函数) 。因此在 FHEW、TFHE 之间,无需执行 Scheme Switching。
CKKS Bootstrapping
Trigonometric function
在 [CKKS18] 中,作者仅仅给出了 Level FHE,并没有给出 Prue FHE,因为 CKKS 自身并不支持计算模约简,但是自举过程中的模约简却是必要的。[CHKKS18] 利用 CKKS 支持近似计算的优势,采取三角函数来近似模约简,
S
(
x
)
:
=
q
2
π
sin
(
2
π
q
x
)
≈
F
(
x
)
:
=
[
x
]
q
S(x):=\dfrac{q}{2\pi}\sin(\dfrac{2\pi}{q}x) \approx F(x):=[x]_q
S(x):=2πqsin(q2πx)≈F(x):=[x]q
然后将
sin
\sin
sin 归约到
exp
\exp
exp 的计算上,
E
(
x
)
:
=
q
2
π
exp
(
2
π
i
q
x
)
E(x) := \dfrac{q}{2\pi}\exp\left(\dfrac{2\pi i}{q}x\right)
E(x):=2πqexp(q2πix)
最后提取虚部,获得模约减结果,
S
(
x
)
=
I
m
(
E
(
x
)
)
=
1
2
(
E
(
x
)
−
E
(
−
x
)
)
S(x) = Im(E(x)) = \dfrac{1}{2}(E(x)-E(-x))
S(x)=Im(E(x))=21(E(x)−E(−x))
CKKS 自举的流程为:

Homomorphic Matrix Multiplication
我们需要在 coefficient packing 和 slot packing 之间做变换:
- Coeff To Slot,就是对 slots 做 InvDFT 变换
- Slot To Coeff,就是对 slots 做 DFT 变换
对应的图形为:
IDFT
(
m
)
m
∈
R
N
DFT
(
m
)
∈
C
N
/
2
DFT
2
(
m
)
coeff to slot (IDFT)
∗
∗
原始密文
coeff
slot
slot to coeff (DFT)
∗
∗
\begin{array}{c} & \text{IDFT}(m) & m \in \mathbb R^N & \text{DFT}(m) \in \mathbb C^{N/2} & \text{DFT}^2(m)\\ \text{coeff to slot (IDFT)} & * & *\\ \text{原始密文} && \text{coeff} & \text{slot}\\ \text{slot to coeff (DFT)} &&& * & * \end{array}
coeff to slot (IDFT)原始密文slot to coeff (DFT)IDFT(m)∗m∈RN∗coeffDFT(m)∈CN/2slot∗DFT2(m)∗
为了计算 slots 的(公开)线性变换,[CHKKS18] 采取了 [HS14] 的矩阵-向量乘积的斜对角线算法:

它的每个 c t j ct_j ctj 是独立的,可以完全并行。旋转+数乘的数量 O ( N ) O(N) O(N),旋转+数乘的深度 O ( 1 ) O(1) O(1),使用 [HS15] 的大步小步法(Baby-Step Giant-Step algorithm)可以获得更低的复杂度:只需要 O ( N ) O(\sqrt N) O(N) 次旋转,

相较而言,同态的 FFT/NTT 需要 O ( log N ) O(\log N) O(logN) 层蝴蝶,并且每层的位移 2 j 2^j 2j 需要使用 Benes 网络实现。问题是:上述矩阵乘算法中的 R o t ( c t , j ) Rot(ct,j) Rot(ct,j),它真就是 Galois 群所提供的基本旋转置换么?是否也需要 Benes 网络呢?哦!可以按照 ζ → ζ 3 \zeta \to \zeta^3 ζ→ζ3 导致的旋转顺序对矩阵的行列做重排,然后仅使用基本的旋转置换就够了。
由于 CKKS 加密的是实系数多项式,只有一半的槽可用,另外一半与之共轭。
-
对于 Coeff To Slot,我们把 N N N 个实系数,迁移到 2 2 2 个密文的 N / 2 N/2 N/2 个复数槽中。因此需要把 N / 2 × N N/2 \times N N/2×N 的 DFT 矩阵切分为两个 N / 2 × N / 2 N/2 \times N/2 N/2×N/2 子矩阵,
D F T = [ U 0 ∣ U 1 ] , I D F T = 1 N ⋅ D F T † DFT = [U_0|U_1],\,\, IDFT = \dfrac{1}{N} \cdot DFT^\dagger DFT=[U0∣U1],IDFT=N1⋅DFT†两个子矩阵分别为
U 0 = [ 1 ζ 0 ⋯ ζ 0 N / 2 − 1 1 ζ 1 ⋯ ζ 1 N / 2 − 1 ⋮ ⋱ 1 ζ N / 2 − 1 ⋯ ζ N / 2 − 1 N / 2 − 1 ] , U 1 = [ ζ 0 N / 2 ζ 0 N / 2 + 1 ⋯ ζ 0 N − 1 ζ 1 N / 2 ζ 1 N / 2 + 1 ⋯ ζ 1 N − 1 ⋮ ⋱ ζ N / 2 − 1 N / 2 ζ N / 2 − 1 N / 2 + 1 ⋯ ζ N / 2 − 1 N − 1 ] U_0 = \begin{bmatrix} 1 & \zeta_0 &\cdots & \zeta_0^{N/2-1}\\ 1 & \zeta_1 &\cdots & \zeta_1^{N/2-1}\\ \vdots && \ddots\\ 1 & \zeta_{N/2-1} &\cdots & \zeta_{N/2-1}^{N/2-1}\\ \end{bmatrix},\,\, U_1 =\begin{bmatrix} \zeta_0^{N/2} & \zeta_0^{N/2+1} &\cdots & \zeta_0^{N-1}\\ \zeta_1^{N/2} & \zeta_1^{N/2+1} &\cdots & \zeta_1^{N-1}\\ \vdots && \ddots\\ \zeta_{N/2-1}^{N/2} & \zeta_{N/2-1}^{N/2+1} &\cdots & \zeta_{N/2-1}^{N-1}\\ \end{bmatrix} U0= 11⋮1ζ0ζ1ζN/2−1⋯⋯⋱⋯ζ0N/2−1ζ1N/2−1ζN/2−1N/2−1 ,U1= ζ0N/2ζ1N/2⋮ζN/2−1N/2ζ0N/2+1ζ1N/2+1ζN/2−1N/2+1⋯⋯⋱⋯ζ0N−1ζ1N−1ζN/2−1N−1 设置 ζ j = ζ 2 j + 1 \zeta_j=\zeta^{2j+1} ζj=ζ2j+1,其中的 ζ = exp ( π i / N ) \zeta=\exp(\pi i/N) ζ=exp(πi/N) 是 N N N 次本原根
槽的原始内容为 z ∈ C N / 2 z \in \mathbb C^{N/2} z∈CN/2,计算 z 0 = 1 N ( U 0 † ⋅ z + U 0 T ⋅ z ˉ ) z_0=\dfrac{1}{N}(U_0^\dagger \cdot z+U_0^T \cdot \bar z) z0=N1(U0†⋅z+U0T⋅zˉ) 和 z 1 = 1 N ( U 1 † ⋅ z + U 1 T ⋅ z ˉ ) z_1=\dfrac{1}{N}(U_1^\dagger \cdot z+U_1^T \cdot \bar z) z1=N1(U1†⋅z+U1T⋅zˉ),满足 [ z 0 ∣ z 1 ] = I n v D F T ( z ) [z_0|z_1]=InvDFT(z) [z0∣z1]=InvDFT(z)
-
对于 Slot To Coeff,我们把 2 2 2 个密文的 N / 2 N/2 N/2 个复数槽中存放的 N N N 个实数,迁移回单个密文的 N N N 个多项式系数上。这就是 Coeff To Slot 的逆过程,分别计算出 z 0 ′ = U 0 ⋅ z 0 z_0'=U_0 \cdot z_0 z0′=U0⋅z0 和 z 1 ′ = U 1 ⋅ z 1 z_1'=U_1 \cdot z_1 z1′=U1⋅z1,最后得到 z = z 0 ′ + z 1 ′ = D F T ( [ z 0 ∣ z 1 ] ) z=z_0'+z_1'= DFT([z_0|z_1]) z=z0′+z1′=DFT([z0∣z1])
Chimera
[CGGI20] 给出了实数环面(Torus)上的 T( R )LWE-based FHE 算法 TFHE,其密文的底层代数结构是连续的环面(而非 BGV/BFV、CKKS 的离散的环)。[BGGJ20] 提出了如何把 BFV、CKKS 的明密文空间都映射到环面上,可以将 BFV、CKKS、TFHE 的明密文空间统一起来,实现了三者之间的密文转换。
统一的明文空间是 T R \mathbb T_R TR,统一的密文空间是 T R 2 \mathbb T_R^2 TR2,它们都是 R = Z [ x ] / ( x N + 1 ) R=\mathbb Z[x]/(x^N+1) R=Z[x]/(xN+1) 模。
- BFV 方案:明文空间 R P ≅ P − 1 R / R ⊆ T R R_P \cong P^{-1}R/R \subseteq \mathbb T_R RP≅P−1R/R⊆TR,密文空间 R q ≅ q − 1 R / R ⊆ T R R_q \cong q^{-1}R/R \subseteq \mathbb T_R Rq≅q−1R/R⊆TR
- CKKS 方案:明文空间 { f ∈ R q : ∥ f ∥ ∞ ≤ 2 ρ } ≅ { f ∈ q − 1 R / R : ∥ f ∥ ∞ ≤ 2 ρ / q } ⊆ T R \{f \in R_q:\|f\|_\infty \le 2^\rho\} \cong \{f \in q^{-1}R/R:\|f\|_\infty \le 2^\rho/q\} \subseteq \mathbb T_R {f∈Rq:∥f∥∞≤2ρ}≅{f∈q−1R/R:∥f∥∞≤2ρ/q}⊆TR,密文空间 R q ≅ q − 1 R / R ⊆ T R R_q \cong q^{-1}R/R \subseteq \mathbb T_R Rq≅q−1R/R⊆TR
- TRLWE 方案:明文空间 T R \mathbb T_R TR,密文空间 T R \mathbb T_R TR
另外,TRGSW 方案:明文空间 R R R,密文空间 T R 2 \mathbb T_R^2 TR2,它加密的是环(其他三个方案都是加密的模)
FHE module structure & External product
[BGGJ20] 提出了全同态模结构,无噪声版本的定义如下:

可以验证,[CGGI20] 的两个方案 TRGSW 和 TRLWE 携带上 “外积”,它们组成了一个全同态模结构。点击这里,查看具体的构造。
我们现在列出 TFHE(TRLWE)的基本运算,
-
KeyGen:采样秘钥 s ← B ⊆ R s \gets \mathcal B \subseteq R s←B⊆R,诱导了相位 ϕ s : ( a , b ) ↦ b − s ⋅ a \phi_s:(a,b) \mapsto b-s \cdot a ϕs:(a,b)↦b−s⋅a,这里环 R R R 左作用于环面 T R \mathbb T_R TR
-
Encrypt:消息 μ ∈ T R \mu \in \mathbb T_R μ∈TR,密文 c = ( a , s ⋅ a + μ + e ) ∈ T R 2 c=(a,s \cdot a+\mu+e) \in \mathbb T_R^2 c=(a,s⋅a+μ+e)∈TR2
-
DecryptApprox:带噪的消息 ϕ s ( c ) ∈ T R \phi_s(c)\in \mathbb T_R ϕs(c)∈TR
-
DecryptRounded:预设离散子集 M ⊆ T R ≅ T N M \subseteq \mathbb T_R \cong \mathbb T^N M⊆TR≅TN,把 ϕ s ( c ) \phi_s(c) ϕs(c) 园整到最近的点
-
Public Linear Combinatrion:常数 a i ∈ R a_i \in R ai∈R,密文 c i = T R L W E S ( μ i ) c_i=TRLWE_S(\mu_i) ci=TRLWES(μi),输出(环的左作用)
T R L W E S ( ∑ i a i ⋅ μ i ) = ∑ i a i ⋅ c i ∈ T R 2 TRLWE_S(\sum_i a_i \cdot \mu_i)=\sum_i a_i \cdot c_i\in \mathbb T_R^2 TRLWES(i∑ai⋅μi)=i∑ai⋅ci∈TR2 -
Sample Extract:索引 i i i,加密了 μ ∈ T R \mu \in \mathbb T_R μ∈TR 的 TRLWE 密文 T R L W E S ( μ ) = ( a , b ) TRLWE_S(\mu) = (a,b) TRLWES(μ)=(a,b),输出加密了系数 μ i ∈ T \mu_i \in \mathbb T μi∈T 的同一秘钥下的 TLWE 密文
T L W E S ( μ i ) = ( ( a i , a i − 1 , ⋯ , a i − N + 1 ) , b i ) TLWE_S(\mu_i) = ((a_i,a_{i-1},\cdots,a_{i-N+1}), b_i) TLWES(μi)=((ai,ai−1,⋯,ai−N+1),bi)(原始论文中如此,但是不是少了负号啊?反循环的系数卷积。或者是,每个 i i i 对应的 S S S 分别是把原始 S S S 的对应若干位取了负号)
-
External Product:加密了 μ r ∈ R \mu_r \in R μr∈R 的 TRGSW 密文 c r c_r cr,加密了 μ m ∈ T R \mu_m \in \mathbb T_R μm∈TR 的 TRLWE 密文 c m c_m cm,输出加密了 μ r ⋅ μ m ∈ T R \mu_r \cdot \mu_m \in \mathbb T_R μr⋅μm∈TR 的 TRLWE 密文
c r ⊡ α c m : = c r ⋅ G α − 1 ( c m ) c_r \boxdot_\alpha c_m := c_r \cdot G^{-1}_\alpha(c_m) cr⊡αcm:=cr⋅Gα−1(cm)其中 α \alpha α 是动态的精度(当前噪声的标准差)。给定一个足够精度 2 − l 2^{-l} 2−l 的 TRGSW 密文 A A A,所编码的 μ A ⋅ G l \mu_A \cdot G_l μA⋅Gl 前面的 l ′ = − log α ≤ l l'=-\log\alpha \le l l′=−logα≤l 个小方阵,就足够计算外积了。
噪声规模是
V a r ( E r r ( c r ⊡ α c m ) ) ≤ 2 l N ⋅ V a r ( E r r ( c r ) ) + 1 + N 4 ∥ r ∥ 2 2 α 2 + ∥ r ∥ 2 2 ⋅ V a r ( E r r ( c m ) ) Var(Err(c_r \boxdot_\alpha c_m)) \le 2lN \cdot Var(Err(c_r)) + \dfrac{1+N}{4}\|r\|_2^2\alpha^2 + \|r\|_2^2 \cdot Var(Err(c_m)) Var(Err(cr⊡αcm))≤2lN⋅Var(Err(cr))+41+N∥r∥22α2+∥r∥22⋅Var(Err(cm))选取精度 α \alpha α,设置密文噪声的方差为 V a r ( E r r ( c r ) ) = α 2 Var(Err(c_r))=\alpha^2 Var(Err(cr))=α2,使得噪声主项是 ∥ r ∥ 2 2 ⋅ V a r ( E r r ( c m ) ) \|r\|_2^2 \cdot Var(Err(c_m)) ∥r∥22⋅Var(Err(cm))
-
Functional Key-Switch:任意的 κ \kappa κ-Lipschitz 线性态射 f : T k → T R f:\mathbb T^k \to \mathbb T_R f:Tk→TR,给定 k k k 个 TLWE 密文(不需要 n = N n=N n=N)
c i = T L W E S ( μ i ) ∈ T n + 1 c_i=TLWE_{S}(\mu_i) \in \mathbb T^{n+1} ci=TLWES(μi)∈Tn+1
给定秘钥切换秘钥(TRLWE 格式,密文的二进制分解 + 秘钥的 R R R 模线性组合)
K S i j = T R L W E K , α ( S i / 2 j ) KS_{ij}=TRLWE_{K,\alpha}(S_i/2^j) KSij=TRLWEK,α(Si/2j)存在某算法(详见 TFHE 的秘钥切换算法),输出
c = T R L W E K ( f ( μ 1 , ⋯ , μ k ) ) ∈ T R 2 c=TRLWE_K(f(\mu_1,\cdots,\mu_k)) \in \mathbb T_R^2 c=TRLWEK(f(μ1,⋯,μk))∈TR2噪声规模是
V a r ( E r r ( c ) ) ≤ κ 2 max i ( V a r ( E r r ( c i ) ) ) + α 2 ( l N 2 + N 4 ) Var(Err(c)) \le \kappa^2 \max_i(Var(Err(c_i))) + \alpha^2(lN^2+\dfrac{N}{4}) Var(Err(c))≤κ2imax(Var(Err(ci)))+α2(lN2+4N)选取精度 α \alpha α,使得噪声主项是 κ 2 max i ( V a r ( E r r ( c i ) ) ) \kappa^2 \max_i(Var(Err(c_i))) κ2maxi(Var(Err(ci)))

-
Functional Gate Bootstrap:任意的反循环非线性态射 f : ( 2 N ) − 1 Z / Z ⊆ T → T f:(2N)^{-1}\mathbb Z/\mathbb Z \subseteq \mathbb T \to \mathbb T f:(2N)−1Z/Z⊆T→T,满足 f ( x + 1 / 2 ) = − f ( x ) f(x+1/2)=-f(x) f(x+1/2)=−f(x),给定某个 TLWE 密文(不需要 n = N n=N n=N)
c = T L W E K ( μ ) ∈ ( ( 2 N ) − 1 Z / Z ) n + 1 ⊆ T n + 1 c=TLWE_K(\mu) \in ((2N)^{-1}\mathbb Z/\mathbb Z)^{n+1} \subseteq \mathbb T^{n+1} c=TLWEK(μ)∈((2N)−1Z/Z)n+1⊆Tn+1给定自举秘钥(TRGSW 格式,外积 + 基于 MUX 的盲旋转)
B K i = T R G S W S , α ( K i ) BK_i=TRGSW_{S,\alpha}(K_i) BKi=TRGSWS,α(Ki)存在某算法(详见 TFHE 的盲旋转/门自举算法),输出
c ′ = T L W E S ( f ( ϕ K ( c ) ) ) ∈ T N + 1 c'=TLWE_S(f(\phi_K(c))) \in \mathbb T^{N+1} c′=TLWES(f(ϕK(c)))∈TN+1噪声规模是
V a r ( E r r ( c ′ ) ) ≤ α 2 n ( 2 l N + N + 5 4 + l ) Var(Err(c')) \le \alpha^2n(2lN+N+\dfrac{5}{4}+l) Var(Err(c′))≤α2n(2lN+N+45+l)选取精度 α \alpha α,使得自举后 c ′ c' c′ 的噪声规模比原始 c c c 的噪声规模小得多

在三种方案的密文之间转换时,需要频繁用到 TRLWE 的上述操作:线性组合(同态解密)、系数提取(获取 TLWE 密文)、外积(构造内积)、线性态射的秘钥切换(在 coeff 和 slot 之间切换)、自举。
TRLWE as Bridge
在 Chimera 中,使用 TRLWE 作为桥梁:

对于 BFV(红箭头),
- 采取 slot packing 编码方式的消息 p μ i ∈ Z p p\mu_i \in \mathbb Z_p pμi∈Zp 的单个 BFV 密文,转换为 coeff packing 编码方式的消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的单个 TRLWE 密文,最后可以提取出 N N N 个消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的 TLWE 密文
- 至多 N N N 个消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的 TLWE 密文,组合成 slot packing 编码方式的消息 p μ i ∈ Z p p\mu_i \in \mathbb Z_p pμi∈Zp 的单个 BFV 密文
对于 CKKS(绿箭头),
- 采取 coeff packing 编码方式的消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的单个 CKKS 密文(也可以利用 Slot to Coeff 程序获取 slot packing 的消息,但是需要 D F T ( μ ⃗ ) DFT(\vec \mu) DFT(μ) 是实的),可以立即地转换为 coeff packing 编码方式的消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的单个 TRLWE 密文,最后可以提取出 N N N 个消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的 TLWE 密文
- 至多 N / 2 N/2 N/2 个消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的 TLWE 密文,采用 CKKS 自举技巧的变体,组合成 slot packing 编码方式的消息 exp ( 2 π i μ i ) ∈ C \exp(2\pi i\mu_i) \in \mathbb C exp(2πiμi)∈C 的单个 CKKS 密文,最后可以利用 sin \sin sin 函数以及 Slot to Coeff 程序得到 coeff packing 编码方式的消息 μ i ∈ T \mu_i \in \mathbb T μi∈T 的单个 CKKS 密文
对于 BFV-BigNum(蓝箭头),明文模数选取为
P
=
x
−
p
P=x-p
P=x−p,此时
R
P
≅
Z
p
N
+
1
R_P \cong \mathbb Z_{p^N+1}
RP≅ZpN+1,并且
P
−
1
=
−
1
p
N
+
1
∑
i
=
0
N
−
1
p
N
−
i
−
1
x
i
P^{-1} = \dfrac{-1}{p^N+1} \sum_{i=0}^{N-1} p^{N-i-1}x^i
P−1=pN+1−1i=0∑N−1pN−i−1xi
于是同构映射 R P ≅ P − 1 R / R → Z p N + 1 R_P \cong P^{-1}R/R \to \mathbb Z_{p^N+1} RP≅P−1R/R→ZpN+1 恰好就是提取前导项 x N − 1 x^{N-1} xN−1 的系数。在密文转换时,直接与 TLWE 做转换。
Application
在 TFHE 密文下计算:
- 稀疏的、深度大的布尔运算
- 线性运算(秘钥切换)
- 反循环的非线性运算(盲旋转/自举)
- 延迟较低的自举
在 BFV 密文下计算:
- 密集的、深度浅的整数运算(SIMD)
- 稀疏表示的非线性多项式(拉格朗日插值)
- 均摊成本低的自举
在 CKKS 密文下计算:
- 密集的、深度浅的浮点数运算(SIMD)
- 明文槽的线性变换(同态的矩阵乘)
- 非线性函数(傅里叶级数/泰勒级数)
BFV
BFV over Torus
原始 BFV 的明文空间是
R
P
≅
P
−
1
R
/
R
⊆
T
R
R_P \cong P^{-1}R/R \subseteq \mathbb T_R
RP≅P−1R/R⊆TR,其中
P
∈
Z
[
x
]
P \in \mathbb Z[x]
P∈Z[x] 在
Q
[
x
]
\mathbb Q[x]
Q[x] 中可逆。同构映射为
u
∈
T
R
↦
P
⋅
u
∈
R
P
u \in \mathbb T_R \mapsto P\cdot u \in R_P
u∈TR↦P⋅u∈RP
我们称 R P R_P RP 是环面 T R \mathbb T_R TR 的 P P P-扭曲(torsion)
我们现在为 native 明文空间
M
:
=
P
−
1
R
/
R
M:=P^{-1}R/R
M:=P−1R/R 装备上乘法。定义离散环面
M
⊆
T
R
M \subseteq \mathbb T_R
M⊆TR 的蒙哥马利内积(internal Mongomery-type product)
μ
1
⊡
P
μ
2
↦
P
⋅
μ
1
⋅
μ
2
(
m
o
d
Z
)
\mu_1 \boxdot_P \mu_2 \mapsto P \cdot \mu_1 \cdot \mu_2 \pmod{\mathbb Z}
μ1⊡Pμ2↦P⋅μ1⋅μ2(modZ)
其中的 ⋅ \cdot ⋅ 算符,是从 Z [ x ] , M \mathbb Z[x],M Z[x],M 提升到 Q [ x ] \mathbb Q[x] Q[x] 上运算的。
环面上的 BFV 方案:
-
KeyGen:
- 均匀采样 s ← B s \gets \mathcal B s←B,它是短的整系数多项式
-
Enc:
- 明文 μ ∈ M ⊆ T R \mu \in M \subseteq \mathbb T_R μ∈M⊆TR
- 均匀采样 a ← T R a \gets \mathbb T_R a←TR,零中心高斯采样 e ← T R e \gets \mathbb T_R e←TR
- 计算 b : = s ⋅ a + e ∈ T R b := s\cdot a+e \in \mathbb T_R b:=s⋅a+e∈TR,满足 ϕ s ( a , b ) = e ≈ 0 \phi_s(a,b)=e \approx 0 ϕs(a,b)=e≈0
- 密文 c : = ( a , b ) + ( 0 , μ ) c:=(a,b)+(0,\mu) c:=(a,b)+(0,μ),是长度 2 2 2 的列向量
-
Dec:
- 密文 ( a , b ′ ) ∈ T R × T R (a,b') \in \mathbb T_R \times \mathbb T_R (a,b′)∈TR×TR
- 计算 ϕ s ( a , b ′ ) = e + μ ∈ T R \phi_s(a,b') = e+\mu \in \mathbb T_R ϕs(a,b′)=e+μ∈TR
- 圆整到 μ ∈ M \mu \in M μ∈M
-
Add(同态的 M M M 上的加法):
- 密文 c 1 = B F V s ( μ 1 ) , c 2 = B F V s ( μ 2 ) c_1 = BFV_s(\mu_1), c_2 = BFV_s(\mu_2) c1=BFVs(μ1),c2=BFVs(μ2),属于 R R R 模 T R 2 \mathbb T_R^2 TR2
- 计算 R R R 模的加法 c 3 = c 1 + c 2 = B F V s ( μ 1 + μ 2 ) c_3 = c_1+c_2 = BFV_s(\mu_1+\mu_2) c3=c1+c2=BFVs(μ1+μ2)
-
Internal product(同态的 M M M 上的内积):
-
给定重线性化秘钥 R K = T R G S W s , α ( s ) RK=TRGSW_{s,\alpha}(s) RK=TRGSWs,α(s)(原始 BFV 采取 R K j = T R L W E s ( s 2 / 2 j ) RK_j=TRLWE_s(s^2/2^j) RKj=TRLWEs(s2/2j))
-
密文 c i = B F V s ( μ i ) c_i = BFV_s(\mu_i) ci=BFVs(μi) 提升到 ( a i , b i ) ∈ R R (a_i,b_i) \in R_\mathbb R (ai,bi)∈RR,系数范围 [ − 1 / 2 , 1 / 2 ) [-1/2,1/2) [−1/2,1/2),使得在 R R R_\mathbb R RR 上可以计算乘法
-
计算 c i ( s ) c_i(s) ci(s) 的 Montgomery 版本多项式乘积(提升到 R R R_\mathbb R RR 上的乘法,虽然 ⊡ P , α \boxdot_{P,\alpha} ⊡P,α 仅仅对于子集 M ⊆ T R M \subseteq \mathbb T_R M⊆TR 有定义), C 2 = P a 1 a 2 C_2=P a_1 a_2 C2=Pa1a2, C 1 = P ( a 1 b 2 + a 2 b 1 ) C_1=P (a_1b_2 + a_2b_1) C1=P(a1b2+a2b1), C 0 = P b 1 b 2 C_0=P b_1 b_2 C0=Pb1b2
-
消除密文多项式的二次项,由于
E n c M ( s 2 ⋅ C 2 ) = E n c R ( s 2 ) ⊡ α E n c M ( C 2 ) = E n c R ( s ) ⊡ α E n c M ( s ⋅ C 2 ) Enc_M(s^2 \cdot C_2) = Enc_R(s^2) \boxdot_\alpha Enc_M(C_2) = Enc_R(s) \boxdot_\alpha Enc_M(s \cdot C_2) EncM(s2⋅C2)=EncR(s2)⊡αEncM(C2)=EncR(s)⊡αEncM(s⋅C2)Chimera 采用 R K = E n c R ( s ) RK=Enc_R(s) RK=EncR(s),对应的密文 E n c M ( s ⋅ C 2 ) = ( − C 2 , 0 ) Enc_M(s \cdot C_2)=(-C_2,0) EncM(s⋅C2)=(−C2,0)
原始 BFV 采用了 R K = E n c R ( s 2 ) RK=Enc_R(s^2) RK=EncR(s2),对应的密文 E n c M ( C 2 ) = ( 0 , C 2 ) Enc_M(C_2)=(0,C_2) EncM(C2)=(0,C2),但是元素 s 2 s^2 s2 的范数相对更大,导致外积的噪声更大
-
利用与 TRGSW 的外积,构造出 BFV 的密文内积(注意 TRLWE 的密文内积未定义,环面 T R \mathbb T_R TR 上并没有关于 P P P 的蒙哥马利内积)
c 1 ⊡ P , α c 2 : = ( C 1 , C 0 ) − R K ⊡ α ( C 2 , 0 ) c_1 \boxdot_{P,\alpha} c_2 := (C_1,C_0) - RK \boxdot_\alpha (C_2,0) c1⊡P,αc2:=(C1,C0)−RK⊡α(C2,0)容易验证, c 1 ⊡ P , α c 2 = B F V s ( μ 1 ⊡ P μ 2 ) c_1 \boxdot_{P,\alpha} c_2 = BFV_s(\mu_1 \boxdot_P \mu_2) c1⊡P,αc2=BFVs(μ1⊡Pμ2)
噪声规模是
V a r ( E r r ( c 1 ⊡ P , α c 2 ) ) ≤ 1 + N + N 2 2 ∥ P ∥ 2 2 ⋅ max i V a r ( E r r ( c i ) ) + α 2 ( 2 l N + N + N 2 4 ) Var(Err(c_1 \boxdot_{P,\alpha} c_2)) \le \dfrac{1+N+N^2}{2}\|P\|_2^2 \cdot \max_i Var(Err(c_i)) + \alpha^2(2lN+\dfrac{N+N^2}{4}) Var(Err(c1⊡P,αc2))≤21+N+N2∥P∥22⋅imaxVar(Err(ci))+α2(2lN+4N+N2)选取合适的 α \alpha α,使得主项是 1 + N + N 2 2 ∥ P ∥ 2 2 ⋅ max i V a r ( E r r ( c i ) ) \dfrac{1+N+N^2}{2}\|P\|_2^2 \cdot \max_i Var(Err(c_i)) 21+N+N2∥P∥22⋅maxiVar(Err(ci))
-
-
Modulus switch:BFV 不需要模切换,原始方案的思路就是用 Z q \mathbb Z_q Zq 模拟 q − 1 Z / Z q^{-1}\mathbb Z/\mathbb Z q−1Z/Z,噪声被自然地控制了(小数相乘会变得更小)
现在 BFV 的明文是 μ ∈ M ⊆ T R \mu \in M \subseteq \mathbb T_R μ∈M⊆TR,密文是 c = ( a , b ) ∈ T R 2 c=(a,b) \in \mathbb T_R^2 c=(a,b)∈TR2,它们与 TRLWE 的明密文空间相兼容。
BFV to TFHE
选取明文模数 P = p ∈ Z P=p \in \mathbb Z P=p∈Z 是素数,满足 2 N ∣ p − 1 2N|p-1 2N∣p−1 使得 Z p \mathbb Z_p Zp 中存在 2 N 2N 2N 次本原单位根。
Coeff packing:明文空间 M = p − 1 R / R M = p^{-1}R/R M=p−1R/R,我们以标准基 { 1 , x , ⋯ , x N − 1 } \{1,x,\cdots,x^{N-1}\} {1,x,⋯,xN−1} 将它转换为 M ≅ p − 1 Z N / Z N M \cong p^{-1}\mathbb Z^N/\mathbb Z^N M≅p−1ZN/ZN,因此 M M M 可以视为矩阵 p − 1 I N p^{-1}I_N p−1IN 生成的正交格,packing raduius 是 1 / 2 P 1/2P 1/2P
Slot packing:明文空间
M
≅
R
p
≅
Z
p
N
M \cong R_p \cong \mathbb Z_p^N
M≅Rp≅ZpN,令
ζ
0
,
⋯
,
ζ
N
−
1
∈
Z
p
\zeta_0,\cdots,\zeta_{N-1} \in \mathbb Z_p
ζ0,⋯,ζN−1∈Zp 是
x
n
+
1
x^n+1
xn+1 的所有根,同构映射为
N
T
T
:
μ
∈
p
−
1
R
/
R
↦
z
=
[
(
p
μ
)
(
ζ
0
)
,
⋯
,
(
p
μ
)
(
ζ
N
−
1
)
]
∈
Z
p
N
NTT:\mu \in p^{-1}R/R \mapsto z=[(p\mu)(\zeta_0),\cdots,(p\mu)(\zeta_{N-1})] \in \mathbb Z_p^N
NTT:μ∈p−1R/R↦z=[(pμ)(ζ0),⋯,(pμ)(ζN−1)]∈ZpN
从
p
μ
→
z
p\mu \to z
pμ→z 的线性变换为:
V
D
M
=
[
1
ζ
0
⋯
ζ
0
N
−
1
1
ζ
1
⋯
ζ
1
N
−
1
⋮
⋱
1
ζ
N
−
1
⋯
ζ
N
−
1
N
−
1
]
(
m
o
d
p
)
VDM=\begin{bmatrix} 1 & \zeta_0 & \cdots & \zeta_0^{N-1}\\ 1 & \zeta_1 & \cdots & \zeta_1^{N-1}\\ \vdots && \ddots\\ 1 & \zeta_{N-1} & \cdots & \zeta_{N-1}^{N-1}\\ \end{bmatrix} \pmod{p}
VDM=
11⋮1ζ0ζ1ζN−1⋯⋯⋱⋯ζ0N−1ζ1N−1ζN−1N−1
(modp)
给定 BFV 密文
c
=
(
a
,
b
+
μ
)
∈
T
R
2
c=(a,b+\mu) \in \mathbb T_R^2
c=(a,b+μ)∈TR2,为了方便矩阵运算,我们把
a
a
a 写成反循环的行向量,
s
s
s 和
b
b
b 写成列向量(
Z
\mathbb Z
Z 是交换环,右模 = 左模),于是把
c
c
c 写成矩阵形式
C
∈
T
N
×
(
N
+
1
)
C \in \mathbb T^{N \times (N+1)}
C∈TN×(N+1)(也就是
N
N
N 个 TLWE 密文),
D
e
c
s
(
c
)
=
[
a
N
−
1
a
N
−
2
⋯
a
1
a
0
b
N
−
1
+
μ
N
−
1
a
N
−
2
a
N
−
3
⋯
a
0
−
a
N
−
1
b
N
−
2
+
μ
N
−
2
⋱
⋮
a
0
−
a
N
−
1
⋯
−
a
2
−
a
1
b
0
+
μ
0
]
⋅
[
−
s
0
−
s
1
⋮
−
s
N
−
1
1
]
≈
[
μ
N
−
1
μ
N
−
2
⋮
μ
0
]
∈
(
p
−
1
Z
/
Z
)
N
Dec_s(c) = \left[\begin{array}{ccccc|c} a_{N-1} & a_{N-2} & \cdots & a_1 & a_0 & b_{N-1}+\mu_{N-1}\\ a_{N-2} & a_{N-3} & \cdots & a_0 & -a_{N-1} & b_{N-2}+\mu_{N-2}\\ &&\ddots&&&\vdots\\ a_{0} & -a_{N-1} & \cdots & -a_{2} & -a_{1} & b_0+\mu_{0}\\ \end{array}\right] \cdot \begin{bmatrix} -s_0\\-s_1\\\vdots\\-s_{N-1}\\1 \end{bmatrix} \approx \begin{bmatrix} \mu_{N-1}\\\mu_{N-2}\\\vdots\\\mu_{0} \end{bmatrix} \in (p^{-1} \mathbb Z/\mathbb Z)^N
Decs(c)=
aN−1aN−2a0aN−2aN−3−aN−1⋯⋯⋱⋯a1a0−a2a0−aN−1−a1bN−1+μN−1bN−2+μN−2⋮b0+μ0
⋅
−s0−s1⋮−sN−11
≈
μN−1μN−2⋮μ0
∈(p−1Z/Z)N
给定矩阵
F
∈
Z
N
×
N
F \in \mathbb Z^{N \times N}
F∈ZN×N(环面
T
\mathbb T
T 是
Z
\mathbb Z
Z 模),可以对多项式的系数
μ
i
\mu_i
μi 做线性变换(通过对
C
C
C 的每一列
X
i
a
(
x
)
(
m
o
d
x
N
+
1
)
X^ia(x) \pmod{x^N+1}
Xia(x)(modxN+1) 做
F
F
F 变换),
(
F
⋅
C
)
⋅
(
−
s
,
1
)
=
F
⋅
[
μ
N
−
1
μ
N
−
2
⋮
μ
0
]
+
F
⋅
e
(F \cdot C) \cdot (-s,1) = F \cdot \begin{bmatrix} \mu_{N-1}\\\mu_{N-2}\\\vdots\\\mu_{0} \end{bmatrix} +F \cdot e
(F⋅C)⋅(−s,1)=F⋅
μN−1μN−2⋮μ0
+F⋅e
为了减少噪声 F ⋅ e F \cdot e F⋅e 的规模,我们可以把 F F F 约束为系数范围是 [ − p / 2 , p / 2 ) [-p/2,p/2) [−p/2,p/2) 的整数矩阵(离散环面 p − 1 Z / Z ⊆ T p^{-1} \mathbb Z/\mathbb Z \subseteq \mathbb T p−1Z/Z⊆T 不仅是 Z \mathbb Z Z 模,也是 Z p \mathbb Z_p Zp 模)
对于 slot 内的消息
z
=
N
T
T
(
p
μ
)
∈
Z
p
N
z=NTT(p\mu) \in \mathbb Z_p^N
z=NTT(pμ)∈ZpN,其上的线性变换为
F
⋅
(
V
D
M
⋅
(
p
⋅
μ
)
)
F \cdot (VDM \cdot (p \cdot \mu))
F⋅(VDM⋅(p⋅μ))
由于 μ ∈ ( p − 1 Z / Z ) N \mu \in (p^{-1}\mathbb Z/\mathbb Z)^N μ∈(p−1Z/Z)N,因此 p ⋅ μ ∈ Z p N p \cdot \mu \in \mathbb Z_p^N p⋅μ∈ZpN,从而可以在 Z p \mathbb Z_p Zp 上计算 NTT 变换。
但是密文
C
∈
T
N
×
(
N
+
1
)
C \in \mathbb T^{N \times (N+1)}
C∈TN×(N+1) 并不是
Z
p
\mathbb Z_p
Zp 模,我们需要把
V
D
M
∈
Z
p
N
×
N
VDM \in \mathbb Z_p^{N \times N}
VDM∈ZpN×N 提升到
Z
N
×
N
\mathbb Z^{N \times N}
ZN×N 上才存在环作用。我们计算:
(
F
⋅
V
D
M
)
⋅
C
⋅
(
−
s
,
1
)
≈
p
−
1
(
F
⋅
z
)
∈
(
p
−
1
Z
/
Z
)
N
(F \cdot VDM) \cdot C \cdot (-s,1) \approx p^{-1}(F \cdot z) \in (p^{-1}\mathbb Z/\mathbb Z)^N
(F⋅VDM)⋅C⋅(−s,1)≈p−1(F⋅z)∈(p−1Z/Z)N
同理,我们应当把
F
⋅
V
D
M
F \cdot VDM
F⋅VDM 表示为系数范围是
[
−
p
/
2
,
p
/
2
)
[-p/2,p/2)
[−p/2,p/2) 的整数矩阵,以减少噪声规模。
使用线性态射是 F ⋅ V D M F \cdot VDM F⋅VDM 的秘钥切换过程(单个 TRLWE 密文被视为 N N N 个 TLWE 密文),就实现了 BFV 到 TFHE 的密文转换:
- 输入单个 slot packing 编码的消息 z ∈ Z p N z \in \mathbb Z_p^N z∈ZpN 的 BFV over Torus 密文,以及 Z p \mathbb Z_p Zp 上的线性函数 f f f
- 输出单个 coeff packing 编码的消息 p − 1 f ( z ) p^{-1}f(z) p−1f(z) 的 TRLWE 密文
- 可以通过 Sample Extract 提取出 N N N 个系数的 TLWE 密文

由于
F
⋅
V
D
M
(
m
o
d
p
)
F \cdot VDM \pmod p
F⋅VDM(modp) 是一个
(
N
p
/
2
)
(Np/2)
(Np/2)-Lipschitz 态射,输出的噪声规模为
V
a
r
(
E
r
r
(
c
′
)
)
≤
(
N
p
2
)
2
⋅
V
a
r
(
E
r
r
(
c
)
)
+
α
2
⋅
(
l
N
2
+
N
4
)
Var(Err(c')) \le (\dfrac{Np}{2})^2 \cdot Var(Err(c)) + \alpha^2 \cdot (lN^2+\dfrac{N}{4})
Var(Err(c′))≤(2Np)2⋅Var(Err(c))+α2⋅(lN2+4N)
选取合适的精度 α \alpha α,使得 ( N p / 2 ) 2 ⋅ V a r ( E r r ( c ) ) (Np/2)^2 \cdot Var(Err(c)) (Np/2)2⋅Var(Err(c)) 成为主项。
TFHE to BFV
现在我们把 TLWE 密文转换为 BFV 密文。由于 TLWE 加密的消息是 T \mathbb T T,而 BFV 加密的消息是 Z p \mathbb Z_p Zp,因此对于态射 g : T → Z p g:\mathbb T \to \mathbb Z_p g:T→Zp,任意的 x = p ⋅ y ∈ T x=p\cdot y \in\mathbb T x=p⋅y∈T 总使得 g ( x ) = p ⋅ g ( y ) = 0 ∈ Z p g(x)=p \cdot g(y)=0 \in \mathbb Z_p g(x)=p⋅g(y)=0∈Zp,所以必须限制 g g g 的值域是离散的。
我们设置 g : Z p k → Z p N g:\mathbb Z_p^k \to \mathbb Z_p^N g:Zpk→ZpN 是线性态射,对应的矩阵 G ∈ Z N × k G \in \mathbb Z^{N \times k} G∈ZN×k。在密文转换之前,必须先利用 Gate Bootstrapping,
- 把 TLWE 密文的明文空间约束为 p − 1 Z / Z p^{-1}\mathbb Z/\mathbb Z p−1Z/Z(盲旋转 LUT 的取值设置为 p − 1 p^{-1} p−1 整数倍)
- 并且把噪声水平降低到 BFV 可容忍的范围(TFHE 能够容忍很高的噪声比率)
给定
k
≤
N
k \le N
k≤N 个 TLWE 密文,按照行向量排列为矩阵
C
=
[
a
0
,
0
a
0
,
1
⋯
a
0
,
n
−
1
b
0
+
μ
0
a
1
,
0
a
1
,
1
⋯
a
1
,
n
−
1
b
1
+
μ
1
⋱
⋮
a
k
−
1
,
0
a
k
−
1
,
1
⋯
a
k
−
1
,
n
−
1
b
k
−
1
+
μ
k
−
1
]
∈
T
k
×
(
n
+
1
)
C = \left[\begin{array}{cccc|c} a_{0,0} & a_{0,1} & \cdots & a_{0,n-1} & b_0+\mu_0\\ a_{1,0} & a_{1,1} & \cdots & a_{1,n-1} & b_1+\mu_1\\ &&\ddots&&\vdots\\ a_{k-1,0} & a_{k-1,1} & \cdots & a_{k-1,n-1} & b_{k-1}+\mu_{k-1}\\ \end{array}\right] \in \mathbb T^{k \times (n+1)}
C=
a0,0a1,0ak−1,0a0,1a1,1ak−1,1⋯⋯⋱⋯a0,n−1a1,n−1ak−1,n−1b0+μ0b1+μ1⋮bk−1+μk−1
∈Tk×(n+1)
我们首先将
V
D
M
−
1
⋅
G
VDM^{-1} \cdot G
VDM−1⋅G 提升为
Z
N
×
k
\mathbb Z^{N \times k}
ZN×k 内的矩阵(并约束系数范围),然后计算矩阵乘(分别乘以密文
C
C
C 的每一列)
(
V
D
M
−
1
⋅
G
⋅
C
)
⋅
(
−
s
,
1
)
≈
V
D
M
−
1
⋅
(
G
⋅
μ
)
=
p
−
1
⋅
I
N
T
T
(
g
(
p
μ
)
)
∈
(
p
−
1
Z
/
Z
)
N
(VDM^{-1} \cdot G \cdot C) \cdot (-s,1) \approx VDM^{-1} \cdot (G \cdot \mu) = p^{-1} \cdot INTT(g(p\mu)) \in (p^{-1}\mathbb Z/\mathbb Z)^N
(VDM−1⋅G⋅C)⋅(−s,1)≈VDM−1⋅(G⋅μ)=p−1⋅INTT(g(pμ))∈(p−1Z/Z)N
使用线性态射是 V D M − 1 ⋅ G VDM^{-1} \cdot G VDM−1⋅G 的秘钥切换过程,就实现了 TFHE 到 BFV 的密文转换:
- 输入 k k k 个消息 μ i ∈ p − 1 Z / Z \mu_i \in p^{-1}\mathbb Z/\mathbb Z μi∈p−1Z/Z 的 TLWE 密文,以及 Z p \mathbb Z_p Zp 上的线性函数 g g g
- 输出单个 slot packing 编码的消息 g ( p μ ) g(p\mu) g(pμ) 的 BFV over Torus 密文

输出的噪声规模为
V
a
r
(
E
r
r
(
c
′
)
)
≤
(
N
p
2
)
2
⋅
max
i
V
a
r
(
E
r
r
(
c
i
)
)
+
α
2
⋅
(
l
N
2
+
N
4
)
Var(Err(c')) \le (\dfrac{Np}{2})^2 \cdot \max_iVar(Err(c_i)) + \alpha^2 \cdot (lN^2+\dfrac{N}{4})
Var(Err(c′))≤(2Np)2⋅imaxVar(Err(ci))+α2⋅(lN2+4N)
选取合适的精度 α \alpha α,使得 ( N p 2 ) 2 ⋅ max i V a r ( E r r ( c i ) ) (\dfrac{Np}{2})^2 \cdot \max_i Var(Err(c_i)) (2Np)2⋅maxiVar(Err(ci)) 成为主项。额外要求输入密文的 max i V a r ( E r r ( c i ) ) \max_i Var(Err(c_i)) maxiVar(Err(ci)) 本身就很小(自举时设置足够大的精度),从而使得 BFV 可以容忍此噪声。
BFV-big-number
博主我还没看过这个方案,略。。。
CKKS
CKKS over Torus
原始 CKKS 的明文空间是:
{
f
∈
R
q
:
∥
f
∥
∞
≤
2
ρ
}
≅
{
f
∈
q
−
1
R
/
R
:
∥
f
∥
∞
≤
2
ρ
/
q
}
⊆
T
R
\{f \in R_q:\|f\|_\infty \le 2^\rho\} \cong \{f \in q^{-1}R/R:\|f\|_\infty \le 2^\rho/q\} \subseteq \mathbb T_R
{f∈Rq:∥f∥∞≤2ρ}≅{f∈q−1R/R:∥f∥∞≤2ρ/q}⊆TR
按照 IEEE754 标准,浮点数表示为
(
σ
,
τ
,
m
)
(\sigma,\tau,m)
(σ,τ,m),其中
σ
∈
{
0
,
1
}
\sigma \in \{0,1\}
σ∈{0,1} 是符号,
τ
∈
Z
\tau \in \mathbb Z
τ∈Z 是指数,
0
≤
m
<
1
0 \le m <1
0≤m<1 是尾数,尾数的精度为
ρ
∈
N
\rho \in \mathbb N
ρ∈N(也就是说
m
∈
2
−
ρ
Z
m \in 2^{-\rho}\mathbb Z
m∈2−ρZ),对应的浮点数是
(
−
1
)
σ
×
(
1.
m
)
×
2
τ
(-1)^\sigma \times (1.m) \times 2^\tau
(−1)σ×(1.m)×2τ
现在我们把明文(有限精度的复数)存放在 slots 上:
- 层数 L ∈ N L \in \mathbb N L∈N:代表同态计算能力,native 明文(环面元素)的规模 ∥ μ ∥ ∞ ≤ 2 − L \|\mu\|_\infty \le 2^{-L} ∥μ∥∞≤2−L
- 明文指数 τ ∈ Z \tau \in \mathbb Z τ∈Z:槽(浮点数)的指数
- 明文精度 ρ ∈ N \rho \in \mathbb N ρ∈N:槽(浮点数)的尾数精度
- 密文精度 α = 2 − ( L + ρ ) \alpha = 2^{-(L+\rho)} α=2−(L+ρ):大约是噪声的标准差
设置 CKKS 的 native 明文空间,
M
=
{
μ
∈
T
R
:
∥
μ
∥
∞
≤
2
−
L
}
M=\{\mu \in \mathbb T_R:\|\mu\|_\infty \le 2^{-L}\}
M={μ∈TR:∥μ∥∞≤2−L}
它的 SIMD 槽里的复数形如 z = m ⋅ 2 τ z=m \cdot 2^\tau z=m⋅2τ,其中 − 1 < m < 1 -1 <m<1 −1<m<1 是有限精度的尾数,满足 m ∈ 2 − ρ ( Z + i Z ) m \in 2^{-\rho}(\mathbb Z+i\mathbb Z) m∈2−ρ(Z+iZ)(包含了符号位)
令
ζ
∈
C
\zeta \in \mathbb C
ζ∈C 是
x
n
+
1
x^n+1
xn+1 的复数根(单位圆上的范数是
1
1
1),将精度
ρ
\rho
ρ 的元素
μ
∈
T
R
\mu \in \mathbb T_R
μ∈TR 提升到
R
[
x
]
\mathbb R[x]
R[x] 上,计算 DFT 得到槽的内容,
(
2
L
⋅
μ
)
(
ζ
i
)
=
m
i
∈
C
(2^L \cdot\mu)(\zeta_i) = m_i \in \mathbb C
(2L⋅μ)(ζi)=mi∈C
无限精度(足够大)的范数 1 1 1 的 DFT 行向量 [ 1 , ζ , ζ 2 , ⋯ , ζ N − 1 ] [1,\zeta,\zeta^2,\cdots,\zeta^{N-1}] [1,ζ,ζ2,⋯,ζN−1],和精度为 ρ \rho ρ、层数 L = 1 L=1 L=1 的范数上界 1 / 2 1/2 1/2 的 μ \mu μ 内积,获得的复数 m i m_i mi 精度为 ρ \rho ρ、范数约为 N / 2 \sqrt N/2 N/2。我们把浮点表示的复数 ( m i ∈ [ − 1 , 1 ] , τ ′ ) (m_i \in [-1,1],\tau') (mi∈[−1,1],τ′) 通过 IDFT 计算出 μ ∈ 2 − ρ R / R \mu \in 2^{-\rho}R/R μ∈2−ρR/R 以及恰当的指数 2 t 2^t 2t,使得 ∥ D F T ( 2 t μ ) − m ∥ ≤ 2 − ρ \|DFT(2^t \mu) - m\| \le 2^{-\rho} ∥DFT(2tμ)−m∥≤2−ρ 误差足够小,那么 τ = t + τ ′ \tau=t+\tau' τ=t+τ′ 就是它的指数,精度为 ρ \rho ρ
槽内的复数,存储格式如图:

环面上的 CKKS 方案:
-
KeyGen:
- 均匀采样 s ← B s \gets \mathcal B s←B,它是短的整系数多项式
-
Enc:
- 预设的精度 ρ \rho ρ 和层数 L L L,模数为 q = 2 L + ρ q=2^{L+\rho} q=2L+ρ,噪声规模 α = 1 / q \alpha=1/q α=1/q
- 给定明文 z = ( z 1 , ⋯ , z N / 2 ) ∈ C N / 2 z=(z_1,\cdots,z_{N/2}) \in \mathbb C^{N/2} z=(z1,⋯,zN/2)∈CN/2,它的存储格式任意
- 通过插值法找出整系数多项式 d ( x ) ∈ R d(x) \in R d(x)∈R,系数取值范围 [ − 2 ρ , 2 ρ ] [-2^\rho,2^\rho] [−2ρ,2ρ],以及对应的明文指数 τ ∈ Z \tau \in \mathbb Z τ∈Z,满足 ∥ D F T ( d ) ⋅ 2 τ − z ∥ ∞ ≤ 2 τ − ρ \|DFT(d) \cdot 2^\tau - z\|_\infty \le 2^{\tau-\rho} ∥DFT(d)⋅2τ−z∥∞≤2τ−ρ
- 设置 native 明文为 μ = d / q ∈ q − 1 R / R \mu=d/q \in q^{-1} R/R μ=d/q∈q−1R/R,满足 ∥ μ ∥ ∞ ≤ 2 − L \|\mu\|_\infty \le 2^{-L} ∥μ∥∞≤2−L(当 L = 1 L=1 L=1 时它恰好是 TRLWE 密文)
- 均匀采样 a ← T R a \gets \mathbb T_R a←TR,零中心高斯采样 e ← T R e \gets \mathbb T_R e←TR
- 计算 b : = s ⋅ a + e ∈ T R b := s\cdot a+e \in \mathbb T_R b:=s⋅a+e∈TR,满足 ϕ s ( a , b ) = e ≈ 0 \phi_s(a,b)=e \approx 0 ϕs(a,b)=e≈0
- 携带 tag 的 CKKS 密文 c : = ( ( a , b + μ ) , τ , L ) c:=((a,b+\mu),\tau,L) c:=((a,b+μ),τ,L)
-
Dec:
- 密文 ( ( a , b ′ ) , τ , L ) ∈ T R 2 × Z × N ((a,b'),\tau,L) \in \mathbb T_R^2 \times \mathbb Z \times \mathbb N ((a,b′),τ,L)∈TR2×Z×N
- 计算 ϕ s ( a , b ′ ) = e + μ ∈ T R \phi_s(a,b') = e+\mu \in \mathbb T_R ϕs(a,b′)=e+μ∈TR,
- 设置 q = 2 L + ρ q=2^{L+\rho} q=2L+ρ,圆整到 μ ∈ q − 1 R / R \mu \in q^{-1}R/R μ∈q−1R/R
- 明文 z = D F T ( q ⋅ μ ) ⋅ 2 τ ∈ C N / 2 z = DFT(q \cdot \mu) \cdot 2^\tau \in \mathbb C^{N/2} z=DFT(q⋅μ)⋅2τ∈CN/2
-
Add(同态的 M M M 上的加法):
- 输入密文 ( c 1 , τ 1 , L 1 ) (c_1,\tau_1,L_1) (c1,τ1,L1) 和 ( c 2 , τ 2 , L 2 ) (c_2,\tau_2,L_2) (c2,τ2,L2)
- 统一指数 τ = max ( τ 1 , τ 2 ) + 1 \tau = \max(\tau_1,\tau_2)+1 τ=max(τ1,τ2)+1
- 统一层数 L = min ( L 1 + τ 1 , L 2 + τ 2 ) − τ L=\min(L_1+\tau_1,L_2+\tau_2)-\tau L=min(L1+τ1,L2+τ2)−τ
- 加和 c = 2 τ 1 + L 1 − ( τ + L ) c 1 + 2 τ 2 + L 2 − ( τ + L ) c 2 ( m o d Z ) c=2^{\tau_1+L_1-(\tau+L)}c_1 + 2^{\tau_2+L_2-(\tau+L)}c_2 \pmod{\mathbb Z} c=2τ1+L1−(τ+L)c1+2τ2+L2−(τ+L)c2(modZ)
-
Decrease level(模切换/重缩放过程):
- 输入密文 ( c , τ , L ) (c,\tau,L) (c,τ,L) 和层数 1 ≤ L ′ < L 1 \le L'<L 1≤L′<L
- 输出 ( 2 L − L ′ c , τ , L ′ ) (2^{L-L'}c, \tau,L') (2L−L′c,τ,L′)
-
Binary Shift(二的幂次):
- 输入密文 ( c , τ , L ) (c,\tau,L) (c,τ,L) 和移位距离 t ∈ N t \in \mathbb N t∈N
- 输出 ( c , τ + t , L ) (c, \tau+t,L) (c,τ+t,L)
-
Mult by constant( Z \mathbb Z Z 模 T R \mathbb T_R TR):
- 输入密文 ( c , τ , L ) (c,\tau,L) (c,τ,L) 和常数 a ∈ Z a \in \mathbb Z a∈Z
- 输出 ( a ⋅ c , τ + ρ , L − ρ ) (a \cdot c, \tau+\rho,L-\rho) (a⋅c,τ+ρ,L−ρ)
-
Slot-wise Mult by constant( R R R 模 T R \mathbb T_R TR):
- 输入密文 ( c , τ , L ) (c,\tau,L) (c,τ,L) 和有限精度复数 u = ( u 1 , ⋯ , u N / 2 ) ∈ C N / 2 u=(u_1,\cdots,u_{N/2}) \in \mathbb C^{N/2} u=(u1,⋯,uN/2)∈CN/2
- 找出多项式 d ( x ) ∈ R d(x) \in R d(x)∈R,系数取值范围 [ − 2 ρ , 2 ρ ] [-2^\rho,2^\rho] [−2ρ,2ρ],以及对应的指数 t ∈ Z t \in \mathbb Z t∈Z,满足 ∥ D F T ( d ) ⋅ 2 t − u ∥ ∞ ≤ 2 t − ρ \|DFT(d) \cdot 2^t - u\|_\infty \le 2^{t-\rho} ∥DFT(d)⋅2t−u∥∞≤2t−ρ
- 输出 ( d ( x ) ⋅ c , τ + ρ + t , L − ρ ) (d(x) \cdot c, \tau+\rho+t, L-\rho) (d(x)⋅c,τ+ρ+t,L−ρ)
-
External Product:
- 将上述的 d ( x ) ∈ R d(x) \in R d(x)∈R 用 TRGSW 预加密为 T R G S W s , α ( d ) TRGSW_{s,\alpha}(d) TRGSWs,α(d)
- 计算 T R G S W s , α ( d ) ⊡ α c TRGSW_{s,\alpha}(d) \boxdot_\alpha c TRGSWs,α(d)⊡αc
-
Internal multiplication:
- 输入密文 ( c 1 , τ 1 , L 1 ) (c_1,\tau_1,L_1) (c1,τ1,L1) 和 ( c 2 , τ 2 , L 2 ) (c_2,\tau_2,L_2) (c2,τ2,L2)
- 统一层数 L ′ = min ( L 1 , L 2 ) L'=\min(L_1,L_2) L′=min(L1,L2),执行 c i ′ = R S L i → L ′ ( c i ) c_i'=RS_{L_i \to L'}(c_i) ci′=RSLi→L′(ci)
- 设置模数 q = 2 L ′ + ρ q=2^{L'+\rho} q=2L′+ρ,密文精度 α = 1 / q \alpha=1/q α=1/q
- 将 c i ′ c_i' ci′ 园整到 α R / R \alpha R/R αR/R(密文的浮点表示的尾数截断到 L ′ + ρ L'+\rho L′+ρ 比特)
- 计算 BFV 内积 c = c 1 ′ ⊡ q , α c 2 ′ c=c_1' \boxdot_{q,\alpha} c_2' c=c1′⊡q,αc2′
- 层数 L = L ′ − ρ L=L'-\rho L=L′−ρ,指数 τ = τ 1 ⋅ τ 2 \tau = \tau_1 \cdot \tau_2 τ=τ1⋅τ2
- 输出 ( c , τ , L ) (c,\tau,L) (c,τ,L),如果 ρ ≥ log N \rho \ge \log N ρ≥logN 那么 V a r ( E r r ( c ) ) ≤ 4 − ( L + ρ ) Var(Err(c)) \le 4^{-(L+\rho)} Var(Err(c))≤4−(L+ρ)(噪声在 2 − ( L + ρ ) R / R 2^{-(L+\rho)}R/R 2−(L+ρ)R/R 中完全隐藏)
现在 CKKS 的明文是 μ ∈ 2 − ( L + ρ ) R / R ⊆ T R \mu \in 2^{-(L+\rho)}R/R \subseteq \mathbb T_R μ∈2−(L+ρ)R/R⊆TR,密文是 c = ( a , b ) ∈ T R 2 c=(a,b) \in \mathbb T_R^2 c=(a,b)∈TR2,它们与 TRLWE 的明密文空间相兼容。
CKKS to TFHE
由于
L
=
1
L=1
L=1 时,所加密的 native 明文为
μ
=
d
/
2
ρ
+
1
\mu=d/2^{\rho+1}
μ=d/2ρ+1,设置
q
=
2
ρ
+
1
q=2^{\rho+1}
q=2ρ+1,它诱导了双射
d
i
=
q
⋅
μ
i
∈
[
−
2
ρ
,
2
ρ
)
→
μ
i
∈
[
−
0.5
,
0.5
)
∩
q
−
1
Z
/
Z
d_i=q \cdot\mu_i \in [-2^\rho,2^\rho) \to \mu_i \in [-0.5,0.5) \cap q^{-1}\mathbb Z/\mathbb Z
di=q⋅μi∈[−2ρ,2ρ)→μi∈[−0.5,0.5)∩q−1Z/Z
因此,这个 coeff packing 的 CKKS 密文恰好就是 TFHE 密文。
转换算法为:
- 先执行 Slot to Coeff 过程,得到两个 coeff packing 的密文 ( c 1 , c 2 ) ← M a t M u l t ( c , I D F T ) (c_1,c_2) \gets MatMult(c,IDFT) (c1,c2)←MatMult(c,IDFT)
- 然后做重缩放, c i ′ = R S L ′ → 1 ( c i ) c_i' = RS_{L' \to 1}(c_i) ci′=RSL′→1(ci) 成为 TRLWE 密文
- 最后使用 Sample Extract,提取出各个系数的 TLWE 密文(还需要记录它们的指数 τ \tau τ)
TFHE to CKKS
从 TFHE 到 CKKS 的转换过程,
- 输入 N / 2 N/2 N/2 个消息 v k ∈ T v_k \in \mathbb T vk∈T 的 TLWE 密文,
- 输出单个 slot packing 编码的消息 exp ( 2 π i ⋅ v k ) \exp(2\pi i \cdot v_k) exp(2πi⋅vk) 的 TRLWE 密文
有些类似于 [CHKKS18] 的 CKKS Boostrpping Trick,[BGGJ20] 使用傅里叶级数来近似指数函数。根据 Taylor–Lagrange 不等式,
∣
exp
(
i
x
)
−
∑
k
=
0
t
−
1
(
i
x
)
k
k
!
∣
≤
∣
x
∣
t
t
!
\left| \exp(i x) - \sum_{k=0}^{t-1} \dfrac{(i x)^k}{k!} \right| \le \dfrac{|x|^t}{t!}
exp(ix)−k=0∑t−1k!(ix)k
≤t!∣x∣t
我们希望以精度
2
−
ρ
2^{-\rho}
2−ρ 近似指数函数,设置泰勒级数的项数为
t
=
ρ
t=\sqrt \rho
t=ρ。如果我们约束
x
≤
n
/
2
p
x \le n/2^p
x≤n/2p,选择足够大的
p
=
ρ
+
log
(
2
π
n
/
ρ
)
p = \sqrt\rho + \log(2\pi n/\sqrt \rho)
p=ρ+log(2πn/ρ)
就可以满足 2 − ρ 2^{-\rho} 2−ρ 的精度要求。
为了计算 exp ( 2 π i ⋅ v ) \exp(2\pi i \cdot v) exp(2πi⋅v),
- 首先对相位 ϕ s ( c ) = v \phi_s(c)= v ϕs(c)=v 做恰当的缩放,得到 x = 2 π v / 2 p ≤ n / 2 p x=2\pi v/2^p \le n/2^p x=2πv/2p≤n/2p
- 然后使用 Paterson–Stockmayer 多项式求值算法,计算前 t t t 项泰勒级数(度数 t = ρ t=\sqrt \rho t=ρ 的多项式),得到 E = exp ( 2 π i ⋅ v / 2 p ) E=\exp(2\pi i \cdot v/2^p) E=exp(2πi⋅v/2p)
- 最后使用快速幂算法,计算出 exp ( 2 π i ⋅ v ) = E 2 p \exp(2\pi i \cdot v) = E^{2^p} exp(2πi⋅v)=E2p

现在,我们有两种计算非线性函数的方法:
- 使用常规同态乘法,以 SIMD 的方式计算复数多项式
- 在自举过程中,利用三角函数(傅里叶级数是个较好的选择,收敛速度快)去逼近
方案切换的总结
[ABB+22] 实现了 OpenFHE 工具包,它还没有实现 Scheme Switching,但是给出了一些有用的观察:
- 在 BGV 和 BFV 之间的转换是平凡的,使用 [AP13] 的 LSB 和 MSB 转换技术
- 在 FHEW 和 TFHE 之间,根本就不需要转换,它们只有自举过程是不同的
- 从 BGV-like 到 FHEW-like,只需要执行 solt to coeff 过程,必要时使用 Key / Modulus Switching,但是一般不需要 Bootstrapping
- 从 FHEW-like 到 BGV-like,需要用自举来减小噪声比率,其中 CKKS 只需要轻量级的自举变体
- 而 BGV/BFV 和 CKKS 之间的转换,两个方向上都需要完全的自举
- 秘钥切换过程,可以视为 Functional Scheme Switch 的特例,源 / 目标是秘钥不同的相同方案

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献12条内容
已为社区贡献12条内容





所有评论(0)