如何更科学地规划刚体姿态？Planning with Attitude论文阅读笔记

Planning with AttitudeJackson, Brian E. et al. “Planning With Attitude.” IEEE Robotics and Automation Letters 6 (2021): 5658-5664.https://roboticexplorationlab.org/papers/planning_with_attitude.pdfhtt

Peiy_Liu

89人浏览 · 2023-09-03 14:44:30

Peiy_Liu · 2023-09-03 14:44:30 发布

Planning with Attitude

Jackson, Brian E. et al. “Planning With Attitude.” IEEE Robotics and Automation Letters 6 (2021): 5658-5664.

https://roboticexplorationlab.org/papers/planning_with_attitude.pdf

https://github.com/RoboticExplorationLab/PlanningWithAttitude

概述

Motivation：由于3D旋转群SE(3)的非平凡结构，为那些会有大的姿态变化的floating-based机器人系统规划轨迹是一件有挑战性的事。
本文提出了一种只用标准线代和向量微积分即可在旋转空间上进行optimization-based规划的强大方法

Introduction

Background

痛点：平移的表示很直接且很符合直觉的，但要有效地表示具有非平凡群结构的3D旋转就比较有挑战性了。即使我们可以很直接地得出旋转是3维的，我们也无法为旋转空间找到一个全局非奇异的3维参数化表达。

当参数化旋转时，我们：

either：用3维参数化表达，并处理奇异性和非连续性；
or：选择一个更高维的表达，并处理参数间的约束。（如单位四元数）

参数化旋转是个非平凡的问题，而生成和跟踪带旋转的运动更有挑战性。

Related Works

带有旋转群的控制问题
带有旋转群的轨迹生成、sampling-based运动规划和最优控制

Contributions

提出了一种完全基于标准线性代数和向量微积分的四元数微积分方法
推导出一个直接在单位四元数空间上进行的Newton-based非线性优化算法
实现了一个快速高效的、正确处理3D旋转的群结构的、求解带姿态动力学和非线性约束的轨迹优化问题的求解器

Background

单位四元数的一些性质

一些单位四元数的基本性质省略。

另外一些本文用到的性质：

共轭：

$q^* = Tq := \begin{bmatrix} 1 & \\ & -I_3\end{bmatrix}q$

共轭与乘法矩阵

$\begin{aligned} &L(Tq) = L^\top(q)=L^{-1}(q) \\ &R(Tq) = R^\top(q)=R^{-1}(q)\end{aligned}$

3维向量 $\in \mathbb{R}^3$ 对应的纯四元数：

$\hat{r} = Hr = \begin{bmatrix}0 \\ I_3 \end{bmatrix}r$

纯四元数 $\hat{r} \in \mathbb{R}^4$ 对应的3维向量：

$H^\top \hat{r}$

四元数旋转 $\hat{r}' = q \otimes \hat{r} \otimes q^*$ 的矩阵表达：

$H^\top L(q)R^\top(q)Hr = A(q)r$

这里的 $A (q)$ 就是旋转矩阵了。

刚体动力学

在这里插入图片描述

Quaternion Differential Calculus

在这里插入图片描述

本节考虑的问题： 单位四元数函数的导数怎么定义？

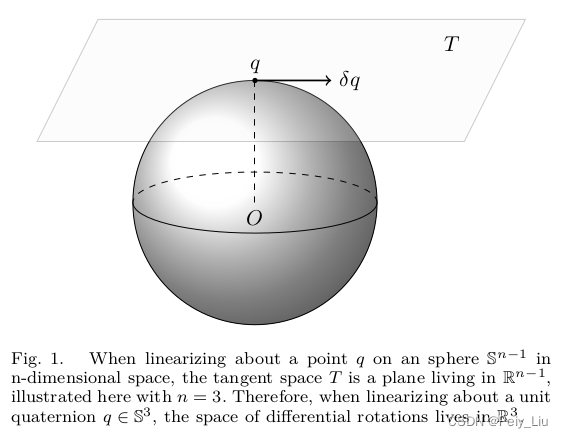
定义导数时有这样一个事实：对输入的无穷小扰动会造成对输出的无穷小扰动

对向量空间：扰动的施加方式就是普通的加法，并且无穷小扰动与original vector是在同一个空间内。
对单位四元数：扰动的施加方式是四元数乘法，并且无穷小单位四元数扰动是与该点3维切空间局部同构的（如上图所示），显然，四元数微分就是3维的。

微小旋转的参数化

文中采用Cayley map (Rodrigues parameters)：

$\varphi(\phi) = \frac{1}{\sqrt{1+\Vert\phi\Vert^2}}\begin{bmatrix}1 \\ \phi\end{bmatrix}$

采用该参数化方式的好处是计算效率高且没有单位四元数的符号歧义。

逆映射：

$\phi = \varphi^{-1}(q) = \frac{q_v}{q_s}$

向量值函数的Jacobian

考虑向量值四元数函数 $\mathbb{S}^3 \rightarrow \mathbb{R}^p$ ，对于微小扰动 $\delta \phi$ ，我们有：

$\delta y = h(L(q)\varphi(\delta\phi)) \approx h(q) + \nabla h(q)\delta\phi$

则 $h$ 对扰动 $\delta\phi$ 的Jacobian $\nabla h(q) \in \mathbb{R}^{p\times 3}$ 为：

$\nabla h(q) = \frac{\partial h}{\partial q}L(q)H := \frac{\partial h}{\partial q}G(q) = \frac{\partial h}{\partial q} \begin{bmatrix} -q_v^\top \\ q_s I_3 + [q_v]_\times \end{bmatrix}$

As an aside, although we have used Rodrigues parameters, $G (q)$ is actually the same (up to a constant scalar factor) for any choice of three-parameter attitude representation.

注意：

$\in \mathbb{R}^{4 \times 3}$ 称为attitude Jacobian
对于任意 $\in \mathbb{R}^3$ ，有如下性质：

$\otimes v \iff v = H^\top(q^* \otimes q') = H^\top L^\top(q)q' = G^\top(q)q'$

特别地，对于 $h (q) = q$ ，有：

$\delta q = I_4G(q)\delta\phi + \omicron(\delta\phi) = G(q)\delta\phi + \omicron(\delta\phi)$

以上两条性质由自己推导得出，论文中并未直接说明

标量值数的Hessian

在这里插入图片描述

Quaternion-Valued函数的Jacobian

考虑一个Quaternion-Valued函数 $\mathbb{S}^3 \rightarrow \mathbb{S}^3$ ，其Jacobian为：

在这里插入图片描述

Modifying Newton’s Method

本节主要是基于之前的理论对传统naïve Newton法作修改。

传统的Newton法在优化变量带单位四元数时需要在update步骤时用普通加法不能保证单位四元数的范数约束，需要将update后的四元数投影回单位四元数平面。

本文修改后的Newton法用3维参数化和四元数乘法的方式更新四元数，保证了四元数的范数约束。

Methodology

研究对象：Wahba‘s Problem，一种最小二乘姿态估计问题。

在这里插入图片描述

思路：
- update值的表征：用3维参数化：
$\phi_k = -(\nabla r^\top \nabla r)^{-1}\nabla r^\top r(q_k)$
- update值的施加：用四元数乘法：
$q_{k+1} = q_k \otimes \varphi(\phi_k)$
方法：基于上述思路得到用于求解Wahba’s problem (19)的Multiplicative Gauss-Newton Method：

在这里插入图片描述

对比：文章将上述提出的Multipilicative Gauss-Newton方法与naïve Newton方法在Wahba’s problem上做了比较，结果如下：
- 如下图所示naïve Newton方法一开始可以有效使目标函数值下降，但很快就停滞了；
- multiplicative方法因为正确处理了群结构，因此得以保持Newton法典型的快速收敛；
- 对比用SVD方法求解出的全局解，可以看到本文提出的multiplicative方法可以在很小的迭代次数后收敛到全局最优解。

在这里插入图片描述

Trajectory Optimization for Rigid Bodies

本文对轨迹优化求解器ALTRO进行了修改，使之能够求解任意状态空间为 $\mathbb{R}^n \times \mathbb{S}^3$ 的系统的轨迹优化问题。

轨迹优化问题的形式：

$\begin{aligned} &\min_{x_{1:N}, u_{1:N-1}} &l_f(x_N) + \sum_{k=1}^{N-1}l_k(x_k, u_k) \\ & s.t. & x_{k+1} = f(x_k, u_k), \\ & &g_k(x_k,u_k)\leq0, \\ & &h_k(x_k, u_k) = 0\end{aligned}$

对一个刚体系统，我们定义其状态变量为：

$x_k = \begin{bmatrix} r_k \\ q_k \\ v_k \\ \omega_k \end{bmatrix} \in \mathbb{R}^{13}$

误差状态为：

$\delta x_k = \begin{bmatrix} r_k - \bar{r}_k \\ \varphi^{-1}(\bar{q}_k^{-1}\otimes q_k) \\ v_k - \bar{v}_k \\ \omega_k - \bar{\omega}_k \end{bmatrix} \in \mathbb{R}^{12}$

令 $\Delta x_k = x_k - \bar{x}_k \in \mathbb{R}^{13}$ ， $\delta\phi_k = \varphi^{-1}(\bar{q}_k^{-1}\otimes q_k)$ ，对于姿态部分根据之前结论有：

$\Delta q_k = G(q_k)\delta\phi_k + \omicron(\delta\phi_k)$

则

$\Delta x_k = E(x_k)\delta x_k + \begin{bmatrix} 0 \\ \omicron(\delta\phi_k) \\ 0 \\ 0 \end{bmatrix}, E(x_k) = \begin{bmatrix} I_3 & 0 & 0 & 0 \\ 0 & G(q_k) & 0 & 0 \\ 0 & 0 & I_3 & 0 \\ 0 & 0 & 0 & I_3 \end{bmatrix}$

对轨迹优化问题约束中的系统方程在期望值 $(\bar{x}_k, \bar{u}_k)$ 处进行一阶Taylor展开：

$\begin{aligned} x_{k+1} &= f(\bar{x}_k, \bar{u}_k) + \frac{\partial f}{\partial x}\vert_{(\bar{x}_k, \bar{u}_k)}(x_k - \bar{x}_k) + \frac{\partial f}{\partial u}\vert_{(\bar{x}_k, \bar{u}_k)}(u_k - \bar{u}_k) + \omicron(\Delta x_k, \Delta u_k) \\ &= \bar{x}_{k+1} + \frac{\partial f}{\partial x}\vert_{(\bar{x}_k, \bar{u}_k)}\Delta x_k + \frac{\partial f}{\partial u}\vert_{(\bar{x}_k, \bar{u}_k)}\Delta u_k + \omicron(\Delta x_k, \Delta u_k)\end{aligned}$

移项并省略高阶无穷小得到

$E(x_{k+1})\delta x_{k+1} = \frac{\partial f}{\partial x}\vert_{(\bar{x}_k, \bar{u}_k)}E(x_k)\delta x_k + \frac{\partial f}{\partial u}\vert_{(\bar{x}_k, \bar{u}_k)}\delta u_k$

结合先前的结论得到系统方程在期望值 $(\bar{x}_k, \bar{u}_k)$ 处线性化后的误差状态模型：

$\delta x_{k+1} = A_k \delta x_k + B_k \delta u_k$

其中：

$\begin{aligned} &A_k = E^\top(x_{k+1})\frac{\partial f}{\partial x}\vert_{(\bar{x}_k, \bar{u}_k)}E(x_k) \\ &B_k = E^\top(x_{k+1})\frac{\partial f}{\partial u}\vert_{(\bar{x}_k, \bar{u}_k)} \end{aligned}$

对于标准的Newton或quasi-Newton方法，我们可以计算cost function的二阶展开：

$\delta l(x,u) \approx \frac{1}{2}\delta x^\top l_{xx} \delta x + \frac{1}{2}\delta u^\top l_{uu} \delta u + \delta u^\top l_{ux} \delta x + l_x^\top \delta x + l_u^\top\delta u$

对于基于DDP和LQR的方法（不熟悉，暂时略写），我们可以计算：

在这里插入图片描述

复现与测试

在PnP问题中Multipicative Gauss-Newton与传统Gauss-Newton方法对比

Jacobian推导

特征点在相机系中的坐标:

$P_c = \begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix} = R(q)P + t$

其中 $P$ 为特征点的世界坐标， $R (q)$ 和 $t$ 代表相机位姿。

残差：

$\begin{bmatrix} \Delta u \\ \Delta v \end{bmatrix} = \begin{bmatrix} u - f_x \frac{X_c}{Z_c} - c_x \\ v - f_y \frac{Y_c}{Z_c} - c_y \end{bmatrix}$

残差对 $P_c$ 的Jacobian：

$\frac{\partial e}{\partial P_c} = \begin{bmatrix} -\frac{f_x}{Z_c} & 0 & f_x\frac{X_c}{Z_c^2} \\ 0 & -\frac{f_y}{Z_c} & f_y\frac{Y_c}{Z_c^2} \end{bmatrix}$

$P_c$ 对姿态四元数 $q$ 的Jacobian：

$\frac{\partial P_c}{\partial q} = 2 H^\top [q]_\mathcal{R}^\top [HP]_\mathcal{R} \in \mathbb{R}^{3\times4}$

残差对姿态扰动 $\delta\phi$ （采用Rodrigues parameterization）的Jacobian：

$\frac{\partial e}{\partial \delta \phi} = \frac{\partial e}{\partial q} G(q) = \frac{\partial e}{\partial P_c} \frac{\partial P_c}{\partial q} G(q) = \frac{\partial e}{\partial P_c} \frac{\partial P_c}{\partial q}[q]_\mathcal{L}H\in \mathbb{R}^{2\times3}$

残差对位置的Jacobian：

$\frac{\partial e}{\partial t} = \frac{\partial e}{\partial P_c} \frac{\partial P_c}{\partial t} = \frac{\partial e}{\partial P_c} I_3 = \frac{\partial e}{\partial P_c} \in \mathbb{R}^{2\times3}$

则残差对位姿的Jacobian：

代码实现

在十四讲的ch7代码中实现了Multipicative Gauss-Newton方法：

void bundleAdjustmentMultipicativeGaussNewton(const VecVector3d &points_3d, 
                                              const VecVector2d &points_2d, 
                                              const cv::Mat &K, 
                                              Eigen::Quaterniond &q, 
                                              Eigen::Vector3d &t)
{
    typedef Eigen::Matrix<double, 6, 1> Vector6d;

    const int iter_num = 10;
    double cost = 0.0, last_cost = 0.0;
    double fx = K.at<double>(0, 0);
    double fy = K.at<double>(1, 1);
    double cx = K.at<double>(0, 2);
    double cy = K.at<double>(1, 2);

    Eigen::Matrix<double, 4, 3> H = Eigen::Matrix<double, 4, 3>::Zero();
    H.block<3, 3>(1, 0).setIdentity();
    Eigen::Matrix<double, 3, 4> Ht = H.transpose();

    for (int iter = 0; iter < iter_num; ++iter)
    {
        Eigen::Matrix<double, 6, 6> D = Eigen::Matrix<double, 6, 6>::Zero();
        Vector6d b = Vector6d::Zero();

        cost = 0;
        for (int i = 0; i < points_3d.size(); ++i)
        {
            Eigen::Vector3d pc = q * points_3d[i] + t;
            double inv_z = 1.0 / pc.z();
            double inv_z2 = inv_z * inv_z;
            double x = pc.x(), y = pc.y();
            Eigen::Vector2d proj(fx * x * inv_z + cx, 
                                 fy * y * inv_z + cy);
            
            // compute cost
            Eigen::Vector2d e = points_2d[i] - proj;
            cost += e.squaredNorm();

            // compute Jacobian
            Eigen::Matrix<double, 2, 6> J;
            Eigen::Matrix<double, 2, 3> de_dpc;
            Eigen::Matrix<double, 3, 6> dpc_dpose;
            Eigen::Matrix<double, 4, 3> dq_dphi = leftQ(q) * H;

            de_dpc << -fx * inv_z, 0.0, fx * x * inv_z2, 
                      0.0, -fy * inv_z, fy * y * inv_z2;
            dpc_dpose.block<3, 3>(0, 0) = 2.0 * Ht * rightQ(q).transpose() * rightQ(H * points_3d[i]) * dq_dphi;
            dpc_dpose.block<3, 3>(0, 3).setIdentity();
            J = de_dpc * dpc_dpose;

            D += J.transpose() * J;
            b += -J.transpose() * e;
        }

        Vector6d dx = D.ldlt().solve(b);

        if (std::isnan(dx[0]))
        {
            std::cout << "Result is NaN!" << std::endl;
            break;
        }

        if (iter > 0 && cost >= last_cost)
        {
            std::cout << "cost: " << cost << ", last cost: " << last_cost << std::endl;
            break;
        }

        // update
        Eigen::Vector4d delta_q = CayleyMap(dx.head<3>());
        q *= Eigen::Quaterniond(delta_q(0), delta_q(1), delta_q(2), delta_q(3));
        t += dx.tail<3>();
        last_cost = cost;

        std::cout << "iteration " << iter << " cost = " << std::cout.precision(12) << cost << std::endl;
        if (dx.norm() < 1e-6)
        {
            break;
        }
    }
    Sophus::SE3d pose(q, t);
    std::cout << "Pose estimated by Multiplicative G-N: \n" << pose.matrix() << std::endl;
}

传统（常用的）Gauss-Newton法：

void bundleAdjustmentGaussNewton(const VecVector3d &points_3d, 
                                 const VecVector2d &points_2d, 
                                 const cv::Mat &K, 
                                 Sophus::SE3d &pose)
{
    typedef Eigen::Matrix<double, 6, 1> Vector6d;

    const int iter_num = 10;
    double cost = 0.0, last_cost = 0.0;
    double fx = K.at<double>(0, 0);
    double fy = K.at<double>(1, 1);
    double cx = K.at<double>(0, 2);
    double cy = K.at<double>(1, 2);

    for (int iter = 0; iter < iter_num; ++iter)
    {
        Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();
        Vector6d b = Vector6d::Zero();

        cost = 0;
        for (int i = 0; i < points_3d.size(); ++i)
        {
            Eigen::Vector3d pc = pose * points_3d[i];
            double inv_z = 1.0 / pc.z();
            double inv_z2 = inv_z * inv_z;
            double x = pc.x(), y = pc.y();
            Eigen::Vector2d proj(fx * x * inv_z + cx, 
                                 fy * y * inv_z + cy);
            
            // compute cost
            Eigen::Vector2d e = points_2d[i] - proj;
            cost += e.squaredNorm();

            // compute Jacobian
            Eigen::Matrix<double, 2, 6> J;
            J << -fx * inv_z, 
                 0, 
                 fx * x * inv_z2, 
                 fx * x * y * inv_z2, 
                 -fx - fx * x * x * inv_z2, 
                 fx * y * inv_z, 
                 0, 
                 -fy * inv_z, 
                 fy * y * inv_z2, 
                 fy + fy * y * y * inv_z2, 
                 -fy * x * y * inv_z2, 
                 -fy * x * inv_z;

            H += J.transpose() * J;
            b += -J.transpose() * e;
        }

        Vector6d dx = H.ldlt().solve(b);

        if (std::isnan(dx[0]))
        {
            std::cout << "Result is NaN!" << std::endl;
            break;
        }

        if (iter > 0 && cost >= last_cost)
        {
            std::cout << "cost: " << cost << ", last cost: " << last_cost << std::endl;
            break;
        }

        // update
        pose = Sophus::SE3d::exp(dx) * pose;
        last_cost = cost;

        std::cout << "iteration " << iter << " cost = " << std::cout.precision(12) << cost << std::endl;
        if (dx.norm() < 1e-6)
        {
            break;
        }
    }
    std::cout << "Pose estimated by G-N: \n" << pose.matrix() << std::endl;
}

运行结果

Multipicative Gauss-Newton方法：

--------------------Multiplicative Gauss-Newton--------------------
iteration 0 cost = 1240517.7576706
iteration 1 cost = 12328.016744741
iteration 2 cost = 12299.763719166
iteration 3 cost = 12299.763574327
Pose estimated by Multiplicative G-N: 
   0.997905909552   -0.050919400915   0.0398874703697   -0.126782138844
    0.04981866257    0.998362315744   0.0281209417082 -0.00843949674217
 -0.0412540487924  -0.0260749134857    0.998808391207   0.0603493574703
                0                 0                 0                 1
Pose estimation using Multiplicative G-N cost time: 0.000113559second(s)
R = 
  0.997905909552  -0.050919400915  0.0398874703697
   0.04981866257   0.998362315744  0.0281209417082
-0.0412540487924 -0.0260749134857   0.998808391207
t = 
  -0.126782138844
-0.00843949674217
  0.0603493574703

传统Gauss-Newton方法：

--------------------Gauss-Newton--------------------
iteration 0 cost = 640517.7576706
iteration 1 cost = 12410.547029116
iteration 2 cost = 12299.76468142
iteration 3 cost = 12299.763574327
Pose estimated by G-N: 
   0.997905909549  -0.0509194008562   0.0398874705187   -0.126782139096
   0.049818662505    0.998362315745   0.0281209417649 -0.00843949683874
 -0.0412540489424  -0.0260749135374    0.998808391199   0.0603493575229
                0                 0                 0                 1
Pose estimation using G-N cost time: 9.4544e-05second(s)
R = 
  0.997905909549 -0.0509194008562  0.0398874705187
  0.049818662505   0.998362315745  0.0281209417649
-0.0412540489424 -0.0260749135374   0.998808391199
t = 
  -0.126782139096
-0.00843949683874
  0.0603493575229

可以看到在这个PnP问题中，二者区别并不大。

在形式上区别主要在于：