slam十四讲复习
由于书上讲的比较清楚,此处仅记录重点知识,梳理相关代码。1.环境配置1.1 cmake1.1.1 基本使用最基础的cmake 相关指令:project() 与 add_executable# 声明要求的 cmake 最低版本cmake_minimum_required( VERSION 2.8 )# 声明一个 cmake 工程project( HelloSLAM )# 添加一个可执行程序# 语法:
由于书上讲的比较清楚,此处仅记录重点知识,梳理相关代码。
1.环境配置
1.1 cmake
1.1.1 基本使用
- 最基础的cmake 相关指令:project() 与 add_executable
# 声明要求的 cmake 最低版本
cmake_minimum_required( VERSION 2.8 )
# 声明一个 cmake 工程
project( HelloSLAM )
# 添加一个可执行程序
# 语法:add_executable( 程序名 源代码文件 )
add_executable( helloSLAM helloSLAM.cpp )
- 相关使用
mkdir build
cd build
cmake ..
make
1.1.2 生成库
将add_executable替换成add_library(.a后缀)
add_library( hello libHelloSLAM.cpp )
如果生成共享库(.so后缀)
add_library( hello_shared SHARED libHelloSLAM.cpp )
除了库文件,还需要提供一个头文件.头文件和库文件需要同时提供给用户
1.1.3 使用库
- 如果库与源代码在同一个位置下
add_executable( useHello useHello.cpp )
target_link_libraries( useHello hello_shared )
- 如果库与源代码不在同一个位置下
1.2 IDE Kdevelop
见34
2.知识部分
2.1 基础数学知识
2.1.1 外积的表示
p42
- 对于向量引入运算^,该运算表示
[ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] \left[\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}\right] ⎣⎡0a3−a2−a30a1a2−a10⎦⎤
从而 a × b a\times b a×b= a a a^ b b b - 坐标系之间的欧式变换
[ e 1 , e 2 , e 3 ] [ a 1 a 2 a 3 ] = [ e 1 ′ , e 2 ′ , e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] ⇒ [ a 1 a 2 a 3 ] = [ e 1 T e 1 ′ e 1 T e 2 ′ e 1 T e 3 ′ e 2 T e 1 ′ e 2 T e 2 ′ e 2 T e 3 ′ e 3 T e 1 ′ e 3 T e 2 ′ e 3 T e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] ≜ R a ′ \left[e_{1}, e_{2}, e_{3}\right]\left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[e_{1}^{\prime}, e_{2}^{\prime}, e_{3}^{\prime}\right]\left[\begin{array}{c} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right]\Rightarrow\\ \left[\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[\begin{array}{lll} e_{1}^{T} e_{1}^{\prime} & e_{1}^{T} e_{2}^{\prime} & e_{1}^{T} e_{3}^{\prime} \\ e_{2}^{T} e_{1}^{\prime} & e_{2}^{T} e_{2}^{\prime} & e_{2}^{T} e_{3}^{\prime} \\ e_{3}^{T} e_{1}^{\prime} & e_{3}^{T} e_{2}^{\prime} & e_{3}^{T} e_{3}^{\prime} \end{array}\right]\left[\begin{array}{l} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right] \triangleq \boldsymbol{R} \boldsymbol{a}^{\prime} [e1,e2,e3]⎣⎡a1a2a3⎦⎤=[e1′,e2′,e3′]⎣⎡a1′a2′a3′⎦⎤⇒⎣⎡a1a2a3⎦⎤=⎣⎡e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′⎦⎤⎣⎡a1′a2′a3′⎦⎤≜Ra′
中间的矩阵记为R,其中 R − 1 = R T R^{-1}=R^T R−1=RT
2.1.2 齐次坐标与特殊欧式群
p46
- 齐次坐标下的变化可以表示成特殊欧式群中的元素
S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } S E(3)=\left\{T=\left[\begin{array}{cc} R & t \\ 0^{T} & 1 \end{array}\right] \in \mathbb{R}^{4 \times 4} \mid R \in S O(3), t \in \mathbb{R}^{3}\right\} SE(3)={T=[R0Tt1]∈R4×4∣R∈SO(3),t∈R3}
2.1.3 旋转向量与欧拉角
p50
2.1.3.1 旋转向量
- 起因:SO(3)的旋转矩阵有九个量,但是一次旋转只有三个自由度;同时旋转矩阵自身带有约束,不利于求解
- 旋转向量:方向与旋转轴一致,而长度等于旋转角.事实上,旋转向量即使李代数.
2.1.3.2 罗德里格斯公式
-旋转向量到旋转矩阵的转换,公式为
R
=
cos
θ
I
+
(
1
−
cos
θ
)
n
n
T
+
sin
θ
n
∧
\boldsymbol{R}=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{n} \boldsymbol{n}^{T}+\sin \theta \boldsymbol{n}^{\wedge}
R=cosθI+(1−cosθ)nnT+sinθn∧
- 旋转矩阵到旋转向量的转换,公式为
tr ( R ) = cos θ tr ( I ) + ( 1 − cos θ ) tr ( n n T ) + sin θ tr ( n ∧ ) = 3 cos θ + ( 1 − cos θ ) = 1 + 2 cos θ \begin{aligned} \operatorname{tr}(\boldsymbol{R}) &=\cos \theta \operatorname{tr}(\boldsymbol{I})+(1-\cos \theta) \operatorname{tr}\left(\boldsymbol{n} \boldsymbol{n}^{T}\right)+\sin \theta \operatorname{tr}\left(\boldsymbol{n}^{\wedge}\right) \\ &=3 \cos \theta+(1-\cos \theta) \\ &=1+2 \cos \theta \end{aligned} tr(R)=cosθtr(I)+(1−cosθ)tr(nnT)+sinθtr(n∧)=3cosθ+(1−cosθ)=1+2cosθ
因此:
θ = arccos ( tr ( R ) − 1 2 ) \theta=\arccos \left(\frac{\operatorname{tr}(\boldsymbol{R})-1}{2}\right) θ=arccos(2tr(R)−1)
关于转轴 n n n, 由于旋转轴上的向量在旋转后不发生改变, 说明
R n = n R n=n Rn=n
因此,转轴 n n n 是矩阵 R R R 特征值 1 对应的特征向量。求解此方程, 再归一化, 就得到旋转轴
2.1.3.3 欧拉角
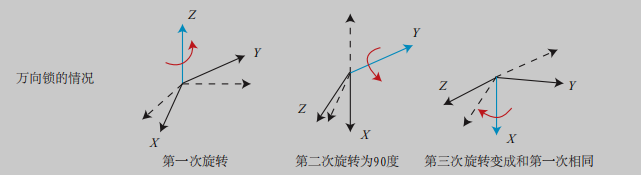
- 将旋转分解为三次绕不同轴的旋转,顺序为ZYX轴的旋转,三个角度为“偏航-俯仰-滚转”(yaw-pitch-roll)
用 [ r , p , y ] T [r,p,y]^T [r,p,y]T表示 - 万向锁问题:在俯仰角为±90◦ 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度.
(理论上来首,三个实数表示三维旋转都有该问题,所以欧拉角不适合插值和迭代,只能用于人机交互)
2.1.4 四元数
2.1.4.1 四元数定义
- 找不到不带奇异性的三维向量的描述方式(三维旋转是一个三维流形,想要无奇异性地表达它,三个量是不够的)
- 四元数是紧凑的,也没有奇异性
q = q 0 + q 1 i + q 2 j + q 3 k q=q_{0}+q_{1} i+q_{2} j+q_{3} k q=q0+q1i+q2j+q3k
其中 i , j , k i, j, k i,j,k 为四元数的三个虚部
{ i 2 = j 2 = k 2 = − 1 i j = k , j i = − k j k = i , k j = − i k i = j , i k = − j \left\{\begin{array}{l} i^{2}=j^{2}=k^{2}=-1 \\ i j=k, j i=-k \\ j k=i, k j=-i \\ k i=j, i k=-j \end{array}\right. ⎩⎪⎪⎨⎪⎪⎧i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j
也可以表示成
q = [ s , v ] , s = q 0 ∈ R , v = [ q 1 , q 2 , q 3 ] T ∈ R 3 \boldsymbol{q}=[s, \boldsymbol{v}], \quad s=q_{0} \in \mathbb{R}, \boldsymbol{v}=\left[q_{1}, q_{2}, q_{3}\right]^{T} \in \mathbb{R}^{3} q=[s,v],s=q0∈R,v=[q1,q2,q3]T∈R3
这里, s s s 称为四元数的实部, 而 v v v 称为它的虚部。 - 旋转向量转换为
2.1.4.2 四元数的运算
- 乘法
- 共轭
- 模长
- 逆
- 数乘与点乘
2.1.4.3 四元数与旋转
- 单元四元数表示空间中的一个旋转,乘以i表示绕着i轴旋转了180度(虽然i^2=-1)
2.1.4.3.1 四元数表示旋转
首先, 把三维空间点用一个虚四元数来描述:
p
=
[
0
,
x
,
y
,
z
]
=
[
0
,
v
]
\boldsymbol{p}=[0, x, y, z]=[0, \boldsymbol{v}]
p=[0,x,y,z]=[0,v]
这相当于我们把四元数的三个虚部与空间中的三个轴相对应。然后, 参照式 (3.19), 用四 元数
q
q
q 表示这个旋转:
q
=
[
cos
θ
2
,
n
sin
θ
2
]
\boldsymbol{q}=\left[\cos \frac{\theta}{2}, \boldsymbol{n} \sin \frac{\theta}{2}\right]
q=[cos2θ,nsin2θ]
那么, 旋转后的点
p
′
p^{\prime}
p′ 即可表示为这样的乘积:
p
′
=
q
p
q
−
1
p^{\prime}=q p q^{-1}
p′=qpq−1
计算结果的实部为 0 , 故为纯虚四元数。其虚部的三个分量表 示旋转后
3
D
3 \mathrm{D}
3D 点的坐标。
2.1.4.3.2 四元数与旋转向量的转换
- 从旋转向量到四元数
q = [ cos θ 2 , n x sin θ 2 , n y sin θ 2 , n z sin θ 2 ] T \boldsymbol{q}=\left[\cos \frac{\theta}{2}, n_{x} \sin \frac{\theta}{2}, n_{y} \sin \frac{\theta}{2}, n_{z} \sin \frac{\theta}{2}\right]^{T} q=[cos2θ,nxsin2θ,nysin2θ,nzsin2θ]T - 从四元数到旋转响铃
{ θ = 2 arccos q 0 [ n x , n y , n z ] T = [ q 1 , q 2 , q 3 ] T / sin θ 2 \left\{\begin{array}{l} \theta=2 \arccos q_{0} \\ {\left[n_{x}, n_{y}, n_{z}\right]^{T}=\left[q_{1}, q_{2}, q_{3}\right]^{T} / \sin \frac{\theta}{2}} \end{array}\right. {θ=2arccosq0[nx,ny,nz]T=[q1,q2,q3]T/sin2θ
(旋转 2 π 2\pi 2π得到的是相反的四元数,虽然旋转到了原处)
2.1.4.3.3 四元数与旋转矩阵的转换
通过将四元数转换为旋转向量,再转换为矩阵需要计算arccos,太麻烦,通过下面的工作计算.
设四元数
q
=
q
0
+
q
1
i
+
q
2
j
+
q
3
k
q=q_{0}+q_{1} i+q_{2} j+q_{3} k
q=q0+q1i+q2j+q3k, 对应的旋转矩阵
R
R
R 为:
R
=
[
1
−
2
q
2
2
−
2
q
3
2
2
q
1
q
2
+
2
q
0
q
3
2
q
1
q
3
−
2
q
0
q
2
2
q
1
q
2
−
2
q
0
q
3
1
−
2
q
1
2
−
2
q
3
2
2
q
2
q
3
+
2
q
0
q
1
2
q
1
q
3
+
2
q
0
q
2
2
q
2
q
3
−
2
q
0
q
1
1
−
2
q
1
2
−
2
q
2
2
]
\boldsymbol{R}=\left[\begin{array}{ccc} 1-2 q_{2}^{2}-2 q_{3}^{2} & 2 q_{1} q_{2}+2 q_{0} q_{3} & 2 q_{1} q_{3}-2 q_{0} q_{2} \\ 2 q_{1} q_{2}-2 q_{0} q_{3} & 1-2 q_{1}^{2}-2 q_{3}^{2} & 2 q_{2} q_{3}+2 q_{0} q_{1} \\ 2 q_{1} q_{3}+2 q_{0} q_{2} & 2 q_{2} q_{3}-2 q_{0} q_{1} & 1-2 q_{1}^{2}-2 q_{2}^{2} \end{array}\right]
R=⎣⎡1−2q22−2q322q1q2−2q0q32q1q3+2q0q22q1q2+2q0q31−2q12−2q322q2q3−2q0q12q1q3−2q0q22q2q3+2q0q11−2q12−2q22⎦⎤
反之,由旋转矩阵到四元数的转换如下。假设矩阵为
R
=
{
m
i
j
}
,
i
,
j
∈
[
1
,
2
,
3
]
\boldsymbol{R}=\left\{m_{i j}\right\}, i, j \in[1,2,3]
R={mij},i,j∈[1,2,3], 其对 应的四元数
q
q
q 由下式给出:
q
0
=
tr
(
R
)
+
1
2
,
q
1
=
m
23
−
m
32
4
q
0
,
q
2
=
m
31
−
m
13
4
q
0
,
q
3
=
m
12
−
m
21
4
q
0
q_{0}=\frac{\sqrt{\operatorname{tr}(R)+1}}{2}, q_{1}=\frac{m_{23}-m_{32}}{4 q_{0}}, q_{2}=\frac{m_{31}-m_{13}}{4 q_{0}}, q_{3}=\frac{m_{12}-m_{21}}{4 q_{0}}
q0=2tr(R)+1,q1=4q0m23−m32,q2=4q0m31−m13,q3=4q0m12−m21
- 值得一提的是,由于 q \boldsymbol{q} q 和 − q -\boldsymbol{q} −q 表示同一个旋转, 事实上一个 R \boldsymbol{R} R 对应的四元数表示并 不是惟一的。
- 实际编程中,当 q 0 q_{0} q0 接近 0 时, 其余三个分量会非常大,导致解不稳定,此时我们 再考虑使用其他的方式进行转换。
2.1.4.3.4 四元数的运算
- 乘法:
q a q b = s a s b − x a x b − y a y b − z a z b + ( s a x b + x a s b + y a z b − z a y b ) i + ( s a y b − x a z b + y a s b + z a x b ) j + ( s a z b + x a y b − y b x a + z a s b ) k q a q b = [ s a s b − v a T v b , s a v b + s b v a + v a × v b ] \begin{aligned} \boldsymbol{q}_{a} \boldsymbol{q}_{b}=& s_{a} s_{b}-x_{a} x_{b}-y_{a} y_{b}-z_{a} z_{b} \\ &+\left(s_{a} x_{b}+x_{a} s_{b}+y_{a} z_{b}-z_{a} y_{b}\right) i \\ &+\left(s_{a} y_{b}-x_{a} z_{b}+y_{a} s_{b}+z_{a} x_{b}\right) j \\ &+\left(s_{a} z_{b}+x_{a} y_{b}-y_{b} x_{a}+z_{a} s_{b}\right) k \end{aligned}\\ \boldsymbol{q}_{a} \boldsymbol{q}_{b}=[s_as_b-\boldsymbol{v}_{a} ^T\boldsymbol{v}_{b},s_a\boldsymbol{v}_{b}+s_b\boldsymbol{v}_{a}+\boldsymbol{v}_{a}\times \boldsymbol{v}_{b}] qaqb=sasb−xaxb−yayb−zazb+(saxb+xasb+yazb−zayb)i+(sayb−xazb+yasb+zaxb)j+(sazb+xayb−ybxa+zasb)kqaqb=[sasb−vaTvb,savb+sbva+va×vb] - 共轭
四元数的共轭是把虚部取成相反数:
q a ∗ = s a − x a i − y a j − z a k = [ s a , − v a ] \boldsymbol{q}_{a}^{*}=s_{a}-x_{a} i-y_{a} j-z_{a} k=\left[s_{a},-\boldsymbol{v}_{a}\right] qa∗=sa−xai−yaj−zak=[sa,−va]
四元数共轭与自己本身相乘,会得到一个实四元数, 其实部为模长的平方:
q ∗ q = q q ∗ = [ s a 2 + v T v , 0 ] q^{*} \boldsymbol{q}=\boldsymbol{q} \boldsymbol{q}^{*}=\left[s_{a}^{2}+\boldsymbol{v}^{T} \boldsymbol{v}, \mathbf{0}\right] q∗q=qq∗=[sa2+vTv,0] - 逆
q − 1 = q ∗ / ∣ ∣ q ∣ ∣ 2 , ( q a q b ) − 1 = ( q b ) − 1 ( q a ) − 1 q^{-1}=q^*/||q||^2,(q_aq_b)^{-1}=(q_b)^{-1}(q_a)^{-1} q−1=q∗/∣∣q∣∣2,(qaqb)−1=(qb)−1(qa)−1 - 数乘与点乘 类似于向量的数乘和点乘/
2.1.5 相似/仿射/射影变换
- 相似变换
T S = [ s R t 0 T 1 ] T_{S}=\left[\begin{array}{ll} s \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{T} & 1 \end{array}\right] TS=[sR0Tt1] - 仿射变换
T A = [ A t 0 T 1 ] T_{A}=\left[\begin{array}{ll} A & \boldsymbol{t} \\ \mathbf{0}^{T} & 1 \end{array}\right] TA=[A0Tt1]
其中只要求A是一个可逆矩阵,而不是正交矩阵 - 射影变换
T P = [ A t a T 1 ] T_{P}=\left[\begin{array}{ll} A & \boldsymbol{t} \\ \mathbf{a}^{T} & 1 \end{array}\right] TP=[AaTt1]
可以对真个矩阵除以v得到一个右下角为1的矩阵,此时有15个自由度 - 从真实世界到相机照片的变换可以看成一个射影变化,如果相机的i焦距为无穷远,那么这个变换则为仿射变换
3.代码部分
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)