⭐️这篇博客要给大家介绍一个新的数据结构——位图。位图听上去就是和比特位相关联，它有什么作用呢，下面为大家介绍。
⭐️博客代码已上传至gitee：https://gitee.com/byte-binxin/cpp-class-code

---

🌏概念

位图： 所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

适用场景： 如果我们需要对大量的数据进行处理，判断该数据在不在，比如40亿个整形数据，如果我们用unordered_set来存放这些数据，大约需要占用16G的内存，显然这是不妥的，如果我们选择用一个数据结构，该数据结构可以存放40亿个数据在不在的状态，也就是开42亿个比特位大小的空间（整形数据总共是约42亿个），约500M，这样就可以将数据存下去了。

如下图： （其中1代表在，0代表不在，所以1，2，5，7这几个元素是在的）

🌏实现

🌲整体框架

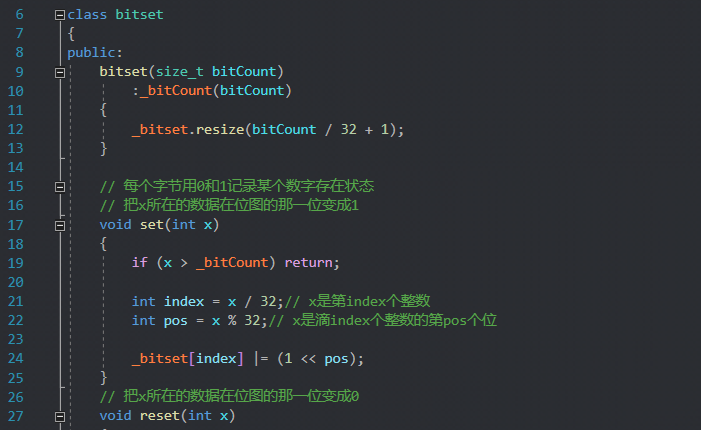
我们选择用一个vector来存放数据，还有一个成员变量就是代表开了多大比特位的空间。在构造函数中，根据用户传入的多大字节，代表可以记录0到_bitCount这些数的状态，其中我们把bitCount除以32再加1，判断多少个整形可以有这么多字节的空间，但是会浪费几个比特位，这些空间都是可以忽略的。

class bitset
{
public:
	bitset(size_t bitCount)
			:_bitCount(bitCount)
	{
		_bitset.resize(bitCount / 32 + 1);
	}
private:
	vector<int> _bitset;
	int _bitCount;// 开num比特位的空间
};

🌲把某一位设置为1

分为两步：

1. 找到x所处在的那一位： 先确定这个数应该处在第几个整数，也就是index=x/32;然后通过把x对32取模，得到x在第index个整形的第pos个位置
2. 把改为设置为1： 把1左右pos位，然后得到00…010…00，用这个数和第index整数进行按位或的操作

代码实现如下：

// 每个字节用0和1记录某个数字存在状态
// 把x所在的数据在位图的那一位变成1
void set(int x)
{
	if (x > _bitCount) return;

	int index = x / 32;// x是第index个整数
	int pos = x % 32;// x是滴index个整数的第pos个位

	_bitset[index] |= (1 << pos);
}

🌲把某一位设置为0

分为两步：

1. 找到那一位： 和上面的方法一样
2. 把这位设置为0： 把1左右pos位，然后得到00…010…00，把这个数取反，然后和第index个整数进行按位与的操作

代码实现如下：

// 把x所在的数据在位图的那一位变成0
void reset(int x)
{
	if (x > _bitCount) return;

	int index = x / 32;// x是第index个整数
	int pos = x % 32;// x是滴index个整数的第pos个位

	_bitset[index] &= ~(1 << pos);
}

🌲判断某一位是否为1

分为两步：

1. 找到那一位： 和上面的方法一样
2. 把这位设置为0： 把1左右pos位，然后得到00…010…00，然后返回这个数和第index个整数进行位与的的结果

代码实现如下：

// 判断x是否存在
bool test(int x)
{
	if (x > _bitCount) return false;

	int index = x / 32;// x是第index个整数
	int pos = x % 32;// x是滴index个整数的第pos个位

	return _bitset[index] & (1 << pos);
}

🌲测试

测试代码如下：

void TesstBitset1()
{
	bitset bs(100);

	bs.set(99);
	bs.set(0);
	bs.set(98);
	bs.set(55);
	bs.set(75);
	bs.set(35);

;
	bs.reset(99);
	bs.reset(87);

	for (size_t i = 0; i <= 100; ++i)
	{
		cout << i << ":" << bs.test(i) << " ";
		if (i != 0 && i % 10 == 0)
			cout << endl;
	}
}

代码运行结果如下：

🌏位图的应用

有以下几个：

1. 快速查找某个数据是否在一个集合中
2. 排序+去重
3. 操作系统中磁盘的标记等

缺点： 只能处理整形数据

🌐总结

位图实现起来十分的简单，但是应用也是很广的，节省空间，但是它有一个致命的缺点就是只能处理整形数据，下一篇博客会介绍一个可以处理其他类型的数据结构——布隆过滤器。今天就先介绍到这里，喜欢的话，欢迎点赞支持和关注~