-
1956年，在达特茅斯会议上，麦卡锡提议用AI作为这一交叉学科，标志着人工智能学科的诞生。麦卡锡也被称为人工智能之父。P3
-
1950年，阿兰﹒图灵提出了图灵测试，为智能提供一个满足可操作要求的定义。图灵测试用人类的表现来衡量假设的智能机器的表现。P3
-
人工智能的产生和发展经历了哪几个阶段？P5
孕育期、形成期(兴旺期)、萧条波折区、二次兴旺期、稳步增长期
20世纪50年代中期以前 孕育期
20世纪50年代中期至60年代中期 形成及第一个兴旺期
20世纪60年代中期至70年代中期 萧条波折期
20世纪70年代中期至80年代中期 第二个兴旺期
20世纪80年代中期至今 稳步增长期
-
人工智能研究有哪几个学派？其特点是什么？P12
符号主义学派：基于 物理符号系统假设 和 有限 合理性原理
连接主意学派：基于 神经网络 和 网络间的连接机制 与 学习算法
行为主义学派： 基于 控制论 和 “动作-感知”控制系统
符号主义学派：解决逻辑思维问题，难以模拟形象思维；信息转换后，信息有丢失的情况发生。
连接主义学派：不适合解决逻辑思维问题，不适合多种知识的开发。
行为主义学派：智能取决于感知和行动，智能行为只能在现实世界中，通过与周围环境的交互表现出来，人工智能可以像人类智能一样逐步进化，分阶段发展并增强。
-
人工智能是一门综合性交叉学科和边缘学科，列举至少六个研究领域(P17)
专家系统、模式识别、自然语言处理、智能决策支持系统、神经网络、自动定理证明、博弈、智能检索、机器视觉
-
人工智能常用知识表示方法包含了：
1.一阶谓词表示法
2.产生式表示法
3.语义网络表示法
4.框架表示
5.脚本表示法
6.面向对象表示法。
-
在逻辑系统中，最简单的逻辑系统就是命题。所谓命题，就是具有真假意义的陈述句。P27
-
产生式的基本形式？产生式与蕴涵式的区别？P34
P→Q (IF P THEN Q)
产生式的基本形式与逻辑谓词的蕴含式具有相同的形式.
蕴含式是产生式的一种特殊情况。
蕴含式:只能表示精确性知识，其逻辑值要么为真，要么为假
产生式:不仅可以表示精确性知识，还可以表示不精确知识。
- 产生式表示法的优点？缺点？P37
优点：清晰性、模块性、自然性
缺点：难以扩展、规则选择效率较低
- 设有下列语句，请用相应的谓词公式把它们表示出来。
(1) 有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。
解：
设：x表示某个人
Like(x,y) 表示x喜欢y
meihua：梅花
juhua：菊花
有的人喜欢梅花：∃(x)Like(x,meihua)
有的人喜欢菊花：∃(x)Like(x,juhua))
有的人既喜欢梅花又喜欢菊花：∃(x)(Like(x,meihua)∧Like(x,Jjuhua))(2) 重庆市的夏天既炎热又干燥。
解：
设：x表示某个城市
Summer(x):表示某个城市的夏天
Hot(x) 表示x炎热
Dry(x) 表示x干燥
重庆：chongqing
Hot(Summer(chongqing))∧Dry(Summer(chongqing))(3) 有一个人是所有学生的老师。
解：
设：x表示某个人
Student(x) 表示x是学生
Teach(x,y) 表示：x是y的老师
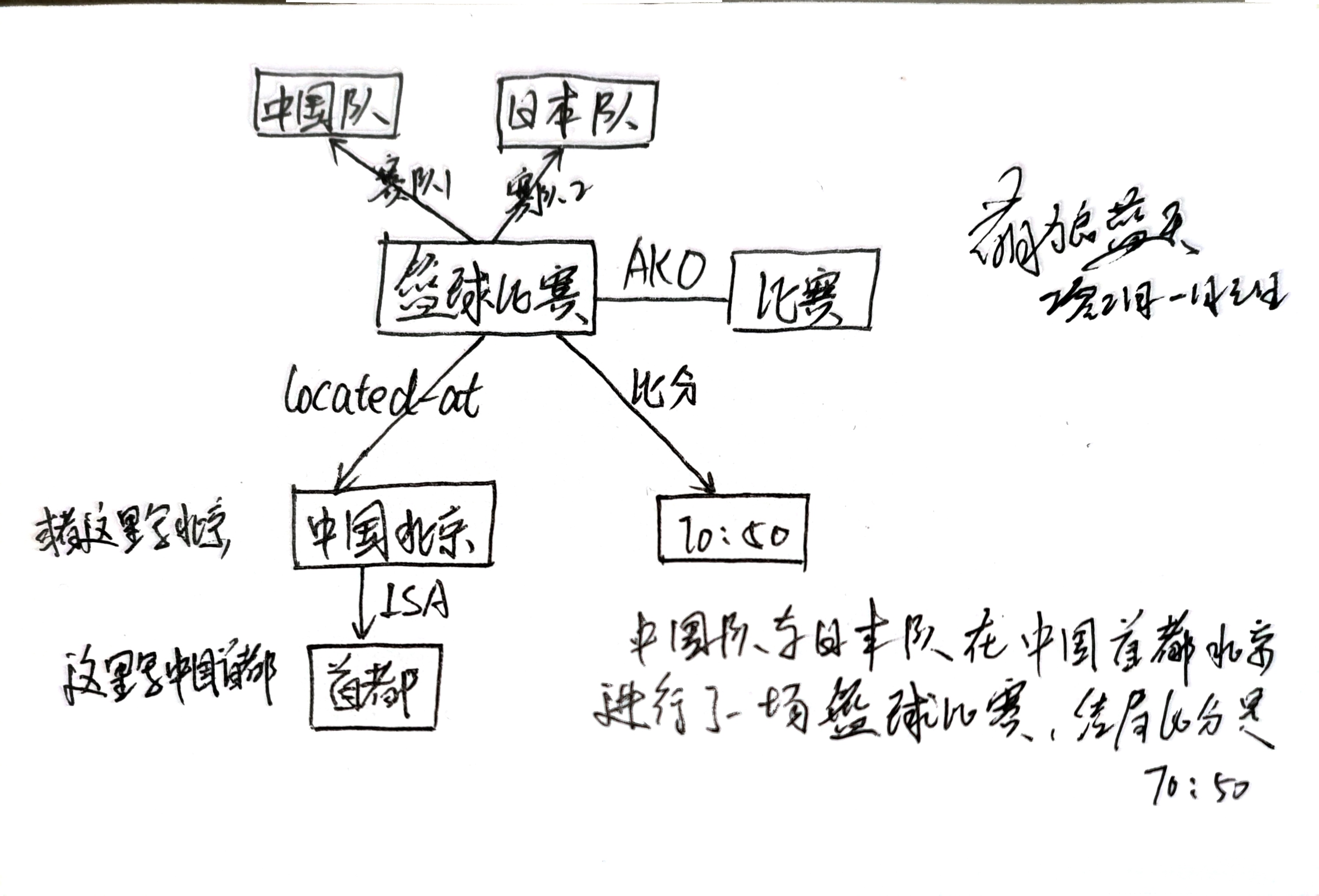
∃x(∀y(Student(y))--> Teach(x,y))- 请把下列语句用语义网络表示出来。
(1) 中国队与日本队在中国首都北京进行了一场篮球比赛，结局的比分是70:50.
(2) 王丽萍是天发电脑公司的经理，她35岁，住在南内环街68号。
-
框架的基本结构.P46
<框架名> 槽名n :侧面名n1 值n1 侧面名n2 值n2 …… 约束:约束条件n -
请把下列命题表示的事实用一个语义网络表示出来。
(1) 树和草都是植物。
(2) 树和草都是有根有叶的。
(3) 水草是草，且生长在水中。
(4) 果树是树，且有果实。
(5) 苹果树是一种果树，它有苹果。
- 请把下列命题表示的事实用一个语义网络表示出来.
(1) 猪和羊都是动物；
(2) 猪和羊都是哺乳动物；
(3) 野猪是猪，但生长在森林中；
(4) 山羊是羊，头上长着角；
(5) 绵羊是一种羊，它能生产羊毛。
- 假设有以下一段天气预报：“合川地区今天白天阴天，东南风4级，最高气温11℃，最低气温4℃，降水概率30%。”请用框架表示这一知识。
天气预报：
地区：合川
日期：今天
时间：白天
天气状况：阴天
风向：东南风
风力等级：4级
最高气温：11℃
最低气温：4℃
降水概率：30%-
推理的分类。
-
按照推理途径来分，推理可以分为：
- 演绎推理
- 归纳推理
- 默认推理。
-
按照推理过程中所使用的知识的确定性来分：
- 确定性推理
- 不确定性推理。
-
-
子句和子句集的概念。P69
-
文字：原子谓词公式及其否定
-
子句任何文字的析取式
-
空子句：不含任何文字的子句
-
子句集：由空子句构成的集合
-
-
判断下列公式是否为可合一，若可合一，则求出最一般合一MGU。
(1) 
考虑两个公式 (P(a, b)) 和 (P(x, y))。
- 初始化：开始时，合一映射(unifier)是空的，记作 (\varnothing)。
- 比较结构：两个公式的结构相同，都是形如 (P(_, _)) 的谓词表达式。其中第一个参数在第一个公式中是常量 (a)，在第二个公式中是变量 (x)；第二个参数在第一个公式中是常量 (b)，在第二个公式中是变量 (y)。
- 处理变量冲突：由于 (x) 和 (a) 在不同的公式中占据相同的位置，我们需要考虑它们是否可以合一。在这种情况下，我们可以将变量 (x) 映射到常量 (a)，即添加一个替换 ({x/a}) 到合一映射中。类似地，我们可以将变量 (y) 映射到常量 (b)，即添加 ({y/b}) 到合一映射中。
- 更新合一映射：将两个替换组合起来，得到合一映射 ({x/a, y/b})。
- 检查合一结果：在当前的合一映射下，(P(x, y)) 变为 (P(a, b))，与第一个公式完全一致。因此，两个公式是可合一的，并且它们的最一般合一(Most General Unifier, MGU)是 ({x/a, y/b})。
在这个例子中，没有发生任何冲突，因为每个变量都可以直接映射到一个常量上。这是最简单的合一情况之一。在实际应用中，合一问题可能会更加复杂，涉及更多的变量、常量、函数符号和嵌套结构。然而，基本的原则和步骤是类似的：比较结构、处理变量冲突、更新合一映射并检查结果。
解答：可合一 最一般合一为：{a/x，b/y}
(2) 
- 初始化：合一映射(unifier)开始时是空的，记作 (\varnothing)。
- 比较结构：两个公式的最外层结构相同，都是形如 (P(_, _)) 的谓词。其中第一个参数在第一个公式中是复合项 (f(x))，在第二个公式中是变量 (y)；第二个参数在第一个公式中是常量 (b)，在第二个公式中是变量 (z)。
- 处理变量和复合项：
- 对于第一个参数，我们有复合项 (f(x)) 和变量 (y)。由于 (y) 是变量，它可以被替换为任何项，包括 (f(x))。因此，我们可以将替换 ({y/f(x)}) 加入到合一映射中。
- 对于第二个参数，我们有常量 (b) 和变量 (z)。同样地，由于 (z) 是变量，它可以被替换为任何项，包括常量 (b)。因此，我们可以将替换 ({z/b}) 加入到合一映射中。
- 更新合一映射：将两个替换组合起来，得到合一映射 ({y/f(x), z/b})。
- 检查合一结果：在当前的合一映射下，(P(y, z)) 变为 (P(f(x), b))，与第一个公式完全一致。因此，两个公式是可合一的，并且它们的最一般合一(Most General Unifier, MGU)是 ({y/f(x), z/b})。
可合一 {y/f(x),z/b}(3) 
- 初始化：合一映射(unifier)开始时是空的，记作 (\varnothing)。
- 比较结构：两个公式的最外层结构相同，都是形如 (P(_, _, _)) 的谓词。我们需要比较这三个参数。
- 处理参数：
- 第一个参数：在第一个公式中是复合项 (f(y))，在第二个公式中是变量 (x)。由于 (x) 是变量，它可以被替换为任何项，包括 (f(y))。因此，我们可以考虑将替换 ({x/f(y)}) 加入到合一映射中(但注意，这个替换可能与后面的参数产生冲突，所以我们需要继续检查)。
- 第二个参数：在第一个公式中是变量 (y)，在第二个公式中是复合项 (f(a))。这里我们不能直接将 (y) 替换为 (f(a)) 或反之，因为这会导致第一个参数中的 (f(y)) 也被改变。我们需要找到一个更复杂的替换或者判断为不可合一。
- 第三个参数：在第一个公式中是变量 (x)，在第二个公式中是复合项 (f(b))。同样地，这里也不能直接将 (x) 替换为 (f(b))，因为这会导致第一个参数中的 (x)(如果前面的替换 ({x/f(y)}) 被应用的话)也被改变。
- 检查冲突：显然，如果我们尝试应用替换 ({x/f(y)}) 来解决第一个参数的冲突，那么这将会与第三个参数产生冲突，因为第三个参数中的 (x) 不能被替换为 (f(y))(否则就与第二个公式的 (f(b)) 不匹配了)。因此，这两个公式在当前的合一映射下是不可合一的。
- 结论：在当前的形式下，公式 (P(f(y), y, x)) 和 (P(x, f(a), f(b))) 是不可合一的。这是因为我们无法找到一个合适的替换来同时满足所有参数的合一条件。
{x/f(y),f(a)/y,f(b)/x}
Error - 不可合一(4) 
- 初始化：合一映射(unifier)开始时是空的，记作 (\varnothing)。
- 比较结构：两个公式的最外层结构相同，都是形如 (P(_, _)) 的谓词。我们需要比较这两个参数。
- 处理参数：
- 第一个参数：在第一个公式中是复合项 (f(x))，在第二个公式中是变量 (y)。由于 (y) 是变量，它可以被替换为任何项，包括 (f(x))。但我们不能立即做出这样的替换，因为还需要考虑第二个参数。
- 第二个参数：在第一个公式中是变量 (y)，在第二个公式中是复合项 (f(b))。这里我们也不能直接将 (y) 替换为 (f(b))，因为这会影响第一个公式中第一个参数的替换。
- 检查合一性：为了合一这两个公式，我们需要找到一个替换使得第一个公式的第一个参数能与第二个公式的第一个参数合一，并且第一个公式的第二个参数能与第二个公式的第二个参数合一。然而，在当前情况下，我们无法找到这样的替换，因为：
- 如果我们将 (y) 替换为 (f(x))(为了使第一个公式的第一个参数与第二个公式的第一个参数合一)，那么第一个公式的第二个参数也会变成 (f(x))，这显然无法与第二个公式的第二个参数 (f(b)) 合一，除非 (x) 和 (b) 是相同的(这在当前的上下文中并没有给出)。
- 如果我们尝试其他替换，比如将 (x) 替换为 (b)，那么第一个公式的第一个参数会变成 (f(b))，而第二个参数仍然是 (y)。这虽然使得第一个公式的第一个参数与第二个公式的第二个参数合一了，但第一个公式的第二个参数仍然没有与第二个公式的第一个参数合一。
- 结论：因此，在当前的形式下，公式 (P(f(x), y)) 和 (P(y, f(b))) 是不可合一的，因为我们无法找到一个合适的替换来同时满足所有参数的合一条件
{y/f(x),f(b)/y}
Error - 不可合一考虑两个公式 (P(f(x), y)) 和 (P(y, f(b)))。
- 结构比较：两个公式都有相同的谓词 (P)，但参数顺序不同。
- 合一尝试
- 第一个公式的第一个参数 (f(x)) 需要与第二个公式的第一个参数 (y) 合一。
- 第一个公式的第二个参数 (y) 需要与第二个公式的第二个参数 (f(b)) 合一。
然而，直接合一是不可能的，因为：
- 如果我们让 (y = f(x))，那么第一个公式的第二个参数就变成了 (f(x))，而第二个公式的第一个参数是 (y)，这样它们就相等了，但第二个公式的第二个参数是 (f(b))，它不等于 (f(x)) 除非 (x = b)，但这个信息并没有给出。
- 没有其他简单的替换可以同时解决这两个参数的合一问题。
- 结论：因此，这两个公式在当前形式下是不可合一的。
- 判断下列子句集中哪些是不可满足的。
(1) 
给定子句集 (S = {$\lnot $P \(\lor\) Q,$ \lnot$ Q, P, $\lnot $P})，我们可以使用归结推理(resolution)来判断其是否不可满足。归结推理是一种反证法，用于在命题逻辑和一阶逻辑中证明子句集的不可满足性。
首先，我们注意到子句集中直接包含了两个互补的文字：(P) 和 (\lnot P)。这意味着这两个子句本身就构成了一个矛盾，因为不可能同时为两个互补的文字赋予真值。
由于 (P) 和 ($\lnot $P) 已经在子句集中出现，我们可以立即得出结论：该子句集是不可满足的，因为它包含了显式的矛盾。
如果我们想要通过归结推理的形式化步骤来展示这一点，可以这样做：
Step1:从子句 ($\lnot $P $\lor $Q) 和 (P) 中，我们可以归结出 (Q)。
Step2:然后，从归结出的 (Q) 和子句 ($\lnot $Q) 中，我们可以归结出空子句(⊥)。
(2) 
$ (S = {P \lor Q, \lnot P \lor Q, P \lor \lnot Q, \lnot P \lor \lnot Q}) $是不可满足的。
观察子句：首先，我们观察子句集 (S)。它包含了四个子句，每个子句都是两个文字的析取(即“或”关系)。
核心思路：要判断一个子句集是否不可满足，我们需要考虑是否有可能为所有命题变量(在这里是 (P) 和 (Q))分配真值(真或假)，使得所有子句都为假。如果不可能，那么子句集就是不可满足的。
分析：
- 如果 (P) 为真且 (Q) 为真，那么第一个子句 (P \lor Q) 为真。
- 如果 (P) 为假且 (Q) 为真，那么第二个子句 (\lnot P \lor Q) 为真。
- 如果 (P) 为真且 (Q) 为假，那么第三个子句 (P \lor \lnot Q) 为真。
- 如果 (P) 为假且 (Q) 也为假，那么第四个子句 (\lnot P \lor \lnot Q) 为真。
无论我们如何为 (P) 和 (Q) 分配真值，总会有至少一个子句被满足(即为真)。因此，不存在一种真值分配方式使得所有子句都为假。
结论：由于不存在一种真值分配方式使得所有子句都为假，我们可以得出结论：子句集 (S) 是不可满足的。
(3) 
没有关于函数 (f)、变量 (x)、(y)、和 (a) 的具体信息，以及命题函数 (P)、(Q) 和 (R) 的具体解释，我们不能确定子句集 (S) 是否不可满足
(4) 
\((S = \{P(x) \lor Q(x) \lor R(x), \lnot P(y) \lor R(y), \lnot Q(a), \lnot R(b)\})\)
条件不足，无法判定为是不可满足的
- 把下列谓词公式分别化为相应的子句集。
(1) 
∀x ∀y (P(x, y) → Q(x, y))
{ ¬P(x, y) ∨ Q(x, y) }(2) 
\((\forall x)(\exists y)(P(x, y) \lor Q(x, y) \rightarrow R(x, y))\)
(3) 
为了将其转换为子句集形式或一种更便于处理的形式，我们需要逐步进行转换：
消除蕴含符号
：首先处理内部的蕴含符号，然后再处理外部的。
- 对于 Q(x,y)→R(x,y)，转换为 ¬Q(x,y)∨R(x,y)。
- 对于 (∀y)P(x,y)→¬(∀y)(¬Q(x,y)∨R(x,y))，转换为 ¬(∀y)P(x,y)∨¬(∀y)(¬Q(x,y)∨R(x,y))。
处理否定的全称量词：将否定的全称量词转换为存在量词。
- ¬(∀y)P(x,y) 转换为 (∃y)¬P(x,y)。
- ¬(∀y)(¬Q(x,y)∨R(x,y)) 转换为 (∃y)¬(¬Q(x,y)∨R(x,y))，进一步应用德摩根定律得到 (∃y)(Q(x,y)∧¬R(x,y))。
合并结果：将上述转换合并回原公式。
- 最终得到：(∀x)[(∃y)¬P(x,y)∨(∃y)(Q(x,y)∧¬R(x,y))]。
(4) 
- 已知：
求证G是F的逻辑结论。P75
-
根据在问题求解问题过程中是否运用启发性知识，搜索分为：盲目搜索和启发式搜索。
其中，典型的盲目搜索有深度优先搜索和宽度优先搜索。P86
-
常见四种搜索策略的比较。P99
深度优先
广度优先
最佳优先
A*
-
写出图中树的结点的访问序列，要求满足以下两个搜索策略。
(1) 深度优先搜索
1-2-5-6-10-11-3-7-12-13-4-8-9(2) 宽度优先搜索(也叫广度优先搜索)
1-2-3-4-5-6-7-8-9-10-11-12-13
- A算法与AO算法的比较。P117
A*算法：结合了最佳优先搜索和广度优先搜索的特性，使用启发式函数评估节点，寻找最优解。
AO*算法：先建立搜索图，然后通过跟踪有标记的连接符，计算局部解图，再选择非终叶节点进行扩展，并计算后继节点的费用
- 对于八数码难题按下式定义估价函数：
其中
为节点
的深度; 
是所有棋子偏离目标位置的曼哈顿距离(棋子偏离目标位置的水平距离和垂直距离和)，例如下图所示的初始状态
中棋子8的曼哈顿距离为2;棋子2的曼哈顿距离为1;棋子1的曼哈顿距离为1;棋子6的曼哈顿距离为1; 
。
|
| |
| 初始状态 |
| 目标状态 |
用A*搜索法搜索目标，并给出各个搜索循环结束时OPEN和CLOSE表的内容。
- 简述问题规约求解问题的实质。
- 设有如图所示的与/或树，请分别按和代价法及最大代价法求解树的代价。
- 设有如下图所示的博弈树，其中最下面的数字是假设的估值，请对该博弈树作如下工作：
(1) 计算各节点的倒推值；
(2) 利用α-β剪枝技术剪去不必要的分枝。
- 主观贝叶斯方法中，规则的不确定性可表示为：
其中，(LS,LN)表示规则强度，LS和LN分别表示充分性度量和必要性度量。
- 证据不确定性的表示，在CF模型中，证据E的不确定性也是可以用可信度因子CF(E)来表示，其取值范围同样是
，其典型值为：
当证据E肯定为真时，
当证据E肯定为假时，
当证据E一无所知时，
-
试证明：对
的信任增长度等于
的不信任增长度。P142 -
CF中的不确定性推理实际上是从不确定性的初始证据出发，不断运用相关的不确定性规则，逐步推出最终结论和该结论的可信度的过程。P143
-
在证据理论中可以分别用信任函数、似然函数以及类概率函数来描述知识的精确信任度、不可驳斥信任度以及估计信任度，即可以从不同的角度刻画命题的不确定性。P147
-
设有三个独立的结论H1、H2、H3及两个独立的证据E1、E2，它们的先验概率和条件概率分别为：
(1) 当只有证据
出现时，
以及
的值，并说明
\(E_1\)的出现对
的影响。
(2) 当\(E_1\)和
同时出现时，
及
的值，并说明\(E_1\)和
\(E_2\)同时出现时对
的影响。
- 设有如下知识：
求：当证据
分别存在和不存在时，
和
的值各是多少？
- 设有如下知识：
求：当证据
分别存在和不存在时，
和
的值各是多少？
- 设有如下规则：
且已知：
，求H的综合可信度CF(H)。
- 设有如下规则：
且已知：
，求H的综合可信度CF(H)。
- 设
，且从不同知识源得到的概率分配函数分别为：
求正交和
。
- 设
，有如下计算概率分配函数
设
，求
、
和
的值。
- 机器学习的分类。P168
(1) 基于学习方式的分类。
(2) 基于学习目标的分类。
-
归纳学习是指个别到一般、从部分到整体的一类推论行为。
归纳推理是应用归纳方法所进行的推理，即从足够多的事例中归纳出一般性的知识，是一种从个别到一般的推理。P169
-
专家系统的结构，一般情况下，专家系统的基本结构由知识库、综合数据库、推理机、解释器、知识获取模块和人机交互界面六部分组成。P210
已为社区贡献4条内容
所有评论(0)