Tarjan 算法（超详细！！）

之前太多错误了，重构了

一棵油菜花

3238人浏览 · 2024-01-24 22:19:15

一棵油菜花 · 2024-01-24 22:19:15 发布

推荐在 cnblogs 上阅读

Tarjan 算法

前言

说来惭愧，这个模板仅是绿的算法至今我才学会。

我还记得去年 CSP2023 坐大巴路上拿着书背 Tarjan 的模板（CSP2024 也没学会）。虽然那年没有考连通分量类似的题目（2024 也没有）。

现在做题遇到了 Tarjan，那么，重学，开写！

另，要想学好此算法的第一件事——膜拜 Tarjan 爷爷。

再序（upd on 2024.11.4）

这个东西意外成为了我博客下最多人收藏的文章，我在 CSP2024 前重新复习时发现仍然漏洞百出，为了对大家负责我决定重构整篇。

顺带补上边双和点双。

定义

强连通分量

一个图的子图若任意两点之间均有路径可达，则成该子图为原图的强连通分量。

割点

如果一个连通分量内有一个点，把这个点及其邻边删掉后连通分量不再连通而变成了两个连通分量，那么这个点就是割点。下图中点 $2$ 就是割点。

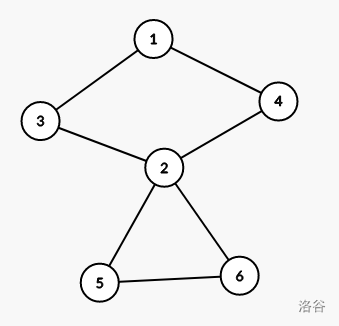
割边（桥）

与割点定义类似，删除某一边后连通分量不再连通。如下图 $(2, 5)$ 和 $(5, 6)$ 都是割边。

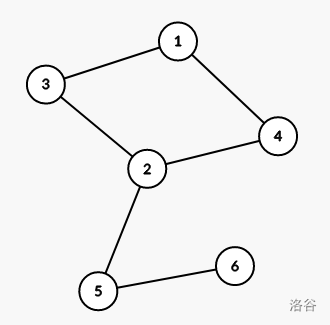
点双连通分量

定义：没有割点的双连通分量。“双连通分量”指任意两点都有两条不同路径可达。

边双连通分量

定义：没有割边的双连通分量。

如何求割点

采用 Tarjan 求割点。思想：在 dfs 时访问到 $k$ 点时，图会被点 $k$ 分为已访问和未访问两部分。如果 $k$ 是割点，那么一定存在没有访问过的点在不经过 $k$ 的情况下不能访问到已访问过的点。

这里要用到回溯值 low[u] 表示点 $u$ 可以访问到时间戳（dfn[u]=++tim）最小的节点。

根据这些信息来判断割点：

若当前点是根节点，如果子树数量大于 $1$ 则说明该点为割点。
若当前点不是根节点，如果存在一个儿子的回溯值大于等于该点的时间戳（low[v]>=dfn[u]），则该点为割点（因为儿子无法绕过该点去访问时间戳更小的点）。

如何求割边

判断割边的条件是一条边 $(u, v)$ 有 low[v]>dfn[u]。如果相等意味着点 $v$ 还可以回到点 $u$ ，所以不相等意味着连父亲也回不到。如果点 $v$ 回不到祖先，也无法绕过 $(u, v)$ 这条边回到父亲，那么 $(u, v)$ 就是割边。

如何求点双

点双模板题。

点双是没有割点的双连通分量，一个割点可能属于多个点双，非割点只属于一个点双。那么我们可以在 dfs 的过程中压点入栈，判断到当前点为割点时，就不断弹栈，弹出来的节点都属于一个点双。

注意特判一个点就是一个子图的情况也是点双。

#include<bits/stdc++.h>
using namespace std;

#define int long long

const int N=2e6+5;

int n,m;
int dfn[N],low[N],tim,cnt;
vector<int> G[N],ans[N];
int stk[N],top;

void tarjan(int u,int pa)
{
    dfn[u]=low[u]=++tim;
    stk[++top]=u;
    int son=0;
    for(int v:G[u]){
        if(!dfn[v]){
            tarjan(v,u);
            ++son;
            low[u]=min(low[u],low[v]);
            if(pa==0&&son>1||low[v]>=dfn[u]){
                ++cnt;
                while(stk[top+1]!=v)
                    ans[cnt].push_back(stk[top--]);
                ans[cnt].push_back(u);
            }
        }else if(v!=pa)
            low[u]=min(low[u],dfn[v]);
    }
    if(pa==0&&son==0)
        ans[++cnt].push_back(u);
}

signed main()
{
    scanf("%lld%lld",&n,&m);
    for(int i=1,u,v;i<=m;i++){
        scanf("%lld%lld",&u,&v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i]){
            top=0;
            tarjan(i,0);
        }
    }
    printf("%lld\n",cnt);
    for(int i=1;i<=cnt;i++){
        printf("%lld ",ans[i].size());
        for(int j:ans[i])
            printf("%lld ",j);
        puts("");
    }
    return 0;
}

如何求边双

边双模板题

判断割边的实现可以放在枚举儿子的循环外面，此时判断点 $u$ 与其父亲的边是否是割边的条件等价为 low[u]==dfn[u]，代表点 $u$ 访问祖先的能力差到连父亲也访问不到了。这样方便我们找边双。

注意此题有向图，我们建双向边来处理，若访问到父亲则不再访问。但是题目有重边，即原本就有一条访问父亲的边，我们这样判断相当于删去了这次机会，所以我们改为不能访问上一条来的边。

#include<bits/stdc++.h>
using namespace std;

#define int long long

const int N=2e6+5;

int n,m;
int dfn[N],low[N],tim,cnt;
vector<pair<int,int>> G[N];
vector<int> ans[N];
int stk[N],top;
bool vis[N];

void tarjan(int u,int lst)
{
    dfn[u]=low[u]=++tim;
    stk[++top]=u;
    int son=0;
    for(auto [v,i]:G[u]){
        if(i==(lst^1))
            continue;
        if(!dfn[v]){
            tarjan(v,i);
            low[u]=min(low[u],low[v]);
        }else
            low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]){
        ++cnt;
        ans[cnt].push_back(u);
        while(stk[top]!=u){
            ans[cnt].push_back(stk[top]);
            top--;
        }
        top--;
    }
}

signed main()
{
    scanf("%lld%lld",&n,&m);
    for(int i=1,u,v;i<=m;i++){
        scanf("%lld%lld",&u,&v);
        G[u].push_back({v,i*2});
        G[v].push_back({u,i*2+1});
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i]){
            top=0;
            tarjan(i,0);
        }
    }
    printf("%lld\n",cnt);
    for(int i=1;i<=cnt;i++){
        printf("%lld ",ans[i].size());
        for(int j:ans[i])
            printf("%lld ",j);
        puts("");
    }
    return 0;
}

如何求强连通分量

一个点只会属于一个强连通分量。强连通分量是极大的，意味着如果还能拓展更多节点，那么拓展后才是强连通分量。

还是搬上经典老图：

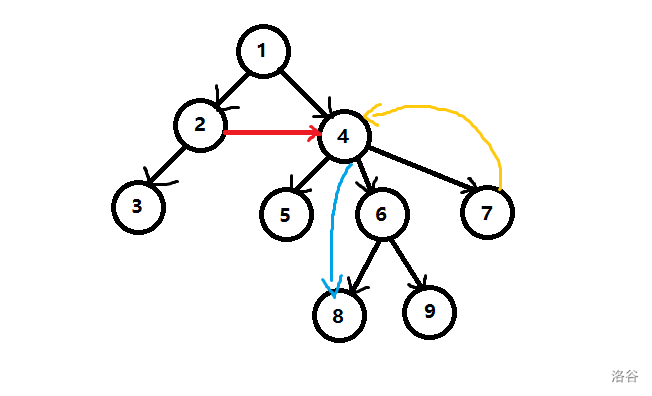
一张图中搜索出来一棵搜索树后，黑色的边是搜索走过的边，还有原图没走到的边，分三种：

横叉边（红）
前向边（蓝）
后向边（黄）

回溯值 low[u] 的转移除了从儿子的 low[v] 转移过来，如果遇到后向边，还可以从边指向的祖先的 dfn[v] 转移过来。

若 low[u]==dfn[u]，意味着当前点连父亲也无法访问，也意味着该点子树内所有还在栈中的点都和该点属于同一个强连通分量。

为什么要求在栈中而不是访问过呢？因为我们要避免走到横叉边。

强连通分量模板题

注意此题输出最大的强连通分量且按序输出。

#include <bits/stdc++.h>
using namespace std;

#define int long long

const int N=5e5+5;

int n,m;
vector<int> G[N];
int stk[N],top;
bool vis[N];
int cnt,dfn[N],low[N],tim;
vector<int> ans[N];
struct node
{
    int id,sz,num;
}p[N];

void tarjan(int u)
{
    low[u]=dfn[u]=++tim;
    stk[++top]=u;
    vis[u]=1;
    for(int v:G[u]){
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(vis[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u]){
        ++cnt;
        p[cnt].id=cnt;
        p[cnt].sz=1;
        p[cnt].num=u;
        ans[cnt].push_back(u);
        while(stk[top]!=u){
            p[cnt].sz++;
            p[cnt].num=min(p[cnt].num,stk[top]);
            ans[cnt].push_back(stk[top]);
            vis[stk[top]]=0;
            top--;
        }
        vis[u]=0;
        top--;
    }
}

signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1,u,v,op;i<=m;i++){
        cin>>u>>v>>op;
        if(op==1)
            G[u].push_back(v);
        else{
            G[u].push_back(v);
            G[v].push_back(u);
        }
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i]){
            top=0;
            tarjan(i);
        }
    sort(p+1,p+cnt+1,[](node x,node y){
        if(x.sz!=y.sz)
            return x.sz>y.sz;
        return x.num<y.num;
    });
    cout<<ans[p[1].id].size()<<'\n';
    sort(ans[p[1].id].begin(),ans[p[1].id].end());
    for(int i:ans[p[1].id])
        cout<<i<<' ';
    return 0;
}

强连通分量模板题 2

一样的，只有有向边了，更板。

#include <bits/stdc++.h>
using namespace std;

#define int long long

const int N=5e5+5;

int n,m;
vector<int> G[N];
int stk[N],top;
bool vis[N];
int cnt,dfn[N],low[N],tim;
vector<int> ans[N];
struct node
{
    int id,num;
}p[N];

void tarjan(int u)
{
    low[u]=dfn[u]=++tim;
    stk[++top]=u;
    vis[u]=1;
    for(int v:G[u]){
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }else if(vis[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u]){
        ++cnt;
        p[cnt].id=cnt;
        p[cnt].num=u;
        ans[cnt].push_back(u);
        while(stk[top]!=u){
            p[cnt].num=min(p[cnt].num,stk[top]);
            ans[cnt].push_back(stk[top]);
            vis[stk[top]]=0;
            top--;
        }
        vis[u]=0;
        top--;
    }
}

signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++){
        cin>>u>>v;
        G[u].push_back(v);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i]){
            top=0;
            tarjan(i);
        }
    sort(p+1,p+cnt+1,[](node x,node y){
        return x.num<y.num;
    });
    for(int i=1;i<=cnt;i++)
        sort(ans[i].begin(),ans[i].end());
    cout<<cnt<<'\n';
    for(int i=1;i<=cnt;i++){
        for(int j:ans[p[i].id])
            cout<<j<<' ';
        cout<<'\n';
    }
    return 0;
}

参考文献

开放原子开发者工作坊

开放原子开发者工作坊旨在鼓励更多人参与开源活动，与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动，如meetup、训练营等，主打技术交流，干货满满，真诚地邀请各位开发者共同参与！

更多推荐

一文解决Cellphonedb单细胞互作分析及可视化作图（2）

开放原子开发者工作坊

[工具使用]——时序图与UML类图

开放原子开发者工作坊

CTFHub技能树 Web-SQL注入详解

整数型注入我们输入 1不断尝试发现闭合方式就是 1 ，整数型存在两列order by 2存在两个注入点/?id=-1 union select 8,9爆库，当前数据库为sqli/?id=-1 union select 8,database()爆出所有表名,这里我们需要吧sqli转换为16进制/?id=-1 union select 8,group_concat(table_name) from i