一.前言

我在之前的文章中带大家学习了DFS，BFS算法。我提到过，用BFS算法求最短路径存在一些局限性—》

图论的基本算法是BFS和DFS，大多数图论高级算法都是从BFS和DFS发展出来的。从本篇文章开始，我们将一起学习数据结构——图的有关知识，并掌握更高阶的最短路径算法。

二.图的基础概念

👉在线性表中，数据元素是一对一的关系，如链表，如同手牵手一样，除了首元素后尾元素，中间的元素都有自己唯一的前驱和后驱。而在树形结构中，数据元素是一对多的关系，一个结点都有唯一的父结点，而可以有多个孩子。

👥对于图来说，则是多对多的关系。任何两个元素都可能有关系，每个节点可以有多个前驱和后继，但也有可能都没有。

图这种抽象模型由点（vertex）和连接点的边（edge）构成，为一个网状结构。

三.有向图和无向图理论基础

1.有向图

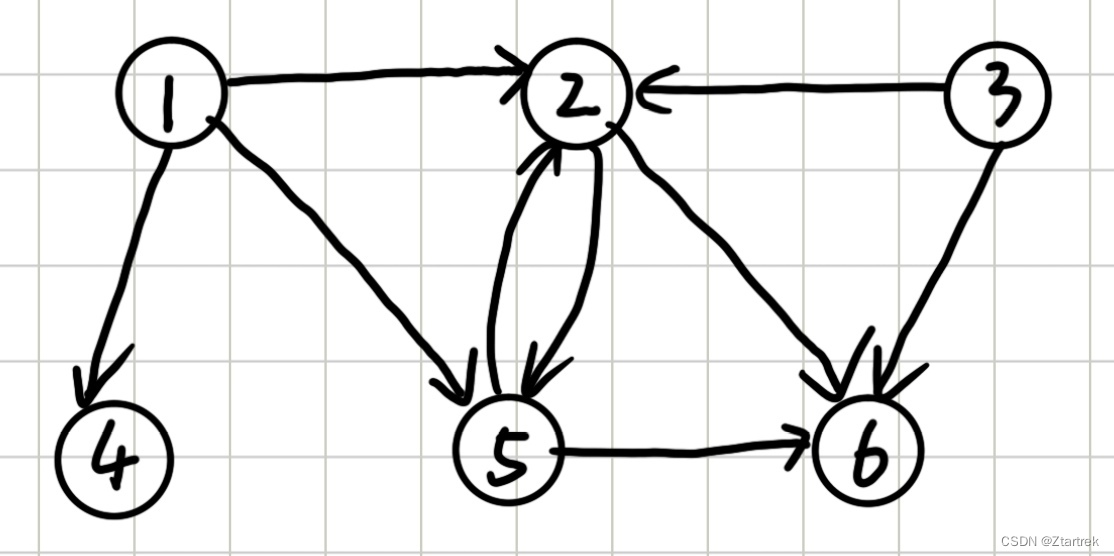
有向图，简写为digraph（即directgraph)，是由一个有限的称为顶点的元素集合以及一个有限的连接每对顶点的有向弧或有向边的集合构成的。如图所示：

如：节点2可以到5，6，节点135也都可到2（但2到不了1，3）。

⭐️对于以上图，节点一二间，箭头从1出发指向2，那么这条边对1来说是出向边，对节点二来说为入向边。 同时，一个节点也可以自己指向自己，那么这条边既是入向边又是出向边。

2.无向图 

1.边没有出向边和入向边之分。即两个节点间如果有边连接，则1可以到2，2可以到1。

2.顶点没有到达自己顶点位置的边。

3.顶点的度

有向图：分为顶点的出度，顶点的入度。

出度：即从这个顶点出去的边有几条。对上图的节点1，它的出度就是3.

入度：到达该节点的边有几条。对于上图的节点5，它的入度就是2.。

无向图：顶点的度。

即该顶点关联的边有几条。

四.图的表示方式：邻接矩阵

1.知识讲解

✨将有向图中所有的顶点编号为1，2......n，邻接矩阵是一个n×n的矩阵，如果节点j邻接于节点i（即有一条有向边直接从节点i指向节点j），那么矩阵第i行第j列的元素就为1，否则这个元素的值为0。

矩阵中，每一行代表一个元素，同一行的各列代表第i个元素是否指向第j个元素。

对于上面那幅图，顶点1指向2，4，5。则第一行的2，4，5列的元素为1，其余为0。同理，我们可以得出以下的矩阵图。

对于每一行，1的个数就表示出度。同时，对于每一列，1的个数就表示入度。 

👏注意：对于带权的有向图（可理解为每两个顶点之间的距离不一样），在邻接矩阵表示的时候，顶点i到顶点j的1就被“权值”所替换（只要不为0即可）。

有读者可能会有疑惑，邻接矩阵只能用来表示有向图吗？

它也可以用来表示无向图。如果i元素和j元素之间有边，则第i行第j列和第j行第i列的元素都要标注为1。

😎无向图的邻接矩阵特点：

1.对角线上全部是0。（因为顶点没有到达自己顶点位置的边）

2.以对角线为轴，左下和右上的存储完全是对称的。

局限性：

对于有向图的邻接矩阵来说，如果邻接矩阵是一个稀疏矩阵的话（可简单理解为点很多但边很少），存储的效率太低（空间利用率很低）。

而对于无向图，对角线都为0，而数据又对称，那存一半不就行了，所以空间利用率也低。

2.代码实现

邻接矩阵的代码实现其实很简单，用一个二维数组即可解决。我们一起来看看模板题。

输入：第一行共有两个整数，n和k，n代表有n个顶点，k代表有k条边。接下来的2~k+1行，每一行共有2个整数x,y，分别代表x和y相连（不为0）无向图！第k+2行输入一个t。

输出：第一行输出与顶点t直接相连的顶点的个数和所有的邻接点。

样例：

输入：5 3
          1 3
          2 4
          3 5
输出：3
           2
           1
           5

#include <iostream>
using namespace std;
int arr[100][100];

int main()
{
	int n, k;
	cin >> n >> k;
	for (int i = 1; i <= k; i++)
	{
		int x, y;
		cin >> x >> y;
		arr[x][y] = 1;
		arr[y][x] = 1;//二维数组存数据
	}
	int t;
	int cnt=0;
	cin >> t;
	for (int i = 1; i <= n; i++)
	{
		if (arr[t][i] == 1)
		{
			cnt++;
		}
	}
	cout << cnt << endl;
	for (int i = 1; i <=n; i++)
	{
		if (arr[t][i] == 1)
		{
			cout << i << endl;
		}
	}


	return 0;
}

代码很简单，对照我刚刚的讲解很容易理解。我们再来看看加权版本的。

 输入：第一行共有两个整数，n和k，n代表有n个顶点，k代表有k条边。接下来的2~k+1行，每一行共有3个整数x,y,z，分别代表x和y相连（不为0）无向图，并且权重为z。第k+2行输入一个t。

输出：前n行输出邻接矩阵的信息（邻接表中数字代表权重，若不连接权值为0）、

第n+1行输出与顶点t直接相连的顶点的个数和所有的邻接点。

样例：

输入

输入：5 3
          1 3 9
          2 4 5
          3 5 3

          3
输出：

0 0 9 0 0
0 0 0 5 0
9 0 0 0 3
0 5 0 0 0
0 0 3 0 0
2
1
5

#include <iostream>
using namespace std;

int arr[100][100];
int main()
{
	int n, k;
	cin >> n >> k;
	for (int i = 1; i <= k; i++)
	{
		int x, y,z;
		cin >> x >> y >> z;
		arr[x][y] = z;
		arr[y][x] = z;
	}
	int t;
	int cnt=0;
	cin >> t;
	for (int i = 1; i <=n; i++)
	{
		for (int j = 1; j <= n; j++)
		{

			cout << arr[i][j] << " ";
		}
		cout << endl;
	}
	for (int i = 1; i <= n; i++)
	{
		if (arr[t][i] >= 1)//注意if条件要改变
		{
			cnt++;
		}
	}
	cout << cnt << endl;
	for (int i = 1; i <=n; i++)
	{
		if (arr[t][i] >= 1)
		{
			cout << i << endl;
		}
	}


	return 0;
}

五.图的表示方式：邻接表 

 1.知识讲解

😳将有向图表示为一个数组或向量v[1],v[2],v[3]......，v[n]，每个元素对应有向图的一个节点，每个v[i]存储顶点i中的数据，以及一个包含所有邻接于顶点i的顶点编号的链表。

再把最初的地图放过来

它的邻接表就表示为：

🚀顶点表的各个结点由data和firstedge两个域表示，data是数据域，存储顶点的信息，fitstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。

在代码实现中，对于顶点我们可以这样写：

struct vertex

{

    string data;

    list<type>adjList;//即C++提供给我们的链表

}

而对于连接着的节点，我们这样实现

struct node

{

    int vex;//邻接的顶点

    int weight;//权重

} 

到时候我们把type换成struct node即可

 ❗️在邻接表中，我们只关心一个顶点邻接了哪些节点，我们不关心没邻接哪些点，所以这提高了空间利用率，这是相对于邻接矩阵的优点。但是，如果给出一个指定顶点，我们好像只能看到这个顶点可以到哪些顶点，即我们可以知道出度，但是我们看不到有哪些点可以到这个指定的顶点，即我们不知道入度。我们需要遍历整个邻接表，我们才能知道顶点的入度，这个效率确实低了。由此，有另一个东西，叫逆邻接表，来描述顶点的入度。

在这里，给出邻接表另一个模板（用数组实现链表，常用于竞赛中，提高程序效率）

🌸注意add插入数据的位置，是插在链表头部而不是尾巴。顺便提一下链表中插入数据的方式，以下图为例，我们需要将头节点和其连接的结点1断开，然后让结点3连接头节点与结点1。

int h[N];//头节点，存连接的节点的编号。因为是图不是单链表，图是多对多的关系，所以有多个“头”
int e[N * 2];//存放某节点的值
int ne[N * 2];//存放连接的下一节点的编号 
int idx=0;//编号
bool st[N];//状态数组（与dfs相关）

//邻接表用链表实现
void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

2.例题：树的重心

我们先来看题 ---》

 ①我们先理解一下题意，我将题目给的输入样例画了出来

 比如对于结点6，它便连接着三个连通块。每个连通块包含的结点数为4，1，3，那么删除结点6后，剩余各个连通块中点数的最大值便为4。同理，对于结点1可以得出它的最大值为7......将所有结点连接的连通块的最大结点数算出来后，从出选出最小值，便是最终答案。

 ②如何计算一个结点的最大连通块结点数？

我们首先分析一下结点6连通块的组成

我们可以发现分为结点6的上部分和结点6的子树的结点数。

那么我们可以分别计算。定义一个变量size=0，存结点6的最大子树的结点数（可以通过dfs向下搜索，回溯时返回子树的结点数），再定义一个变量sum=1，存放结点6及其子树的结点总数（包括结点6），最后用总结点数-sum，就可以得出结点6上部分的结点数。

定义一个变量answer

ans = min(ans, max(size, n - sum));

对于一个结点，先取其size和总数-sum的最大值，再将该最大值与其他已经得出的最大值比较，取最小值，程序最后遍历完后便能得出答案。

③如何存储树

树其实就是特殊的图，我们使用邻接表存储即可。 

 3.完整代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010; int ans = N;
int n=0;
int h[N];//头节点，存连接的节点的编号
int e[N * 2];//存放某节点的值
int ne[N * 2];//存放连接的下一节点的编号 
int idx=0;//编号
bool st[N];//状态数组

//邻接表用链表实现
void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}

int dfs(int u)
{
	st[u] = true;//标记为已经搜过了，防止向上搜
	int size = 0;//记录u的最大子树的结点数
	int sum = 1;//包含该节点及其所有子节点数
	for (int i = h[u]; i!=-1 ; i=ne[i])//i是节点的编号
	{
		int j = e[i];
		if (st[j])//防止重复搜索
		{
			continue;
		}
		int s = dfs(j);
		size = max(size, s);
		sum = sum += s;
	}
	ans = min(ans, max(size, n - sum));
	return sum;
}

int main()
{
	memset(h, -1, sizeof(h));
	scanf("%d", &n);
	for (int i = 1; i <n; i++)
	{
		int a, b;
		scanf("%d %d", &a, &b);
		add(a, b);
		add(b, a);//无向图加两次
	}
	dfs(1);//任取一个点开始深搜
	printf("%d\n", ans);
	return 0;
}

六.拓展知识 

如果用邻接表存储无向图，其实也可以，如果顶点1后面跟着顶点2，那么顶点2后面也会跟着顶点1，这也存在一个对称性。那么跟邻接矩阵其实一样了，都存在一个冗余存储的情况。而针对无向图有一个更好存储方式——邻接多重表。

对于有向图，如果我们想更方便的获取它的入度和出度，那么我们需要另一种表示方式——十字链表。

先给自己挖个坑，有关图的更多存储方式及图有关算法，我会在接下来的文章继续剖析。你的点赞关注收藏就是对我的最大支持！若有任何疑问欢迎在评论区留言，我们下篇文章再见~