HDR视频的传递函数

视频用传递函数Gamma、HLG、PQ压缩亮度，然而大多数开发对传递函数的参数不了解导致使用时出现问题，本篇文章讲的就是Gamma、HLG、PQ公式的各种参数详细解释。如果你觉得有所收获，来给HDR转SDR开源代码点个赞吧，你的鼓励是我前进最大的动力。

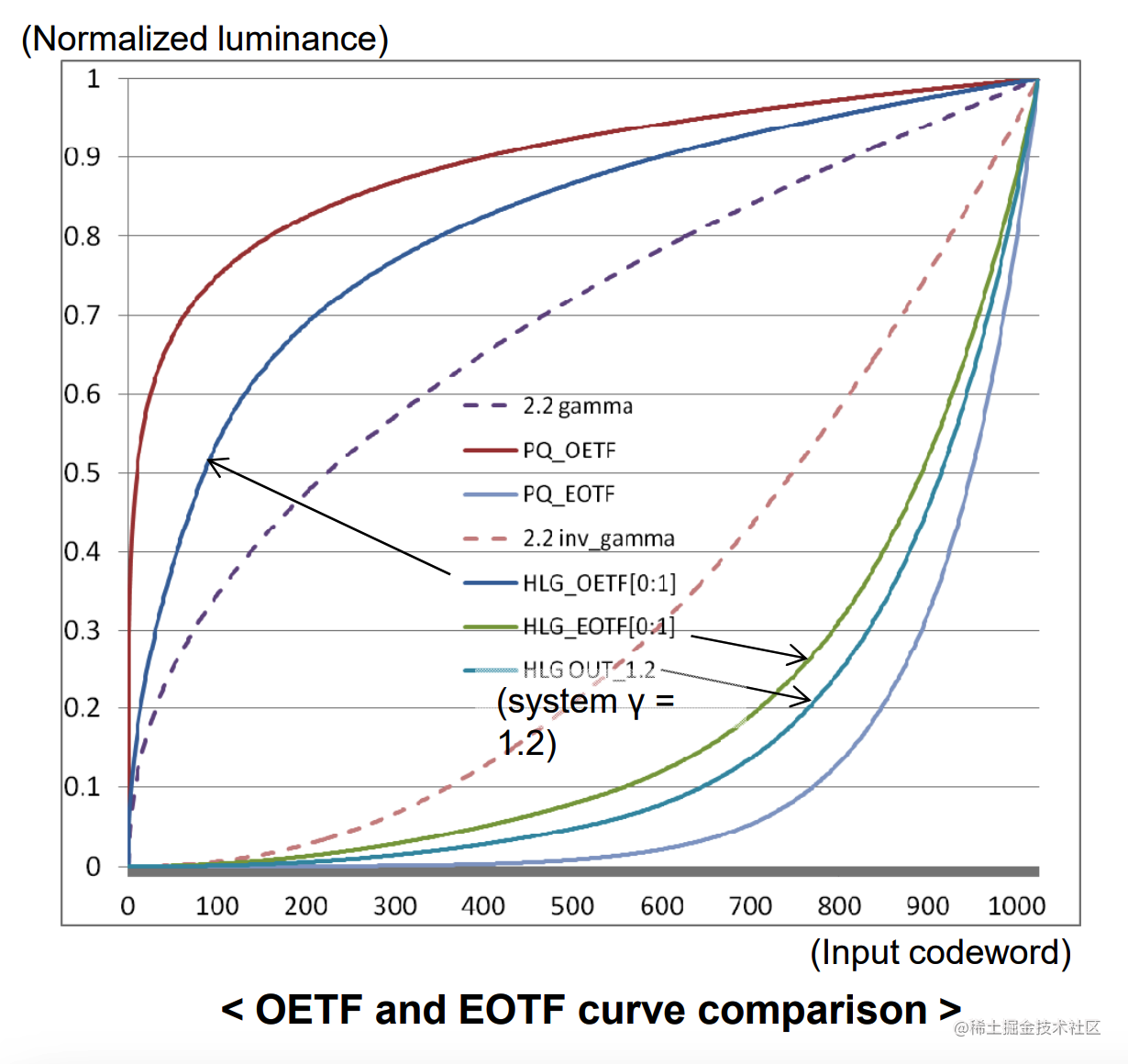
SDR视频的传递函数使用Gamma函数，HDR视频为了存储更大范围的亮度使用HLG(Hybrid Log-Gamma混合对数)、PQ(Perceptual Quantization感知量化)，如下图所示就是Gamma、HLG、PQ曲线图。

元数据

HDR视频有四种格式，视频格式不同传递函数也不一样。

HDR视频	传递函数	元数据	位数
PQ10	PQ	ST-2084无元数据	10位
HDR10	PQ/HLG	ST-2086静态元数据	10位
HDR10+	PQ	ST-2094-40动态元数据	10位
Dolby Vision	PQ	ST-2094-10动态元数据	10位/12位

注意：

1. HDR视频播放时需要根据每一帧的亮度信息调整效果，但是亮度信息计算很慢不适合放在播放阶段，为了解决这个问题会在视频制作时就直接生成亮度信息，亮度信息就是所谓的元数据(metadata)。H265的元数据放在SEI/VUI中，解码时只要识别即可不影响原先的解码流程，又能直接利用元数据生成HDR效果。

2. 下图就是SEI(Supplemental Enhancement Information补充增强信息)中的元数据

   

   • display_primaries是色域三原色
   • white_point是白点
   • display_mastering_Luminance就是制作HDR视频的显示器亮度

3. 下图就是VUI(Video Usability Information视频可用信息)中的元数据。

   

   • colour_parimaries表明哪个色域
   • transfer_characteristics表明使用哪个传输函数
   • matrix_coeffs表明使用哪个YUV转RGB矩阵。

4. 按总体亮度还是每帧亮度又分为ST2086静态元数据和ST2094动态元数据(ST是电影电视工程师协会的英文缩写)，ST2094-10、ST2094-20、ST2094-30、ST2094-40分别对应杜比、飞利浦、特艺和三星四家公司。

5. 位深就是每个通道颜色的存储位数，SDR视频是8位，HDR视频10位/12位。

传递函数是怎么设计的

传递函数只要有Gamma函数就行了，为什么还要有HLG、PQ函数呢？因为Gamma只能产生1000的对比度(0.1-100的亮度)，HLG能产生20000的对比度(0.005-1000亮度)，PQ甚至产生2000000对比度(0.0005-10000亮度)。三个函数解决的问题不一样，Gamma函数解决8位的暗部细节问题，HLG函数既兼容Gamma函数又能处理10位数据，PQ函数能最大幅度利用10位或12位数据。

上图是网上找到的Gamma、HLG、PQ三条曲线，曲线可以自己动手用公式画出来。

亮度感知模型

那么为什么传递函数的曲线要这么设计呢？

不同的传递函数其实是根据不同的数学模型计算出来的，合适的传递函数需要考虑人眼对于亮度变化的察觉阈值(术语最小可觉差)，传递函数要与最小可觉差相贴合，不能太大也不能太小，太大会导致色阶断层，太小会浪费数据带宽。如果亮度用L表示，最小可觉差用△L表示，设计传递函数曲线其实就是找合适的$\frac{△L}{L}$曲线。

上图所有传递函数的曲线都用$\frac{△L}{L}$表示，横坐标是L，纵坐标是$\frac{△L}{L}$，曲线下方区域小于最小可觉差，曲线上方区域大于最小可觉差。

注意：

1. 根据韦伯费希纳定律，亮度感知是对数均匀，对应的编码方式就是Log编码，该编码对0-1000亮度适用，在$\frac{△L}{L}$图中是一条红色横线，而用物理亮度和视觉亮度关系表示就是下图，S-log是索尼相机的log曲线。

   

2. 根据史蒂文斯幂定律，亮度感知是立方根均匀，对应的编码方式就是Gamma编码，SDR视频用的传递函数就是Gammma编码，只不过因为屏幕绝对亮度不高选用平方根而不是立方根，该编码对0-100亮度更适用，在$\frac{△L}{L}$图中就是一条蓝色斜线。下图就是史蒂文斯幂定律测出来的值，其中点光源的幂指数0.5和BT709 Gamma使用的0.45很接近。
   

3. 根据Schreiber Curve定律(1992年Schreiber发现的规律)，亮度感知暗处是平方根均匀、明处是对数均匀，对应编码就是HLG编码，下方黄色曲线就是带HLG的$\frac{△L}{L}$图。
   
   HLG用物理亮度和视觉亮度关系表示就是下图，HLG前半部分贴合Gamma曲线后半部分是LOG曲线，这也是为什么HLG叫混合对数编码的原因。
   

4. 根据Barten Ramp视觉模型(1992年Barten发表的论文模型)，Baren Ramp曲线是人类最小可觉差模型，越贴合Baren Ramp曲线视觉越平滑，PQ曲线尽量贴合Baren ramp曲线，对应编码就是PQ函数，在$\frac{△L}{L}$图中是一条绿色曲线，用物理亮度和视觉亮度关系表示就是下图。

传递函数公式

传递函数的公式代码在zimg中可以看到,但是公式中的参数都不解释很容易一脸懵逼，为了尽可能地把公式解释清楚花了好几天查阅了各种资料，争取把每个参数是什么、参数是怎么设计考虑的都讲明白，没讲明白的参数欢迎大家在评论区讲解。
首先大家要先明白传递函数是为了转换线性光和非线性电，其中各种符号如下

1. $OETF$表示把自然场景的场景光$O$转换成电信号$E$
2. $OET{F}^{-}1$表示把电信号$E$转换成自然场景的场景光$O$
3. $OOTF$表示把自然场景的场景光$O$转换成屏幕的显示光$O$，$O$和$O$不一样，
4. $OOT{F}^{-}1$表示把屏幕的显示光$O$转换成自然场景的场景光$O$
5. $EOTF$表示把电信号$E$转换成屏幕的显示光$O$，该过程和$OETF$不是完全可逆的，中间会经过$OOTF$处理，即$EOTF=OET{F}^{-1}\ast OOTF$
6. $EOT{F}^{-}1$表示把屏幕的显示光$O$转换成电信号$E$

注意：

1. E代表电，O代表光。
2. O有两种，自然场景的场景光和屏幕的显示光，
3. 在转换过程中以场景光为基准叫场景参考，以显示光为参考叫显示参考。拍摄用时场景参考转换效果更好，编辑时用显示参考转换效果更好。

BT709 Gamma

BT709 Gamma函数一般都直接简化成了OETF$x^{0.45}$曲线或者EOTF$x^{2.2}$讲解，但是其实在亮度很小时Gamma函数其实是条直线，因为如果全部使用$x^{0.45}$曲线的话会丢失黑色阴影附近的值，如下图所示BT709 Gamma和Gamma2.2还是有一定区别的。

OETF

公式可视化

注意：

1. L就是场景光信号(范围$[0,1]$)，V就是电信号也就是非线性RGB(范围$[0,1]$)

2. 理论上$x^{0.45}$曲线也可以，但是屏幕反光会导致暗部细节丢失，需要把暗部变暗也就是曲线前半段往下拉。如果乘以小于1的系数会把整段曲线都往下拉，怎么解决呢？设系数为$\alpha$，曲线变成 $\alpha \ast x^{0.45}$，$x=1$时该曲线的值等于$\alpha$，$\alpha$小于1需要把$\alpha$变成$1$，很简单加上$1-\alpha$就行，公式从$x^{0.45}$变成了$\alpha \ast x^{0.45}+1-\alpha$

3. $\alpha \ast x^{0.45}+1-\alpha$曲线的前半段小于0，BT709把前半段曲线变成斜率为4.5的直线解决负数问题(斜率为什么选4.5没找到资料)，设前半段分界线$x$值等于$\beta$，那么公式变成了
   $$\{\begin{array}{rl}& 4.5\ast x,x<\beta ,直线\\ & \alpha \ast x^{0.45}+1-\alpha ，\beta <=x<=1,曲线\end{array}$$
   为了平滑上述公式中的两条线，列出以下方程
   $$\{\begin{array}{rl}& 4.5\ast \beta =\alpha \ast {\beta }^{0.45}+1-\alpha ，两条线连接处相等\\ & 4.5=0.45\ast \alpha \ast {\beta }^{-0.55}，两条线连接处的导数相等\end{array}$$

   最终算出$\alpha =1.099，\beta =0.018$，也就是前面公式值的由来。

4. 经过BT709处理过后的Gamma0.45反而更接近$x^{0.5}$。
   

EOTF

注意： 上述公式就是OETF的逆过程

HLG

HLG刚开始是英国BBC和日本NHK电视台为了让HDR视频兼容SDR屏幕提出来的ARIB STD-B67(ARIB是日本无线工业及商贸联合会英文缩写)，ITU(国际电联)把ARIB STD-B67纳入了BT2100标准，两个标准的公式实际是一样的只是做了换算。所谓HLG兼容SDR屏幕，不是指HDR视频能在SDR屏幕上播放，而是当屏幕兼容BT2020色域时屏幕亮度不够亮时自动根据屏幕亮度调整效果从而降低设备成本。

HLG只定义了OETF，EOTF是从OETF算出来的$OETF=OET{F}^{-1}\ast OOTF$，如下图所示在拍摄时用$OETF$把场景光信号压缩成电信号，播放时通过$EOT{F}^{-1}$逆转成场景光信号，场景光信号还要用$OOTF$变成屏幕光信号。

OETF

ARIB STD-B67

BT2100HLG

公式可视化

注意：

1. E是显示光信号也就是线性RGB，$E^{\prime }$就是电信号也就是非线性RGB

2. HLG公式分两部分，$\sqrt{E} $不就是$E^{0.5}$吗，这就是为什么说HLG前半部分曲线是Gamma函数的原因。$ln(E)$不就是$log_e(E)$吗，这就是为什么说HLG后半部分曲线是LOG函数的原因，其他r、a、b、c无非是调整曲线的幅度和偏移。

3. ARIB STD-B67的E范围是$[0,12]$，BT2100HLG的E范围是$[0,1]$，ARIB STD-B67的$r$取0.5再乘上范围12就变成BT2100HLG，范围取12表示动态范围扩大了12倍。

4. r=0.5表示BT2100HLG把50%的颜色定义成了SDR，这也是BT2100也叫做50%HLG的原因，在BT2408中把75%的颜色定义成了SDR也叫做75%HLG。注意50%HLG和75%HLG的公式没变，r还是0.5，只是100%SDR对应的亮度发生了变化，50%HLG的100%SDR所对应亮度是100nit，75%HLG的100%SDR所对应亮度是203nit。100%SDR分割了SDR和HDR也叫做参考白电平，参考白电平拍摄时作为曝光基准，播放时作为白色字幕的颜色。

5. $a=0.17883277$，$b=1-4a=0.28466892$，$ c= 0.5 - a* ln(4*a)=0.55991073$，这些值都是为了平滑连接HLG的两段曲线从以下方程算出来的
   $$\{\begin{array}{rl}\sqrt{3\ast E}& =a\ast ln(12\ast E-b)+c，E=\frac{1}{12}\\ \frac{\sqrt{3\ast E}}{dE}& =\frac{a\ast ln(12\ast E-b)+c}{dE}，E=\frac{1}{12}\\ E^{\prime }& =a\ast ln(12\ast E-b)+c，E=1，E^{\prime }=1\end{array}$$

   • 第一个等式表示两条线连接处相等
   • 第二个等式表示两条线连接处的导数相等。
   • 第三个等式表示曲线最右边的点

$OET{F}^{-1}$

注意： 上述公式就是EOTF的逆过程

OOTF

$$\begin{array}{rl}& F_D=\alpha Y_S^{\gamma -1}\ast E_S\\ & \gamma =1.2+0.42\ast lo{g}_{10}\frac{L_W}{1000}\end{array}$$

注意：

1. $F_D$ 和 $E_S$都是光信号，只是$F_D$表示显示光， $E_S$表示场景光，$Y_S$ 表示场景光RGB转换出的亮度，$L_W$为当前屏幕的最大亮度
2. HLG没有元数据能实现不同屏幕下的肤色看起来差不多就是因为上述公式中的$\gamma$是可变的，$\gamma$随着屏幕亮度变化，$Y_S^{\gamma -1}$又关联了视频亮度，最终HLG的相对亮度虽然没有PQ的绝对亮度那么精准但是够简单。屏幕亮度为1000时候$\gamma$是1.2，这是祖祖辈辈传下来的OOTF，因为SDR时代拍摄时使用BT709的OETF$\gamma$近似0.5，显示时用BT1886的EOTF$\gamma$等于2.4，自然OOTF就是$0.5\ast 2.4=1.2$。
3. $\alpha$用于自定义调整强度。

EOTF

$$\begin{array}{rl}& F_D=OOTF[OET{F}^{-1}[max(0,(1-\beta )\ast E^{\prime }+\beta )]]\\ & \beta =\sqrt{3\ast (\frac{L_B}{L_W}{)}^{\frac{1}{\gamma }}}\end{array}$$

注意：

1. $F_D$表示显示光信号也就是线性RGB，$E^{\prime }$就是电信号也就是非线性RGB
2. $\beta$用来增大黑电平(定义什么颜色算是黑色)，$L_B$表示黑电平的亮度也就是当前屏幕的最小亮度，$L_W$表示白电平(定义什么颜色算是白色)的亮度也就是当前屏幕的最大亮度

PQ

PQ只定义了EOTF，OETF是从EOTF算出来的$OETF=OOTF\ast EOT{F}^{-1}$，如下图所示在拍摄时先用OETF先把场景信号编码成电信号，显示时用$EOTF$解码成显示光信号。注意观察PQ的OOTF在拍摄环节而HLG的OOTF在显示环节，个人感觉之所以不一样是因为PQ是绝对亮度体系对于亮度的处理当然要在拍摄时处理保证和屏幕无关、HLG是相对亮度体系对于亮度的处理要在显示时根据屏幕的亮度而变化。

EOTF

$$\begin{array}{rl}& F_D=10000{\left(\frac{max[(E^{\prime \frac{1}{m_2}}-c_1),0]}{c2-c3\ast E^{\prime \frac{1}{m_2}}}\right)}^{\frac{1}{m_1}}\end{array}$$

公式可视化

注意：

1. $F_D$表示显示光信号也就是线性RGB，$E^{\prime }$就是电信号也就是非线性RGB
2. PQ分割SDR和HDR的界限是58%，这也是PQ又叫做58%PQ的原因，58%PQ所对应的亮度也是203nit。
3. PQ公式的参数是怎么算出来的没找到资料，只知道和Barten Ramp模型的公式有关。

$$\begin{array}{rl}& m_1=\frac{2610}{16384}=\frac{1305}{8192}=0.1593017578125\\ & m_2=128\frac{2523}{4096}=\frac{2523}{32}=78.84375\\ & c_1=\frac{3424}{4096}=\frac{107}{128}=0.8359375=c_3-c_2+1\\ & c_2=32\frac{2413}{4096}=\frac{2413}{128}=18.8515625\\ & c_3=32\frac{2392}{4096}=\frac{2392}{128}=18.6875\end{array}$$

$EOT{F}^{-1}$

$$\begin{array}{rl}& E^{\prime }={\left(\frac{c1+c2\ast Y^{m1}}{1+c3\ast Y^{m1}}\right)}^{m2}\end{array}$$

注意： 上述公式就是EOTF的逆过程

OOTF

$$\begin{array}{rl}& F_D=OOTF[E]=G_{1886}[G_{709}[E]]\\ & E^{\prime }=G_{709}[E]=\{\begin{array}{rl}& 267.84E,E<=0.0003024\\ & 1.099(59.5208E{)}^{0.45}-0.099,E>0.0003024\end{array}\\ & F_D=G_{1886}=100E^{\prime 2.4}\end{array}$$

注意：

1. $F_D$和$E$都是光信号，只是$F_D$表示场景光， $E$表示显示光

2. PQ的OOTF其实是模拟BT1886色域的屏幕显示BT709的过程，个人感觉是为了兼容以前的SDR信号。

3. $G_{709}$和BT709的OETF是一样的，只是让E乘上了59.5208($59.5208\ast 4.5=267.84，0.0003024\ast 59.5208=0.018$)，之所以乘这个数按BT2039的说法它代表了HDR相对于SDR的扩展比例, 如下图所示就是BT2039中的描述，59.5208是从BT709的OETF和BT1886的EOTF中算出来的
   
   说直白点就是下方曲线中Y=100(Y=1表示100亮度，Y=100表示10000亮度)时X是59.5208
   

4. $G_{1886}$和BT1886的EOTF是一样的都是Gamma2.4，只是乘以100，之所以乘以100是因为PQ的最大亮度是10000而BT1886的最大亮度是100，10000/100=100是为了放大范围。

OETF

$$\begin{array}{rl}& E^{\prime }=OETF[E]=EOT{F}^{-1}[OOTF[E]]\end{array}$$

注意： $E$表示显示光信号也就是线性RGB，$E^{\prime }$就是电信号也就是非线性RGB

问题思考

下面2个问题留给大家思考

1. PQ公式中的值是怎么从Barten Ramp视觉模型算出来的
2. BT709的Gamma函数前半部分直线斜率4.5是根据什么决定的

系列文章

• HDR转SDR实践之旅(一)流程总结
• HDR转SDR实践之旅(二)解码10位YUV纹理
• HDR转SDR实践之旅(三)YUV420转YUV公式
• HDR转SDR实践之旅(四)YUV转RGB矩阵推导
• HDR转SDR实践之旅(五)色域转换BT2020转BT709
• HDR转SDR实践之旅(六)传递函数与色差矫正
• HDR转SDR实践之旅(七)Gamma、HLG、PQ公式详解
• HDR转SDR实践之旅(八)色调映射
• HDR转SDR实践之旅(九)HDR开发资源汇总
• HDR转SDR实践之旅(十)SDR转HDR逆色调映射探索